Eksamen høst 2025

Innhold

Eksamen høst 2025#

Del 1 – Uten hjelpemidler#

Oppgave 1 (2 poeng)

Løs ulikheten

\[ x^2 + 4x - 5 < 0 \]

Fasit

\[ x \in \langle -5, 1 \rangle. \]

Løsning

Vi starter med å bestemme nullpunktene til \(f(x) = x^2 + 4x - 5\). Vi bruker \(abc\)-formelen:

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-4 \pm \sqrt{16 + 20}}{2} = \frac{-4 \pm \sqrt{36}}{2} = \frac{-4 \pm 6}{2} \]

Dette gir oss to nullpunkter:

\[ x = -5 \or x = 1 \]

Det betyr at vi kan skrive om uttrykket til nullpunktsform slik at ulikheten blir

\[ (x + 5)(x - 1) < 0 \]

Grafen til uttrykket vil være konveks smile polynomial icon siden den ledende koeffisienten er positiv. Da må grafen ligge under \(x\)-aksen mellom nullpunktene som betyr at løsningen på ulikheten er

\[ x \in \langle -5, 1 \rangle. \]

Oppgave 2 (3 poeng)

Bestem nullpunktene til funksjonen \(f\) gitt ved

\[ f(x) = x^3 - 5x^2 - 8x + 12 \]

Fasit

\[ x = -2 \or x = 1 \or x = 6 \]

Løsning

De mulige heltallige nullpunktene til \(f\) vil være \(x\)-verdier som kan dele konstantleddet \(12\). De betyr at mulige nullpunkter er

\[ x \in \{\pm 1, \pm 2, \pm 3, \pm 4, \pm 6, \pm 12\} \]

Vi tester ut verdiene systematisk til vi treffer et nullpunkt. Vi bruker et Horner-skjema:

Vi ser at vi får \(0\) i rest som betyr at \(x = 1\) er et nullpunkt. Fra Horner-skjemaet kan vi også lese av resultatet av polynomdivisjonen \(f(x) : (x - 1)\) som er:

\[ f(x) : (x - 1) = x^2 - 4x - 12 \liff f(x) = (x - 1)(x^2 - 4x - 12) \]

For å bestemme de resterene nullpunktene, må vi løse likningen

\[ x^2 - 4x - 12 = 0 \]

Vi bruker \(abc\)-formelen:

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{4 \pm \sqrt{16 + 48}}{2} = \frac{4 \pm \sqrt{64}}{2} = \frac{4 \pm 8}{2} \]

Dette gir oss to nullpunkter:

\[ x = 6 \or x = -2 \]

Altså er nullpunktene til funksjonen \(f\):

\[ x = -2 \or x = 1 \or x = 6 \]

Oppgave 3 (4 poeng)

En rasjonal funksjon \(f\) er gitt ved

\[ f(x) = \dfrac{2x + 6}{x^2 + 4} \]

Påstand 1: Grafen til \(f\) har nøyaktig ett nullpunkt.
Påstand 2: Grafen til \(f\) har ingen vertikale asymptoter.
Påstand 3: Grafen til \(f\) skjærer aldri \(y\)-aksen
Påstand 4: Grafen til \(f\) har en horisontal asymptote \(y = 2\).

Fasit

Påstand 1: Sann
Påstand 2: Sann
Påstand 3: Usann
Påstand 4: Usann

Løsning

Påstand 1: Grafen til \(f\) har nøyaktig ett nullpunkt siden telleren er en lineær funksjon og denne har ett nullpunkt. Nevnerpolynomet har ingen nullpunkter så vi trenger ikke bekymre oss for at både teller og nevneren er null samtidig. Dermed er påstanden sann.
Påstand 2: Grafen til \(f\) har ingen vertikale asymptoter siden nevnerpolynomet ikke har noen nullpunkter. Påstanden er derfor sann.
Påstand 3: Grafen \(f\) skjærer \(y\)-aksen siden uttrykket er definert for \(x = 0\). Påstanden er derfor usann.
Påstand 4: Nevnergraden er høyere enn tellergraden som betyr at den horisontale asymptoten må være \(y = 0\). Påstanden er derfor usann.

Oppgave 4 (2 poeng)

For fem år siden vant Oskar i Lotto. Han satte pengene i banken og har fått \(4.5~\%\) rente per år. I dag har han \(250~000\) kroner på kontoen.

Hvilket eller hvilke av uttrykkene nedenfor kan vi bruke for å regne ut hvor mye Oskar vant i Lotto?

\[ 250~000 \cdot (0.955)^5 \]

\[ \dfrac{250~000}{1.045^5} \]

\[ 250~000 \cdot 1.045^5 \]

\[ 250~000 \cdot 0.955^{-5} \]

\[ \dfrac{250~000}{0.955^5} \]

\[ 250~000 \cdot 1.045^{-5} \]

Fasit

Uttrykk 2 og 6.

Løsning

I dag er verdien \(250~000\) og den har økt med \(4.5~\%\) per år som tilsvarer en vekstfaktor på \(1.045\). Det betyr at pengene på kontoen er beskrevet av eksponentialfunksjonen

\[ f(x) = a \cdot 1.045^x \]

der \(a\) er startverdien (det Oskar vant i Lotto) og \(x\) er antall år pengene har stått i banken. Etter \(5\) år (som er i dag) så er \(f(5) = 250~000\). For å finne \(a\) må vi løse likningen

\[ f(5) = a \cdot 1.045^5 = 250~000 \liff a = \dfrac{250~000}{1.045^5} \]

Dette kan også skrives om til

\[ a = 250~000 \cdot 1.045^{-5} \]

Altså er både uttrykk 2 og 6 riktige.

Oppgave 5 (5 poeng)

a

Bruk trekanten ovenfor til å vise at \(\sin 45\degree = \dfrac{1}{\sqrt{2}}\)

Løsning

Trekanten er en likesidet trekant som betyr at de to andre vinklene er \(45 \degree\). Definisjonen av sinus gir da:

\[ \sin 45\degree = \dfrac{\text{motstående katet}}{\text{hypotenus}} = \dfrac{1}{\sqrt{1^2 + 1^2}} = \dfrac{1}{\sqrt{2}} \]

b

Gitt en trekant \(ABC\) der \(AB = 3\sqrt{2}\), \(AC = 8\) og \(\angle A = 45\degree\).

Bestem arealet av trekanten.

Fasit

\[ T = 12. \]

Løsning

Arealsetningen gir oss

\[ T = \dfrac{1}{2}AB\cdot AC \cdot \sin 45\degree = \dfrac{1}{2}\cdot 3\sqrt{2} \cdot 8 \cdot \dfrac{1}{\sqrt{2}} = 12 \]

c

Gitt en trekant \(PQR\) der \(PQ = 3\sqrt{2}\), \(PR = 8\) og \(\angle P = 140\degree\).

Hvilken av trekantene \(ABC\) og \(PQR\) har størst areal?

Husk å argumentere for svaret ditt.

Fasit

Trekant ABC har størst areal.

Løsning

Fra arealsetningen vil

\[ T_{PQR} = \dfrac{1}{2} PQ \cdot PR \cdot \sin \angle P \]

Siden \(PQ = AB\) og \(PR = AC\), må vi bare sammenligne \(\sin \angle A\) og \(\sin \angle P\). Vi har at

\[ \sin \angle P = \sin 140\degree = \sin (180\degree - 140\degree) = \sin 40 \degree. \]

Fra enhetssirkelen vet vi at \(\sin x\degree\) øker når \(x\) øker og \(x \in \langle 0, 90\rangle\). Det betyr at \(\sin 45\degree > \sin 140\degree\). Altså må arealet til trekant \(ABC\) være størst.

Oppgave 6 (3 poeng)

Siri arbeider med femkanttall. Hun har oppdaget en sammenheng og laget programmet nedenfor.

tall = 1
differanse = 4

while tall <= 60:
    print(tall)
    tall = tall + differanse
    differanse = differanse + 3

Hvilke tall vil bli skrevet ut når programmet kjøres?

Gjør rede for sammenhengen Siri har oppdaget.

Løsning

La \(F_n\) være femkanttall \(n\) (figur \(n\)). Da har vi

\[ F_1 = 1 \and F_2 = 5 \and F_3 = 12 \and F_4 = 22 \]

Sammenhengen Siri har oppdaget er at

\[ F_{n + 1} = F_n + d_n \]

der \(d_n\) er differansen mellom figur \(n\) og figur \(n + 1\) som tilfredsstiller

\[ d_{n + 1} = d_n + 3 \]

Programmet vil skrive ut \(F_n\) så lenge \(F_n \leq 60\). Vi må derfor regne ut \(F_n\) med sammenhengene ovenfor frem til vi finner at \(F_n > 60\).

Vi må vite verdien til \(d_5\). Vi har at \(d_1 = 4\). Da får vi at

\[\begin{split} \begin{align*} d_2 &= d_1 + 3 = 4 + 3 = 7 \\ \\ d_3 &= d_2 + 3 = 7 + 3 = 10 \\ \\ d_4 &= d_3 + 3 = 10 + 3 = 13 \\ \\ d_5 &= d_4 + 3 = 13 + 3 = 16 \\ \end{align*} \end{split}\]

Nå kan vi regne ut \(F_5\):

\[ F_5 = F_4 + d_4 = 22 + 13 = 35 \]

Videre regner vi ut \(d_6\) og \(F_6\):

\[\begin{split} \begin{align*} d_6 &= d_5 + 3 = 16 + 3 = 19 \\ \\ F_6 &= F_5 + d_5 = 35 + 16 = 51 \\ \end{align*} \end{split}\]

\(F_7\) må nødvendigvis være større enn \(60\) siden \(d_6 = 19\). Dermed vil programmet skrive ut tallene

\[ 1, 5, 12, 22, 35, 51 \]

Del 2 – Med hjelpemidler#

Oppgave 1 (8 poeng)

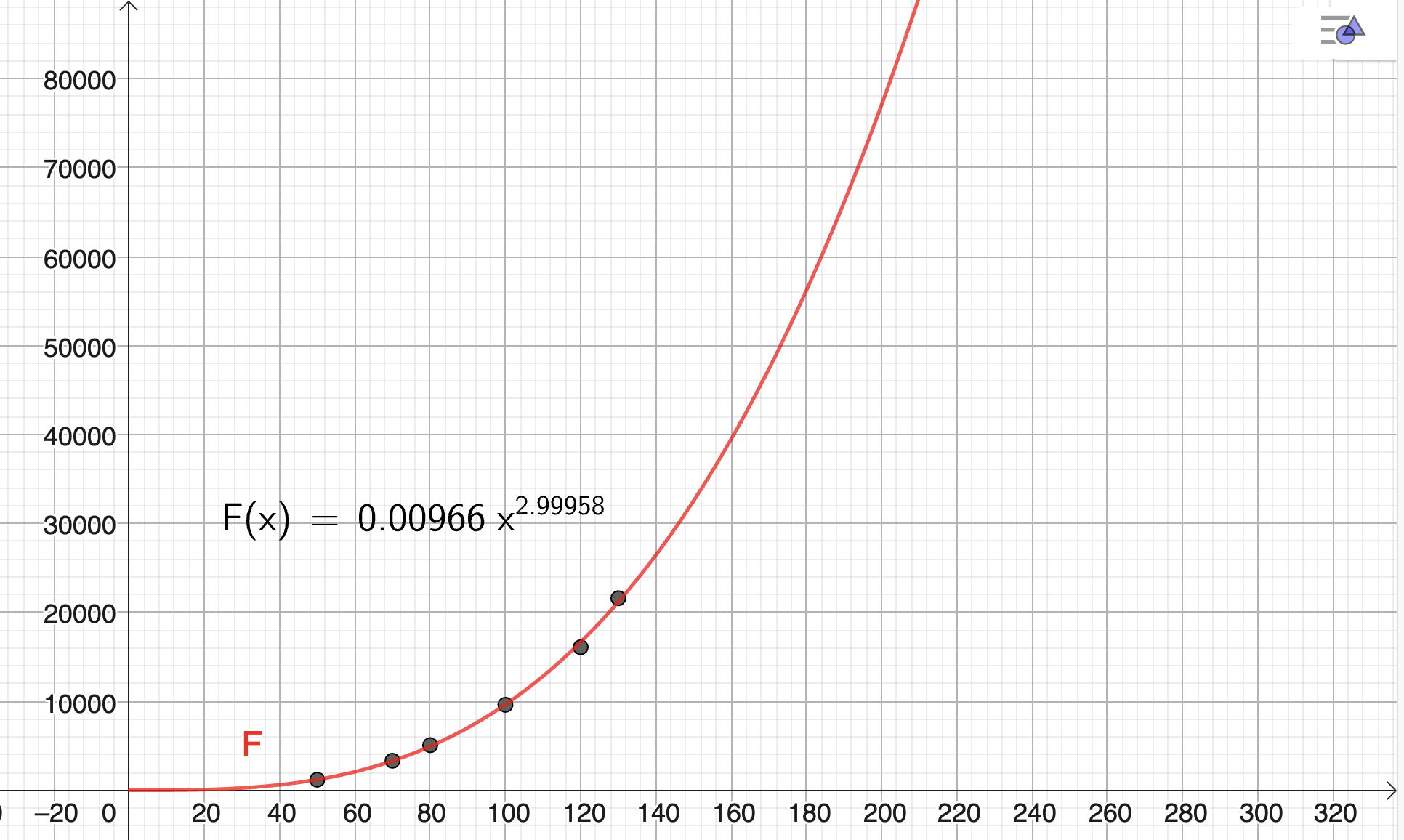
Tabellen nedenfor viser sammenhengen mellom lengde og vekt på en type fisk.

Lengde (cm)	\(50\)	\(70\)	\(80\)	\(100\)	\(120\)	\(130\)
Vekt (gram)	\(1190\)	\(3320\)	\(5070\)	\(9610\)	\(16~080\)	\(21~590\)

Sammenhengen kan beskrives med en modell \(F\) gitt på formen

\[ F(x) = a \cdot x^b \]

der \(F(x)\) gram er vekten til en fisk som er \(x\) centimeter lang.

a

Bruk opplysningene i tabellen til å bestemme tallene \(a\) og \(b\).

Tegn grafen til \(F\).

Løsning

Vi bestemmer modellen \(F(x)\) med regresjon og bruker en potensfunksjon som modell:

Altså er

\[ a \approx 0.00966 \and b \approx 2.99 \]

Grafen til \(F\) ser da slik ut:

Her viser \(x\)-aksen lengden til fisken i cm og \(y\)-aksen viser vekten i gram.

b

Bestem stigningstallet til den rette linjen som går gjennom punktene \((75, F(75))\) og \((95, F(95))\).

Gi en praktisk tolkning av svaret.

Løsning

Stigningstallet til den rette linja gjennom de to punktene er den gjennomsnittlige vekstfarten til \(F\) på intervallet \([75, 95]\). Vi regner ut med CAS:

Altså er stigningstallet til linja ca. \(210\) gram/cm. Det betyr vekten til fisketypen i gjennomsnitt med 210 gram for hver centimeter lengden øker på intervallet \([75, 95]\) cm.

c

Bestem den momentane vekstfarten når \(x = 100\).

Gi en praktisk tolkning av svaret.

Løsning

Den momentane vekstfarten når \(x = 100\) er \(F'(100)\). Vi regner ut med CAS:

d

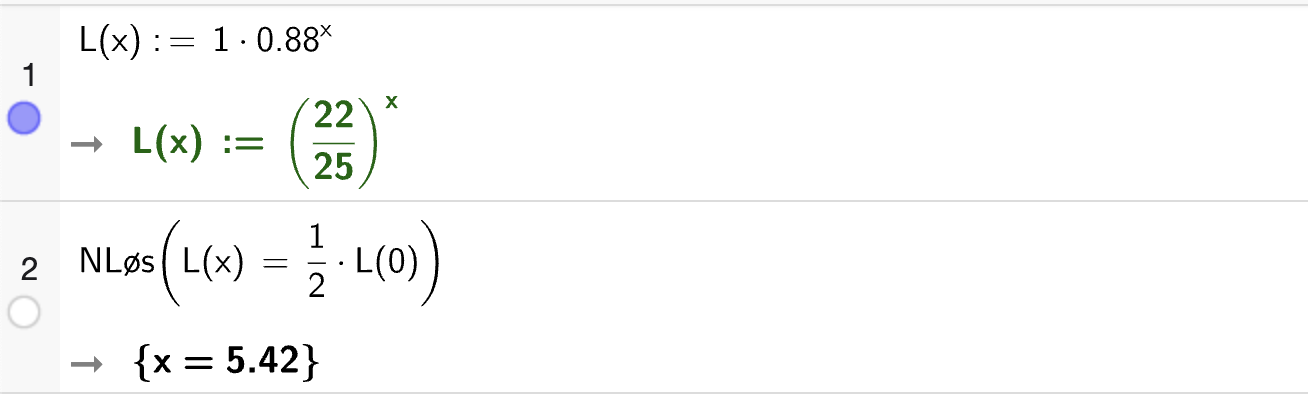
Hvor mange prosent vil vekten til en fisk øke med dersom lengden øker med \(20~\%\) ifølge modellen?

Oppgave 2 (2 poeng)

I dag er Abid, Therese og Harald til sammen \(68\) år. Therese er \(17\) år eldre enn Abid.

Om tre år vil Abid være dobbelt så gammel som Harald.

Hvor gamle er Abid, Therese og Harald i dag?

Løsning

Vi lar \(A\) være alderen til Abid, \(T\) være alderen til Therese og \(H\) være alderen til Harald i dag.

Siden de til sammen er 68 år, har vi at

\[ A + T + H = 68 \]

Therese er 17 år eldre enn Abid i dag som betyr at

\[ T = A + 17 \]

Om tre år vil Abid være dobbelt så gammel som Harald, som vi kan beskrive med likningen

\[ A + 3 = 2(H + 3) \]

Vi løser likningssystemet med CAS:

Altså er Abid \(21\) år gammel, Harald er \(9\) år gammel og Therese er \(38\) år gammel i dag.

Oppgave 3 (5 poeng)

Gitt figuren ovenfor.

a

Gjør beregninger og vis at \(AC = 3\).

Løsning

La \(x = AC\). Vi bruker sinussetningen for å bestemme sidelengden med CAS:

Altså er \(AC = 3\).

b

Bestem arealet av firkanten \(ABCD\).

Gi svaret eksakt.

Fasit

\[ T_{\square ABCD} = \dfrac{3}{4}\left(2\sqrt{3} + 3\right) \]

Løsning

Firkanten \(ABCD\) er består av to trekanter \(\triangle ABC\) og \(\triangle ACD\).

Arealet av \(\triangle ACD\) kan vi bestemme direkte med arealsetningen:

\[ T_{\triangle ACD} = \dfrac{1}{2}\cdot AC \cdot CD \cdot \sin 30\degree \]

Vi regner ut med CAS:

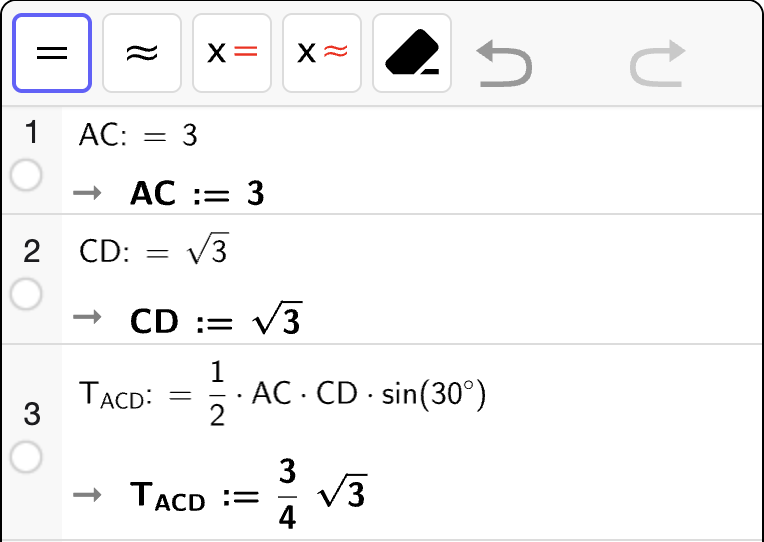
Altså er \(T_{\triangle ACD} = \dfrac{3\sqrt{3}}{4}\).

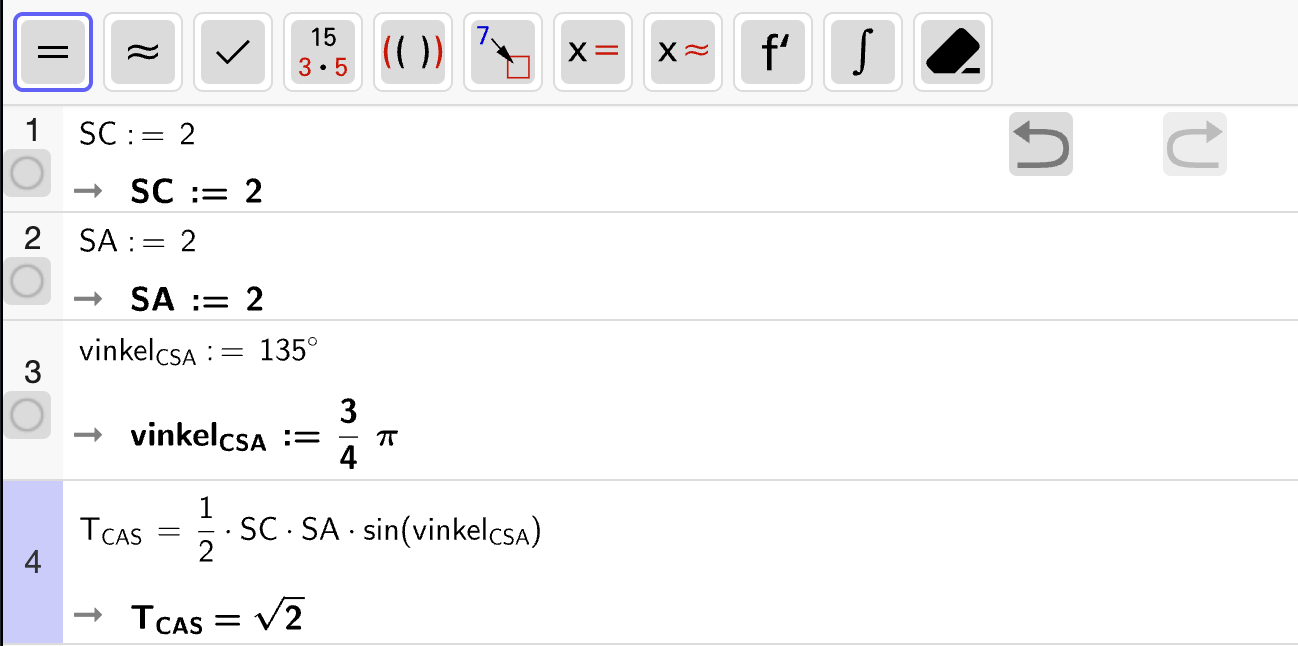
For å bestemme arealet av \(\triangle ABC\) bruker vi også arealsetningen. Her velger vi å ta utgangspunkt i vinkelen \(\angle BAC = 45\degree\) som vil gi

\[ T_{\triangle ABC} = \dfrac{1}{2} \cdot AB \cdot AC \cdot \sin 45\degree \]

Vi kjenner ikke til \(AB\), men den kan vi bestemme ved hjelp av cosinussetningen med utgangspunkt i vinkelen \(\angle BAC\) som gir

\[ BC^2 = AC^2 + AB^2 - 2 \cdot AC \cdot AB \cdot \cos 45\degree \]

Vi bruker CAS til å bestemme \(AB\). La \(x = AB\).

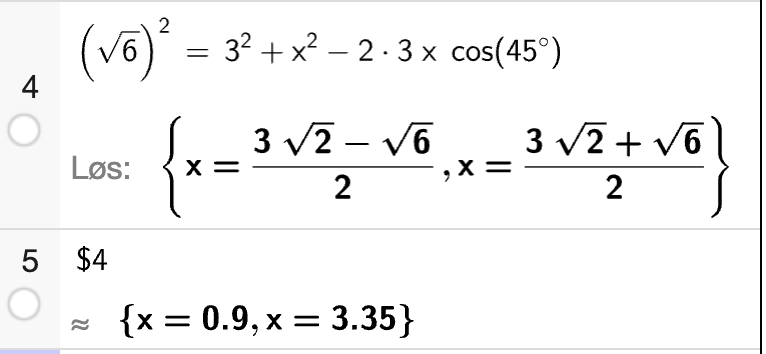
Sidelengden \(AB\) er lenger enn \(AC\), så vi må velge den største løsningen. Altså er

\[ AB = \dfrac{3 \sqrt{2} + \sqrt{6}}{2} \]

Så regner vi ut arealet av \(\triangle ABC\) med CAS:

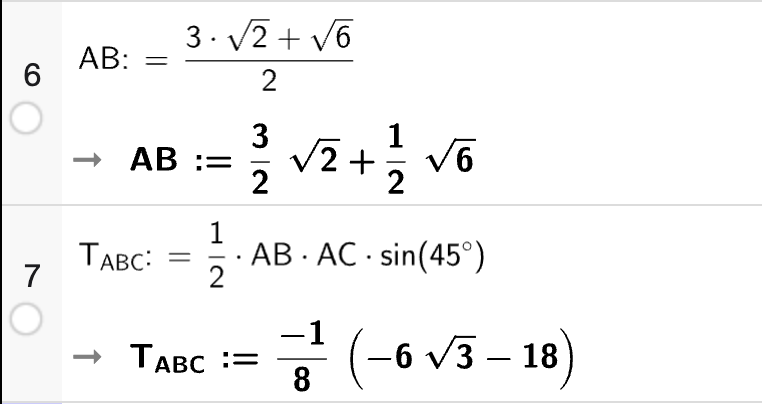
Så legger vi sammen de to arealene for å få det eksakte arealet av firkanten \(ABCD\):

Dermed er det eksakte arealet av firkanten \(ABCD\) gitt ved

\[ T_{\square ABCD} = \dfrac{3}{4}\left(2\sqrt{3} + 3\right) \]

Oppgave 4 (3 poeng)

Maria tegner en likesidet trekant. Hun deler trekanten i flere og flere små likesidene trekanter og fargelegger et mønster. Figurene nedenfor viser hvordan hun arbeider.

Tenk deg at Maria fortsetter å dele opp trekanten og fargelegge etter samme mønster.

a

Sett opp en algoritme Maria kan bruke for å finne summen av arealene av de 100 første trekantene som vil være fargelagte.

Løsning

La \(T\) være arealet av hele trekanten. Den første fargelagte trekanten vil ha \(1/3\) av grunnlinja og \(1/3\) av høyden til den opprinnelige trekanten. Det betyr at arealet blir \(1/9\) av arealet til \(T\). Den neste fargelagte trekanten vil ha \(1/9\) av dette arealet igjen. La \(T_n\) være arealet av den \(n\)-te fargelagte trekanten. Da har vi at

\[ T_{n + 1} = \dfrac{1}{9} T_n \]

Da kan vi lage følgende algoritme:

Sett arealet \(T\).
Sett summen av arealene til \(0\).
For \(n = 1, 2, \ldots, 100\):
1. Beregn \(T_{n} = \dfrac{1}{9}\cdot T_{n - 1}\).
2. Legg \(T_n\) til summen av arealene.

b

Ta utgangspunkt i algoritmen og lag et program som regner ut summen av arealene dersom arealet av den likesidete trekanten hun starter med er \(36\).

Løsning

areal_sum = 0

areal = 36 # Arealet til den store trekanten
for n in range(1, 101):
    areal = 1/9 * areal # Arealet av den fargelagte trekanten
    areal_sum = areal_sum + areal # summerer opp arealene
    
print(areal_sum)

som gir utskriften

4.5

som betyr at summen av arealene av de 100 første trekantene er \(4.5\).

Oppgave 5 (4 poeng)

Funksjonen \(f\) er gitt ved

\[ f(x) = \dfrac{10}{x^2 + 3} \qfor x > 0 \]

Punktene \(A\), \(B\), \(C\) og \(D\) danner et rektangel. Punktet \(A\) ligger i origi, punktet \(B\) ligger på \(x\)-aksen, punktet \(C\) ligger på grafen til \(f\), og punktet \(D\) ligger på \(y\)-aksen. Se figuren nedenfor.

a

Bestem arealet av rektangelet dersom punktet \(B\) har koordinatene \((3, 0)\).

Fasit

\[ \dfrac{5}{2} \]

Løsning

Arealet av rektangelet når \(B = (x, 0)\) vil være

\[ A(x) = xf(x) \]

Vi skal regne ut \(A(3)\) som vi gjør med CAS:

Altså er arealet av rektangelet når \(B = (3, 0)\) lik \(\dfrac{5}{2}\).

b

Hvor på \(x\)-aksen må punktet \(B\) ligge for at arealet av rektangelet \(ABCD\) skal bli størst mulig?

Fasit

\[ x = \sqrt{3} \]

Løsning

Tegner vi grafen til \(A(x)\) får vi

Grafen har et toppunkt i intervallet \([1, 2]\). Vi bestemmer \(x\)-koordinaten til dette toppunkt ved å løse \(A'(x) = 0\):

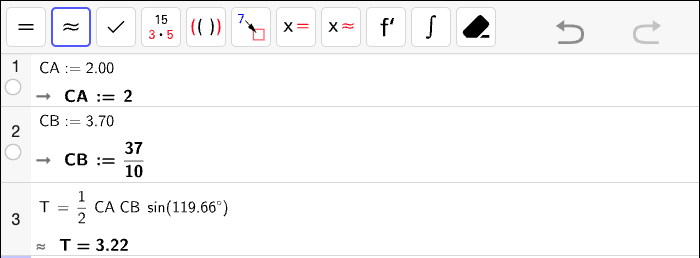
Altså er \(A(x)\) størst mulig dersom \(x = \sqrt{3}\). Dette er punktet på \(x\)-aksen der vi må plassere punktet \(B\) for at arealet av rektangelet skal bli størst mulig.

Oppgave 6 (3 poeng)

En arkitekt har tegnet et snitt av en lagerhall. Lagerhallen er 20 meter høy og har form som en parabel gitt ved

\[ p(x) = -\dfrac{1}{12}x^2 + 20 \]

På taket av lagerhallen skal det plasseres et webkamera. Webkameraet skal festet på en stang som er 3 meter lang.

Den rette linjen på figuren går gjennom punktet \((0, 23)\) og er en tangent til grafen.

a

Bestem likningen til tangenten.

Fasit

\[ y = -x + 23 \]

b

Hvor langt fra veggen på lagerhallen kan en tyv bevege seg uten å bli fotografert av webkameraet?

Fasit

Ca. 5.5 meter dersom en person er 2 meter høy.