Arealsetningen

Innhold

28. Arealsetningen#

Læringsmål

Kunne bruke arealsetningen til arealberegninger for trekanter.
Kunne begrunne arealsetningen.
Kunne bestemme \(\sin v\) for vinkler \(v \in \langle 0\degree, 180\degree\rangle\).

Repetisjon: Arealet av en trekant#

Fra geometri har du tidligere lært en måte å regne ut arealet av en trekant.

Arealet av en trekant

Arealet \(T\) av en trekant med grunnlinje \(g\) og høyde \(h\) er gitt ved

\[ T = \dfrac{g\cdot h}{2} \]

Dette stemmer både om vinkelene er spisse (\(<90\degree\)) eller om trekanten har en vinkel som er stump (\(>90\degree\)). Se figuren nedenfor.

Underveisoppgave 1

En trekant \(\triangle ABC\) er vist i figuren nedenfor. \(AB = 4\).

Bestem arealet av trekanten.

Fasit

\[ T = 2. \]

Løsning

Fra figuren, kan vi se at grunnlinja er \(g = AB = 4\) og høyden er \(h = 1\). Dermed blir arealet av trekanten

\[ T = \dfrac{g \cdot h}{2} = \dfrac{4 \cdot 1}{2} = 2. \]

Supplementvinkler#

Vi trenger et nytt begrep for å beskrive sammenhengen mellom to vinkler.

Supplementvinkler

Supplementvinkler: To vinkler \(u\) og \(v\) er supplementvinkler dersom \(u + v = 180\degree\).

Arealsetningen#

Arealsetningen lar oss regne ut arealet så lenge vi kjenner til to sidelenger og vinkelen som disse sidene spenner ut.

Arealsetningen

Arealet av en trekant er produktet av to sidelenger ganget med sinus til vinkelen som er spent ut av sidene, delt på 2. Vi kan dermed regne ut arealet \(T\) på tre forskjellige måter:

\[\begin{align*} T &= \dfrac{1}{2} \cdot AB \cdot AC \cdot \sin \angle A \\ \\ T &= \dfrac{1}{2} \cdot BA \cdot BC \cdot \sin \angle B \\ \\ T &= \dfrac{1}{2} \cdot CA \cdot CB \cdot \sin \angle C \end{align*}\]

Se figuren nedenfor.

Underveisoppgave 2

Nedenfor vises en trekant \(\triangle ABC\).

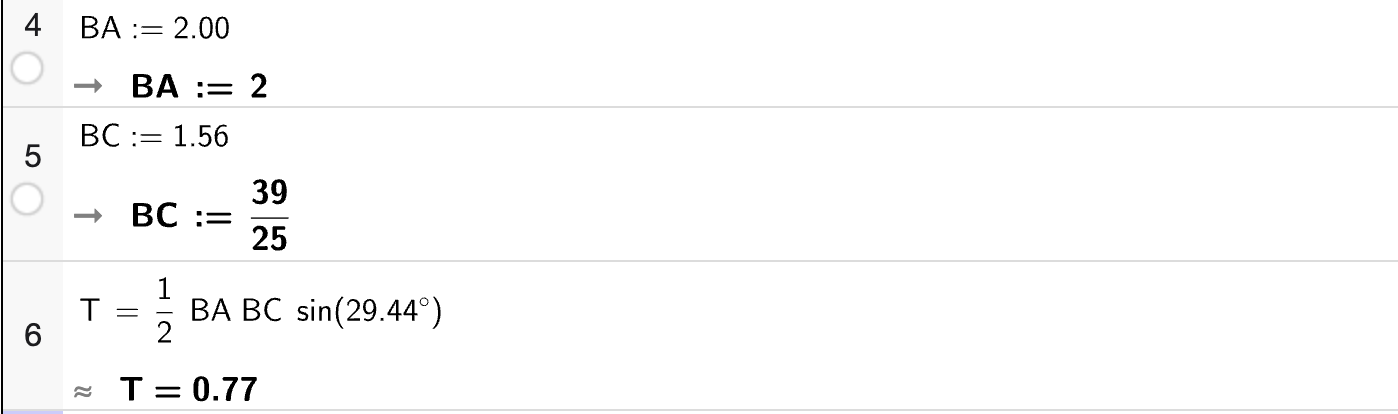
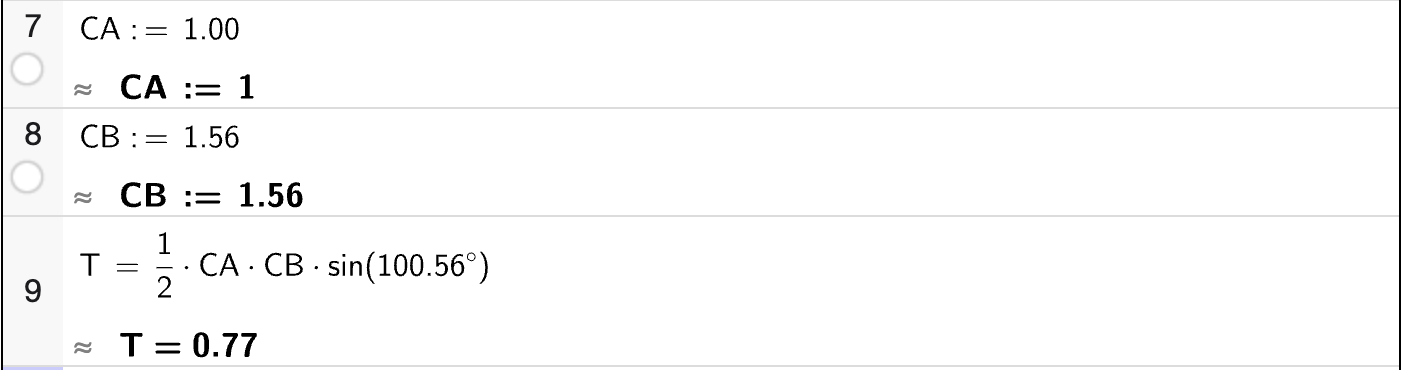
I CAS-vinduet nedenfor vises én måte å bruke arealsetningen på for å bestemme arealet av trekanten.
Bestem arealet på de to andre måtene som arealsetningen gir.

Løsning

Går vi ut ifra \(\angle B\), får vi:

\[ T = \dfrac{1}{2} \cdot BA \cdot BC \cdot \sin \angle B, \]

som vi kan regne ut med CAS:

Går vi ut ifra \(\angle C\), får vi:

\[ T = \dfrac{1}{2} \cdot CA \cdot CB \cdot \sin \angle C, \]

som gir

Arealet av trekanten er altså

\[ T \approx 0.77. \]

I Underveisoppgave 2 kan det hende du stusset litt over at vi kan regne ut \(\sin v\) når vinkelen \(v > 90\degree\). Vi har jo så langt bare definert \(\sin v\) ved hjelp av rettvinklede trekanter, og der finnes det ingen stumpe vinkler. Så det er naturlig å lure på hvordan dette gir mening.

Vi skal i det som følger både begrunne arealsetningen og gi mening til hva det vil si å regne ut \(\sin v\) når \(v > 90\degree\) så vi får tatt knekken på det mentale ubehaget. Du skal få begrunne setningen ut ifra en spiss vinkel først. Deretter skal vi utforske hva som skjer når vi går ut ifra en vinkel som er stump.

Utforsk 1

Nedenfor vises en trekant \(\triangle ABC\) med en spiss vinkel \(\angle A\), en høyde \(h\) og en grunnlinje \(g\).

a

Uttrykk grunnlinjen \(g\) ved hjelp av én av sidelengdene \(AB\), \(AC\) eller \(BC\).

Fasit

\[ g = AB \]

b

Bestem \(\sin \angle A\) uttrykt ved hjelp av én eller flere av lengdene \(AB\), \(AC\), \(BC\) og \(h\).

Fasit

\[ \sin \angle A = \dfrac{h}{AC} \]

c

Bestem en formel for \(h\) ut ifra svaret ditt fra b.

Fasit

\[ h = AC \cdot \sin \angle A \]

d

Bestem en formel for arealet \(T\) av trekanten ut ifra det du har funnet i a, b og c uttrykt med \(\sin \angle A\).

Fasit

\[ T = \dfrac{1}{2} g \cdot h = \dfrac{1}{2} \cdot AB \cdot AC \cdot \sin \angle A \]

siden \(g = AB\) og \(h = AC \cdot \sin \angle A\).

Nå har vi begrunnet hvorfor arealsetningen stemmer når vi tar utgangspunkt i en spiss vinkel. Nå skal vi undersøke hvordan vi kan forstå arealsetningen når vi tar utgangspunkt i en stump vinkel. Måten vi skal forstå \(\sin v\) når \(v\) er stump, er at vi bestemmer sinus til vinkelen vi får ved å danne en rettvinklet trekant på utsiden av trekanten.

Utforsk 2

Nedenfor vises en trekant \(\triangle ABC\) med en stump vinkel \(\angle A\), en høyde \(h\) og en grunnlinje \(g\).

a

Bestem grunnlinja \(g\) uttrykt ved hjelp av én av sidelengdene \(AB\), \(AC\) eller \(BC\).

Fasit

\[ g = AB \]

b

Bestem høyden \(h\) uttrykt ved hjelp av sidelenger i \(\triangle ABC\) og vinkel \(v\).

Fasit

\[ h = AC \cdot \sin (180\degree - v) \]

c

Bestem arealet \(T\) av trekanten ut ifra det du har funnet i a og b.

Fasit

\[ T = \dfrac{1}{2}\cdot AB \cdot AC \cdot \sin (180\degree - v) \]

Ut ifra resultatet i c Utforsk 2, så ser vi at det er rimelig å definere \(\sin v\) for en stump vinkel som at

\[ \sin v = \sin (180\degree - v). \]

Dette valget gjør at vi kan bruke arealsetningen med alle vinkler \(v\degree \in \langle 0, 180\rangle\).

Det vi mener med dette er at dersom vi skal regne ut \(\sin v\) til en stump vinkel på innsiden av en trekant, så gjør vi det ved å danne en rettvinklet trekant på utsiden og bruker supplementvinkelen \(180\degree - v\). Du kan sjekke nærmere i Utforsk 3 at kalkulatorer som regner ut \(\sin v\) til en stump vinkel gjør nettopp dette.

Utforsk 3

Bruk CAS-vinduet nedenfor til å undersøke verdien til \(\sin v\) og \(\sin (180\degree - v)\) for følgende stumpe vinkler:

\[ v \in \{120\degree, 135\degree, 150\degree\} \]

CAS-vindu