Oppgaver: Sinussetningen

Oppgaver: Sinussetningen#

Oppgave 1

En trekant \(\triangle ABC\) er vist i figuren nedenfor.

a

Bestem \(a\).

Fasit

\[ a \approx 1.39 \]

Løsning

b

Bestem \(c\).

Fasit

\[ c = 2 \]

Løsning

Oppgave 2

I figuren nedenfor vises en trekant \(\triangle ABC\).

a

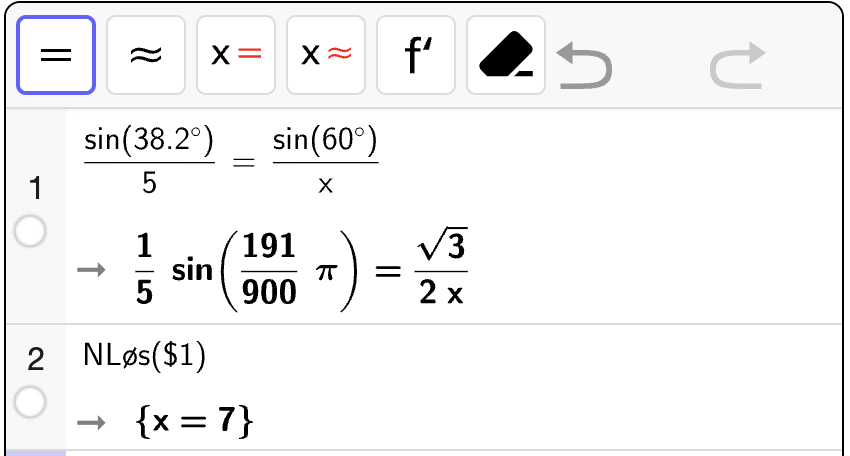
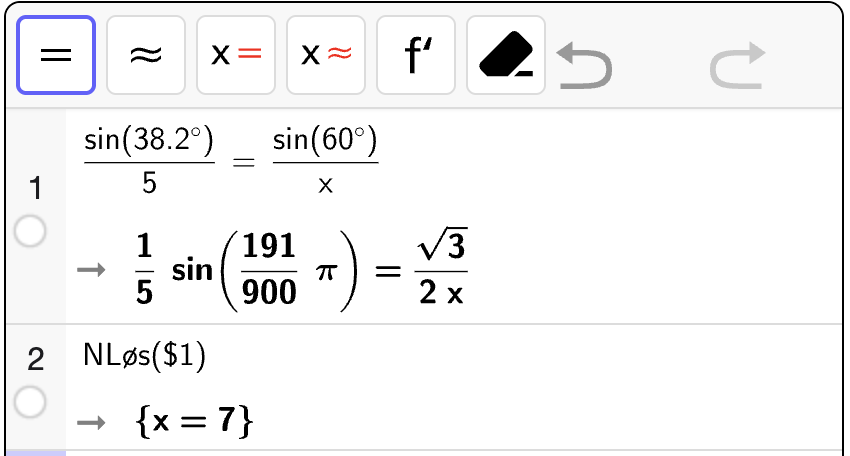
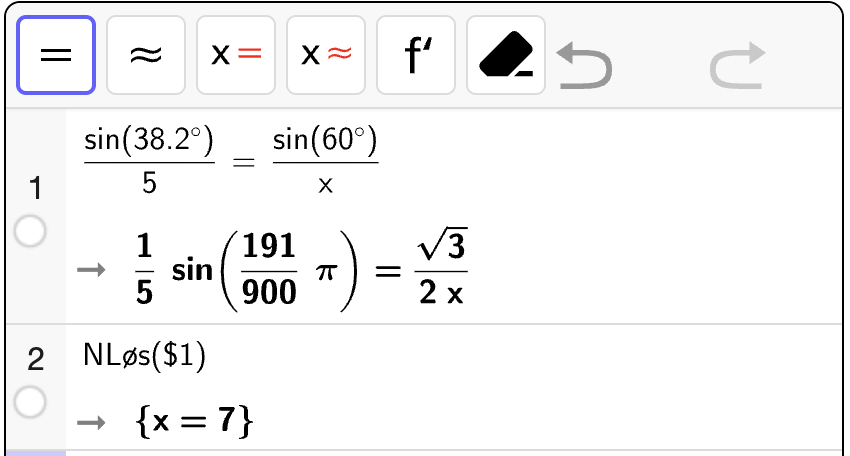
Bestem \(\angle B\).

Fasit

\[ \angle B \approx 88.39\degree \]

Løsning

Fra figuren kan vi se at \(\angle B < 90 \degree\). Dermed er

\[ \angle B \approx 88.39\degree. \]

b

Bestem \(BC\).

Fasit

\[ BC \approx 2.29 \]

Løsning

Altså er

\[ BC \approx 2.29 \]

c

Bestem arealet av \(\triangle ABC\).

Fasit

\[ T \approx 2.29 \]

Løsning

som betyr at arealet av \(\triangle ABC\) er

\[ T = \approx 2.29 \]

Oppgave 3

I \(\triangle ABC\) er \(\angle A = 45 \degree\), \(BC = 6\) og \(AC = 8\).

a

Bestem hvilke mulige vinkler \(\angle B\) kan ha.

Fasit

\[ \angle B \approx 70.53 \degree \or \angle B \approx 109.47 \degree \]

Løsning

Vinkelen \(\angle B\) kan enten være spiss eller stump. Vi bruker sinussetningen for å bestemme hvilke mulige verdier \(\angle B\) kan ha:

som betyr at

\[ \angle B \approx 70.53 \degree \or \angle B \approx 109.47 \degree. \]

b

Bestem hvilke to lengder \(AB\) kan ha.

Fasit

\[ AB \approx 3.66 \or AB \approx 7.66 \]

Løsning

Lengden til \(AB\) vil være avhengig av \(\angle B\). La oss først anta \(\angle B \approx 70.53 \degree\). Da kan vi bruke sinussetningen til å bestemme den ene lengden \(AB\) kan ha:

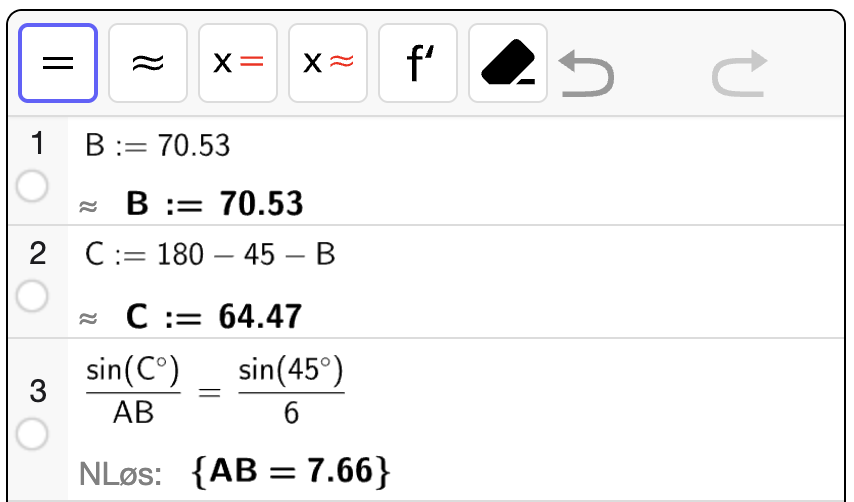
Altså kan vi ha

\[ \angle B \approx 70.53 \degree \and AB \approx 7.66. \]

Den andre mulige verdien for \(\angle B\) er \(\angle B \approx 109.47 \degree\). Da kan vi bruke sinussetningen til å bestemme den andre lengden \(AB\) kan ha:

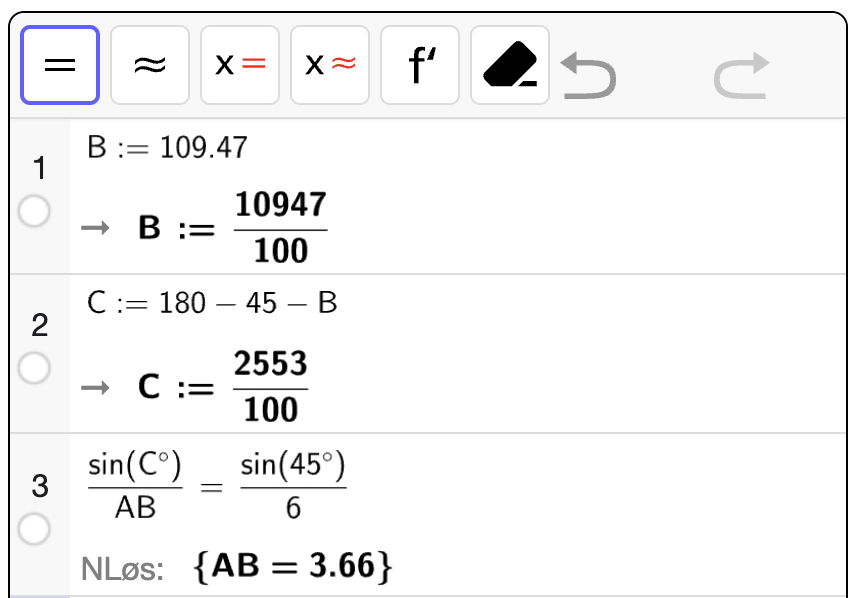
Altså kan vi ha

\[ \angle B \approx 109.47 \degree \and AB \approx 3.66. \]

Oppgave 4

I figuren nedenfor vises \(\square ABCD\).

a

Bestem \(\angle BDA\).

Fasit

\[ \angle BDA \approx 26.57\degree. \]

Løsning

Vi bruker sinussetningen til å bestemme \(\angle BDA\):

Altså er

\[ \angle BDA \approx 26.57\degree. \]

b

Bestem arealet \(T\) av \(\square ABCD\).

Fasit

\[ T_{ABCD} \approx 22.5 \]

Løsning

Vi bruker arealsetningen på de trekantene \(\triangle ABD\) og \(\triangle BCD\) for å bestemme arealet \(T\) av \(\square ABCD\):

Altså er

\[ T_{ABCD} \approx 22.5 \]

Oppgave 5

I figuren nedenfor vises \(\square ABCD\).

a

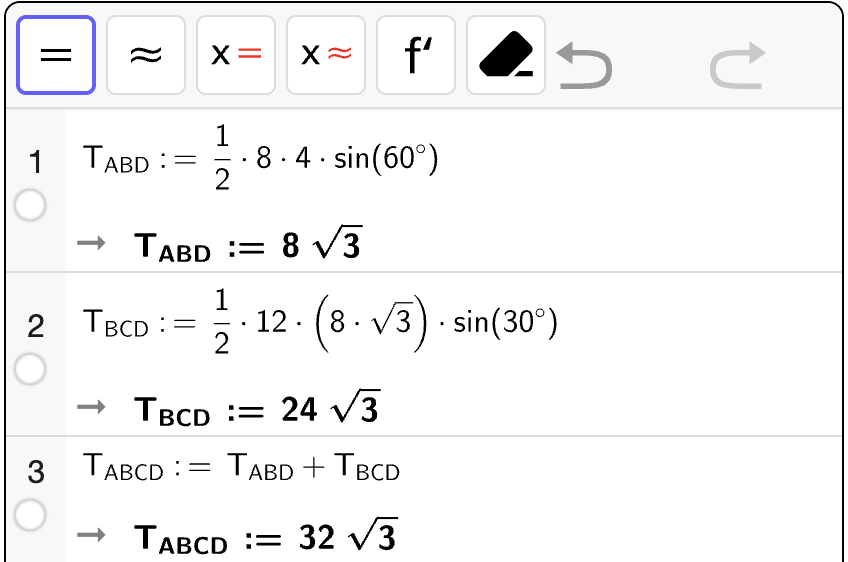
Bestem en eksakt verdi for \(CD\) uttrykt ved \(a\).

Fasit

\[ CD = \dfrac{\sqrt{3}}{2} a \]

Løsning

Vi bruker sinussetningen til å bestemme lengden \(CD\):

Altså er

\[ CD = \dfrac{\sqrt{3}}{2} a. \]

b

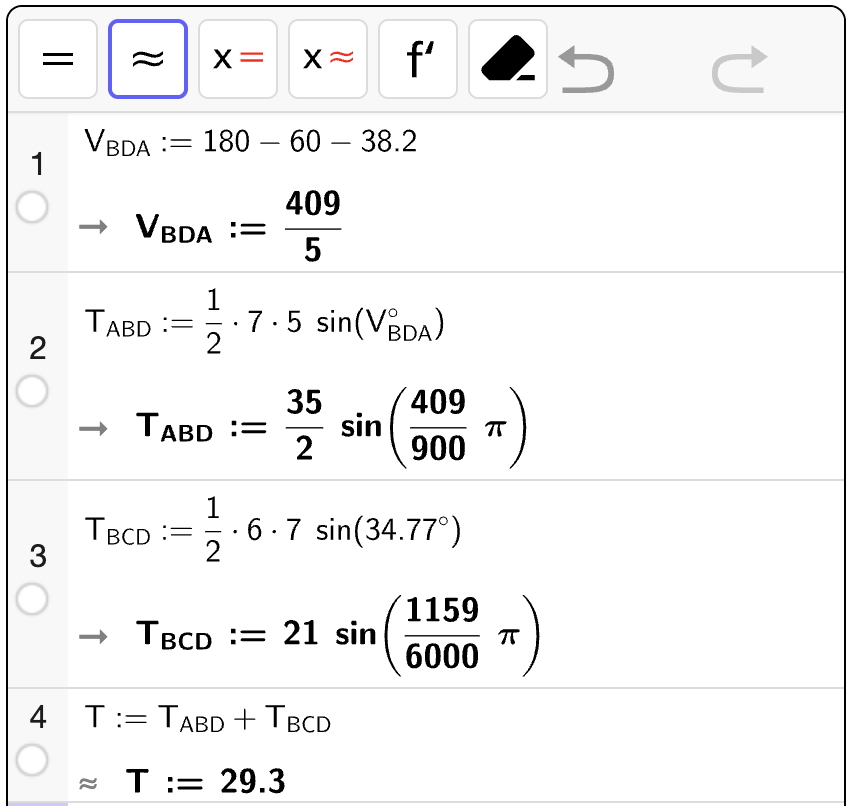
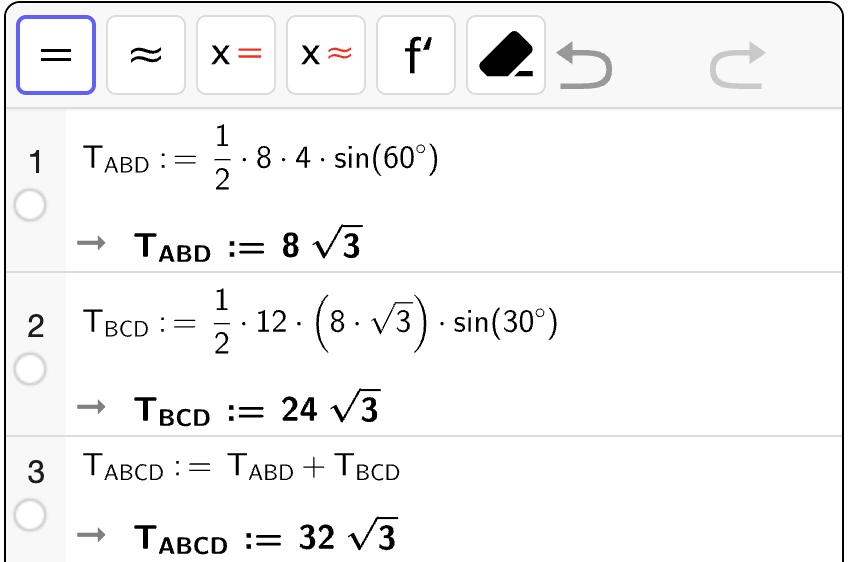
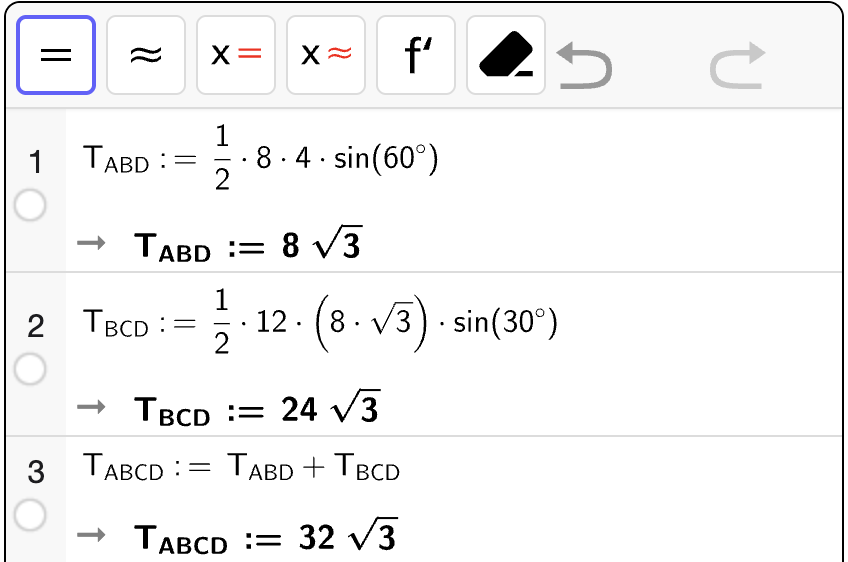
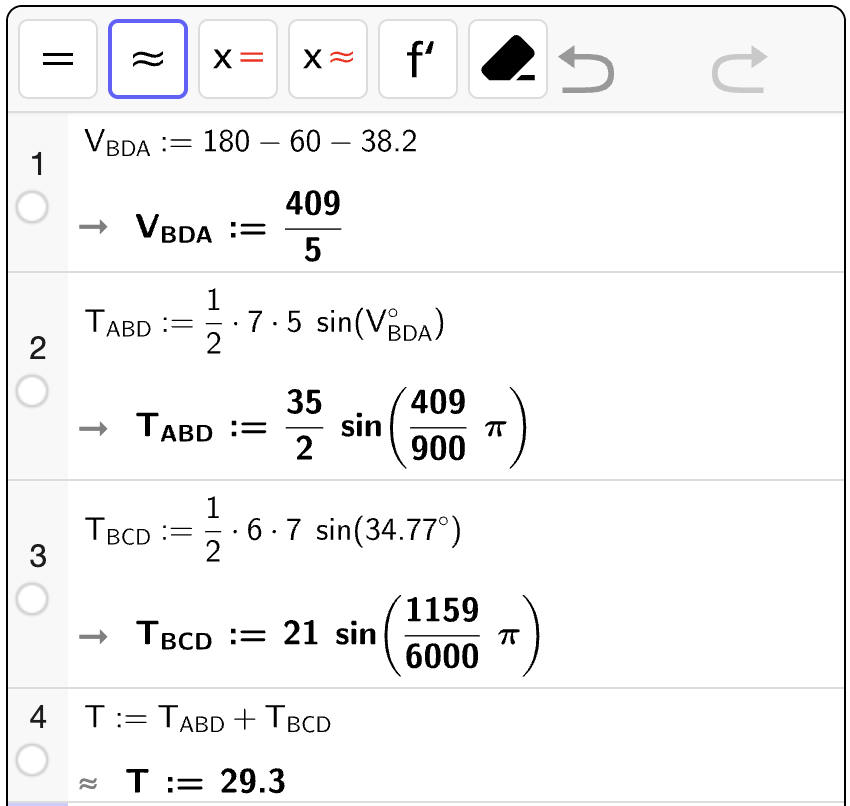
Bestem en eksakt verdi for arealet \(T\) av \(\square ABCD\) uttrykt ved \(a\).

Fasit

\[ T = \dfrac{1}{8}a^2 \left(2\sqrt{3} + 1\right) \]

Løsning

Vi bruker arealsetningen til å bestemme arealet av de to trekantene. Vi trenger én side til i \(\triangle ABD\), så vi finner \(AD\) ved hjelp av sinussetningen. Vi gjør utregningen med CAS:

Altså er

\[ T_{ABCD} = \dfrac{1}{8}a^2 \left(2\sqrt{3} + 1\right). \]

Oppgave 6

I figuren nedenfor vises \(\square ABCD\).

a

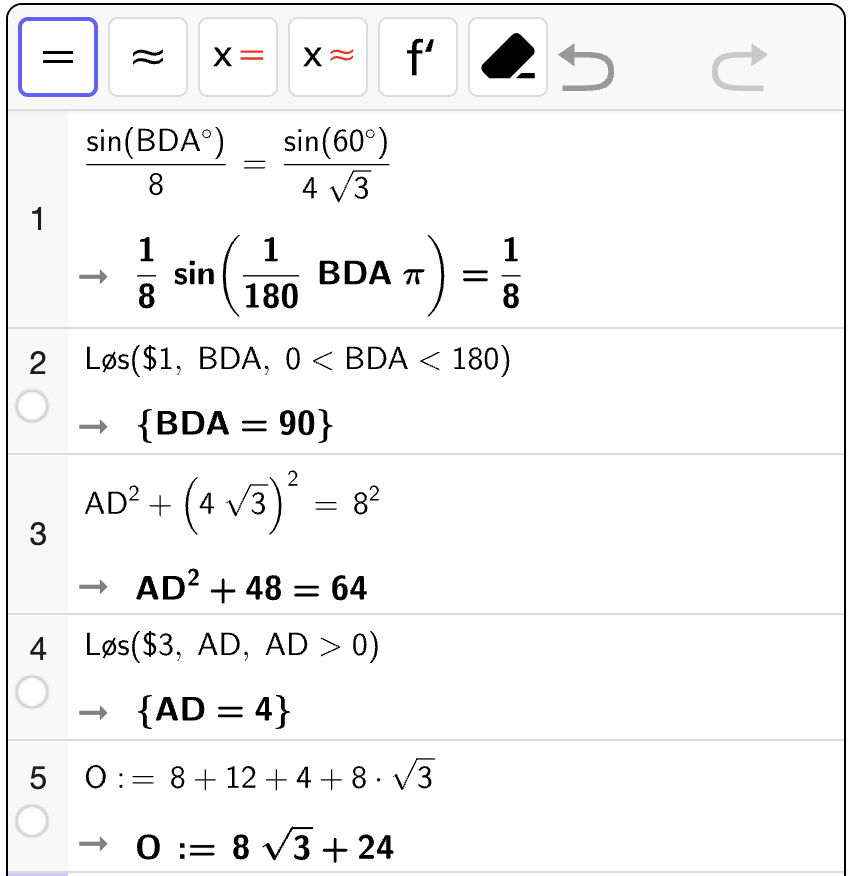
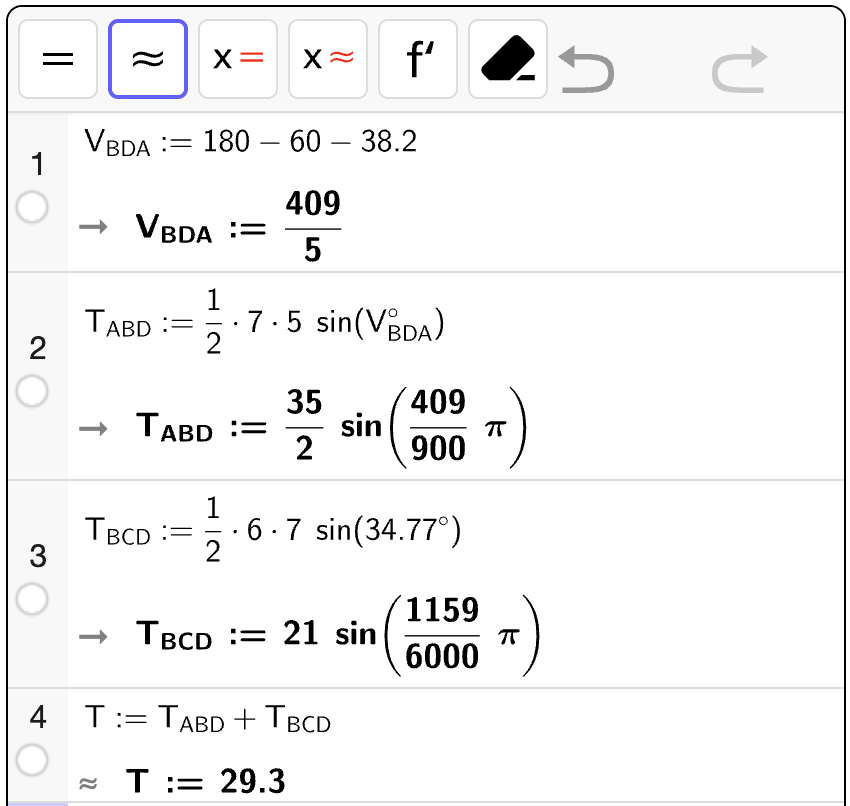
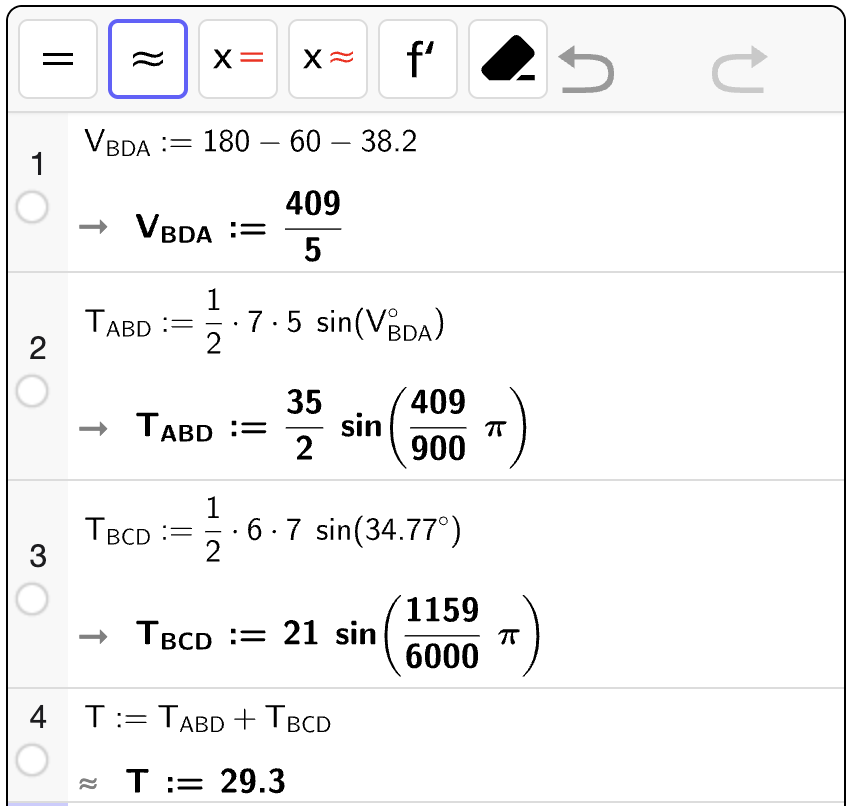
Bestem en eksakt verdi for omkretsen \(\mathcal{O}\) til \(\square ABCD\).

Fasit

\[ \mathcal{O} = 8\sqrt{3} + 24 \]

Løsning

Vi bruker først sinussetningen til å vinkelen \(\angle BDA\). Vi finner at \(\angle BDA = 90 \degree\) som betyr at vi kan bruke Pytagoras’ setning til å bestemme \(AD\). Deretter plusser vi sammen lengdene til alle sidene.

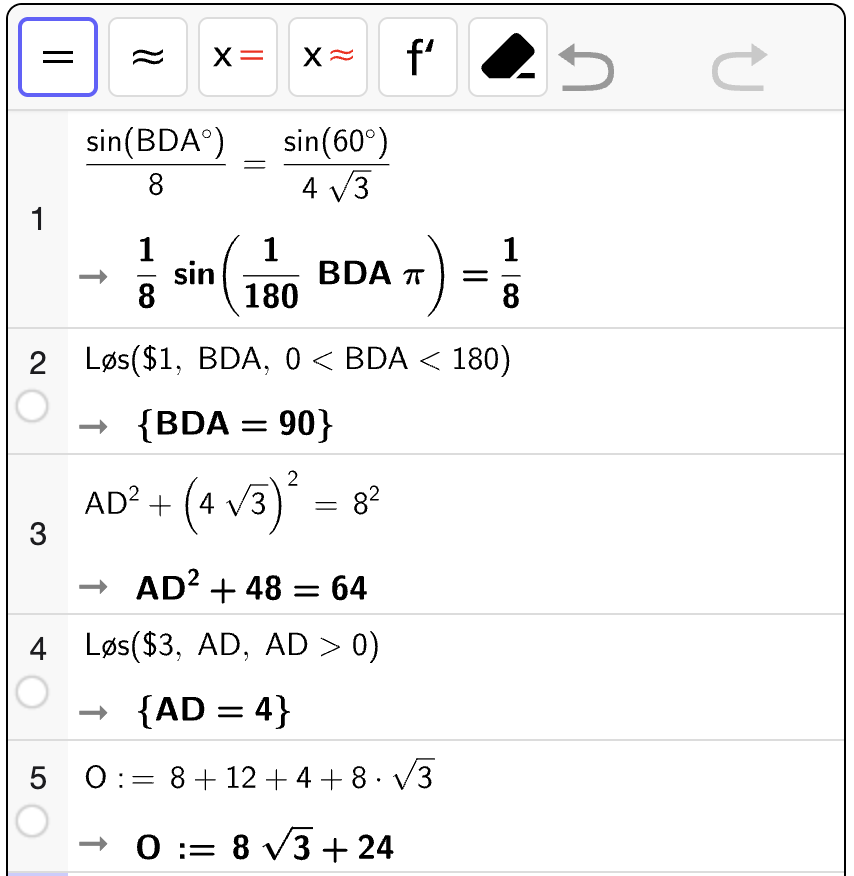
Omkretsen til \(\square ABCD\) er da

\[ \mathcal{O} = 8\sqrt{3} + 24 \]

b

Bestem en eksakt verdi for arealet \(T_{ABCD}\) til \(\square ABCD\).

Fasit

\[ T_{ABCD} = 32\sqrt{3} \]

Løsning

Vi bruker arealsetningen på hver av trekantene og legger sammen arealene:

Altså er arealet til \(\square ABCD\):

\[ T_{ABCD} = 32\sqrt{3} \]

Oppgave 7

I figuren nedenfor vises \(\square ABCD\).

a

Bestem lengden av diagonalen \(BD\).

Fasit

\[ BD = 7. \]

Løsning

Vi bruker sinussetningen til å bestemme lengden \(x = BD\):

Altså er

\[ BD = 7 \]

b

Bestem arealet \(T\) av \(\square ABCD\).

Fasit

\[ T \approx 29.3 \]

Løsning

Vi bruker arealsetningen på de to trekantene og legger sammen arealene:

Altså er arealet \(T\) av \(\square ABCD\):

\[ T \approx 29.3 \]