Oppgaver: Andregradslikninger

Oppgaver: Andregradslikninger#

Oppgave 1

a

Bruk Fig. 16.3 til å løse

\[ f(x) = 0 \]

../../../_images/a1.svg — Fig. 16.3 viser grafen til en andregradsfunksjon $f$.#

Fasit

\[ x = -3 \or x = 1 \]

b

Bruk Fig. 16.4 til å løse

\[ g(x) = 0 \]

../../../_images/b1.svg — Fig. 16.4 viser grafen til en andregradsfunksjon $g$.#

Fasit

\[ x = 1 \]

c

Bruk Fig. 16.5 til å løse

\[ h(x) = 0 \]

../../../_images/c1.svg — Fig. 16.5 viser grafen til en andregradsfunksjon $h$.#

Fasit

\[ x = -2 \or x = 2 \]

d

Bruk Fig. 16.6 til å løse

\[ p(x) = 0 \]

../../../_images/d1.svg — Fig. 16.6 viser grafen til en andregradsfunksjon $p$.#

Fasit

\[ x = -4 \or x = 3 \]

Oppgave 2

Hvordan løser jeg en likning grafisk med Geogebra?

Nedenfor vises en gif som viser hvordan man løser likningen

\[ x^2 - 4x + 3 = -2x + 6 \]

Vi trykker på GeoGebra mode_intersect icon (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktet.

../../../_images/grafisk_l%C3%B8sning.gif — Fig. 16.7 Løsningen er $x$-koordinatene til skjæringspunktene. Altså $x = -1 \or x = 3$.#

a

Løs likningen nedenfor grafisk.

\[ 2x^2 + 2x - 12 = 0 \]

Fasit

\[ x = -3 \or x = 2 \]

Løsning

Vi skriver inn likningene for venstre og høyre side av likningen og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktene. Se figuren nedenfor.

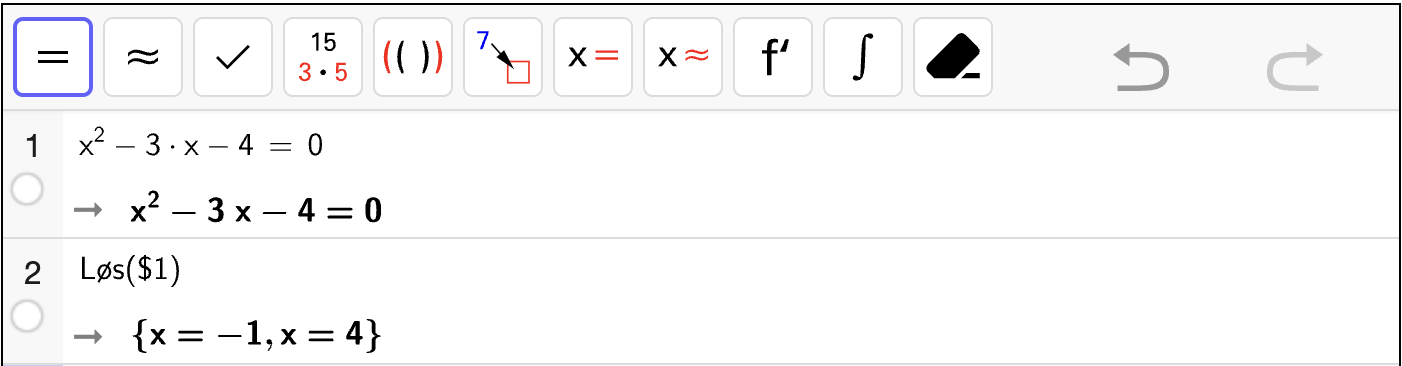
Vi ser at skjæringspunktene er $(-3, 0)$ og $(2, 0)$. Det er $x$-koordinatene som er løsningen av likningen, som betyr at løsningen er

\[ x = -3 \or x = 2 \]

b

Løs likningen nedenfor grafisk.

\[ 2x^2 - 4x = -2 \]

Fasit

\[ x = 1 \]

Løsning

Vi skriver inn likningene for venstre og høyre side av likningen og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktene. Se figuren nedenfor.

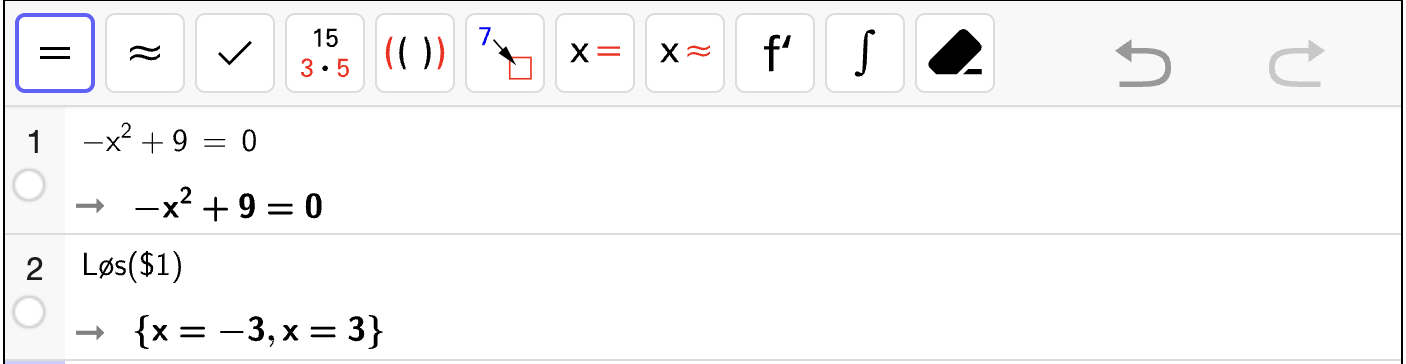
Vi ser at det er ett skjæringspunkt mellom grafene gitt ved $(1, -2)$. Det er $x$-koordinaten som er løsningen av likningen, som betyr at løsningen er

\[ x = 1 \]

c

Løs likningen nedenfor grafisk.

\[ x^2 + 2x - 2 = 4x + 6 \]

Fasit

\[ x = -2 \or x = 4 \]

Løsning

Vi skriver inn likningene for venstre og høyre side av likningen og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktene. Se figuren nedenfor.

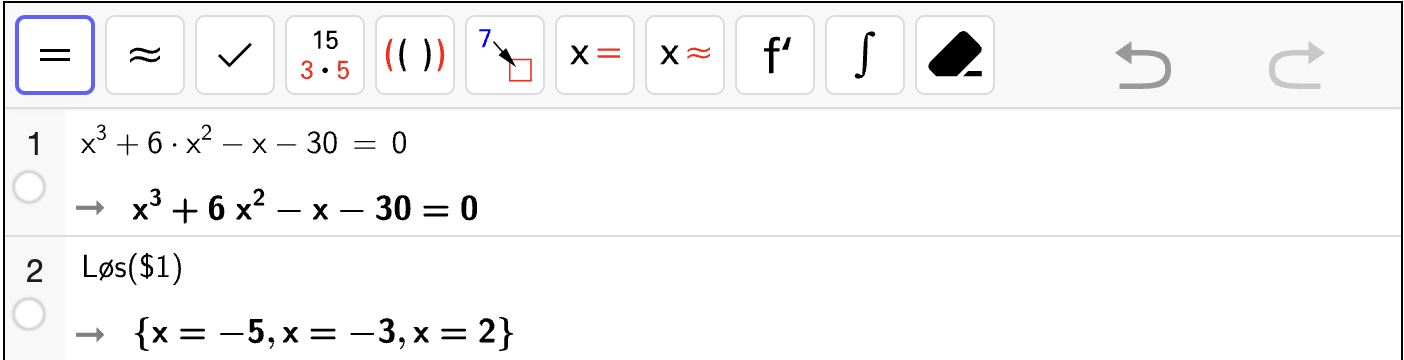
Vi ser at skjæringspunktene er $(-2, -2)$ og $(4, 22)$. Det er $x$-koordinatene som er løsningene av likningen, som betyr at løsningen er

\[ x = -2 \or x = 4 \]

d

Løs likningen nedenfor grafisk.

\[ 4x^2 - 12x + 6 = -2x^2 + 5x - 1 \]

Fasit

\[ x \approx 0.5 \or x \approx 2.33. \]

Løsning

Vi skriver inn likningene for venstre og høyre side av likningen og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktene. Se figuren nedenfor.

Vi ser at skjæringspunktene er $(0.5, 1)$ og $(2.33, -0.22)$. Det er $x$-koordinatene som er løsningene av likningen, som betyr at løsningen er

\[ x \approx 0.5 \or x \approx 2.33. \]

Her bruker vi $\approx$ fordi vi bare finner en tilnærmet verdi for $x$-koordinatene og ikke nødvendigvis den eksakte verdien.

Oppgave 3

a

Løs likningen

\[ x^2 - 4 = 0 \]

b

Løs likningen

\[ x^2 - 1 = 0 \]

c

Løs likningen

\[ x^2 - 16 = 0 \]

d

Løs likningen

\[ x^2 - 2 = 0 \]

Oppgave 4

a

Løs likningen

\[ x^2 - 5x = 0. \]

b

Løs likningen

\[ x^2 + 2x = 0. \]

c

Løs likningen

\[ x^2 - 10x = 0. \]

d

Løs likningen

\[ -x^2 + x = 0. \]

Oppgave 5

Løs likningene med $abc$-formelen.

a

\[ x^2 - 5x + 6 = 0 \]

Fasit

\[ x = 2 \or x = 3 \]

b

\[ x^2 - 3x - 4 = 0 \]

Fasit

\[ x = -1 \or x = 4 \]

c

\[ x^2 - x - 6 = 0 \]

Fasit

\[ x = -2 \or x = 3 \]

d

\[ x^2 - 4x - 5 = 0 \]

Fasit

\[ x = -1 \or x = 5 \]

Oppgave 6

Løs likningene ved hjelp av $abc$-formelen.

a

\[ 2x^2 - 5x + 2 = 0 \]

Fasit

\[ x = \dfrac{1}{2} \or x = 2 \]

b

\[ 3x^2 - 7x + 2 = 0 \]

Fasit

\[ x \in \left\{\dfrac{1}{3}, 2\right\} \]

c

\[ -x^2 + 9x + 12 = 0 \]

Fasit

\[ x = -1 \or x = 4 \]

d

\[ \dfrac{1}{2}x^2 - \dfrac{3}{4}x - \dfrac{1}{2} = 0 \]

Fasit

\[ x = -\dfrac{1}{2} \or x = 2 \]

Oppgave 7

Noen ganger jobber vi med andregradslikninger som vi må skrive om til formen $ax^2 + bx + c = 0$ før vi kan bruke $abc$-formelen.

Løs likningene med $abc$-formelen.

a

\[ x^2 + x + 1 = x + 5 \]

Fasit

\[ x = -2 \, \lor \, x = 2 \]

b

\[ x^2 + x - 3 = -2x + 1 \]

Fasit

\[ x = -4 \, \lor \, x = 1 \]

c

\[ -x^2 + x + 3 = 3x - 1 \]

Fasit

\[ x = -2 \, \lor \, x = 1 \]

d

\[ 2x^2 + 5x - 1 = -2x + 3 \]

Fasit

\[ x = \dfrac{1}{2} \or x = -4. \]

Oppgave 8

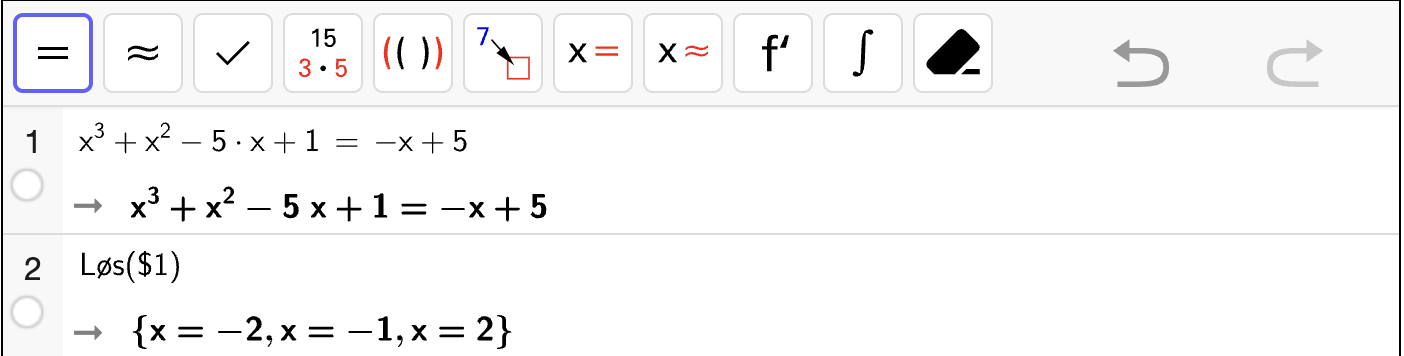
Løs likningene med CAS.

a

\[ x^2 + 2x + 1 = 0. \]

b

\[ x^2 - 3x + 2 = -x + 6 \]

c

\[ -x^2 + 3x + 1 = 2x - 7 \]

c

\[ -3x^2 + 4x + 6 = -3x + 10 \]

Oppgave 9

a

Nedenfor vises et program som løser en andregradslikning.

Bruk CAS til å bestemme verdiene programmet skriver ut og sjekk svaret ditt nedenfor.

b

Nedenfor vises et program som løser en andregradslikning.

Bruk CAS til å bestemme verdiene programmet skriver ut og sjekk svaret ditt nedenfor.

c

Nedenfor vises et program som løser en andregradslikning.

Bruk CAS til å bestemme verdiene programmet skriver ut og sjekk svaret ditt nedenfor.

d

Nedenfor vises et program som løser en andregradslikning.

Bruk CAS til å bestemme verdiene programmet skriver ut og sjekk svaret ditt nedenfor.

Oppgave 10

a

Fyll ut programmet og bruk det til å løse likningen

\[ x^2 + 2x - 8 = 0. \]

Fasit

for x in range(-10, 11):
    if x**2 + 2*x - 8 == 0:
        print(x)

b

Fyll ut programmet og bruk det til å løse likningen

\[ x^2 + 2x - 3 = 0. \]

Fasit

for x in range(-10, 11):
    if x**2 + 2*x - 3 == 0:
        print(x)

c

Fyll ut programmet og bruk det til å løse likningen

\[ x^2 - x - 3 = -3x + 12 \]

Fasit

for x in range(-10, 11):
    if x**2 - x - 3 == -3*x + 12:
        print(x)

d

Fyll ut programmet og bruk det til å løse likningen

\[ -x^2 + 6x + 7 = x^2 - 4x - 5 \]

Fasit

for x in range(-10, 11):
    if -x**2 + 6*x + 7 == x**2 - 4*x - 5:
        print(x)

Oppgave 11

a

Bestem $a$ og $b$ slik at likningen er en identitet.

\[ x^2 + 6x - 7 = (x - a)(x - b) \]

b

Bestem $a$, $b$ og $c$ slik at likningen er en identitet.

\[ -x^2 - 7x - 12 = a(x - b)(x - c) \]

c

Bestem $a$, $b$ og $c$ slik at likningen er en identitet.

\[ 2x^2 - 18 = a(x - b)(x - c) \]

d

Bestem $a$, $b$ og $c$ slik at likningen er en identitet.

\[ -3x^2 + 12x = a(x - b)(x - c) \]

Oppgave 12

a

Bestem diskriminanten $D$ for likningen

\[ x^2 + 10x + 25 = 0 \]

og avgjør hvor mange løsninger likningen har.

b

Bestem diskriminanten $D$ for likningen

\[ -x^2 + 3x + 8 = 0 \]

og avgjør hvor mange løsninger likningen har.

c

Bestem diskriminanten $D$ for likningen

\[ -x^2 + 3x + 8 = 0 \]

og avgjør hvor mange løsninger likningen har.

Oppgave 13

a

En andregradslikning er gitt ved

\[ x^2 + kx + 6 = 0. \]

Bestem $k$ slik at likningen har én løsning.

b

En andregradsfunksjon er gitt ved

\[ f(x) = kx^2 + kx - 2 \qder k \neq 0. \]

Bestem $k$ slik at grafen til $f$ skjærer $x$-aksen én gang.

c

En andregradsfunksjon $f$ er gitt ved

\[ f(x) = x^2 - 2kx + k, \qder k \in \real \]

Bestem $k$ slik at $f$ har nøyaktig ett nullpunkt.

Oppgave 14

Grafen til en andregradsfunksjon $f$ er vist nedenfor.

a

Bestem $f(x)$.

b

Bruk grafen til å løse likningen

\[ f(x) = 0 \]

c

Bruk $abc$-formelen til å løse likningen

\[ f(x) = 0 \]

d

Bruk CAS til å løse likningen

\[ f(x) = 14 \]

e

Skriv et program som løser likningen

\[ f(x) = 8 \]

Oppgave 15

Vi går ut ifra en helt generell andregradslikning

\[ ax^2 + bx + c = 0. \]

a

Forklar at vi kan skrive om likningen til

\[ a(x - x_0)^2 + y_0 = 0 \]

og bestem $x_0$ og $y_0$ uttrykt ved $a$, $b$ og $c$.

b

Forklar at løsningene av likningen er

\[ x = x_0 \pm \sqrt{-\frac{y_0}{a}}. \]

Bruk dette til å utlede $abc$-formelen.