Oppgaver: Ikke-lineære likningssystemer

Oppgaver: Ikke-lineære likningssystemer#

Oppgave 1

Bruk figuren nedenfor til å løse likningssystemet

\[\begin{align*} x^2 - 2x + y &= 4\\ \\ -x + y &= 2 \end{align*}\]
../../../_images/a2.svg

Fasit

\[ x = -1 \and y = 1 \or x = 2 \and y = 4. \]

Løsning

Vi ser fra figuren at grafene til likningene skjærer hverandre i punktene \((-1, 1)\) og \((2, 4)\). Løsningen av likningssystemet er derfor

\[ x = -1 \and y = 1 \or x = 2 \and y = 4. \]

Bruk figuren nedenfor til å løse likningssystemet

\[\begin{align*} x^2 + x - y &= 2\\ \\ -2x + y &= 4 \end{align*}\]
../../../_images/b2.svg

Fasit

\[ x = -2 \and y = 0 \or x = 3 \and y = 10. \]

Løsning

Grafene til likningene skjærer hverandre i punktene \((-2, 0)\) og \((3, 10)\). Løsniingen av likningssystemet er derfor

\[ x = -2 \and y = 0 \or x = 3 \and y = 10. \]

Bruk figuren nedenfor til å løse likningssystemet

\[\begin{align*} x^2 + 2x - y - 1 &= 0\\ \\ 3x - y &= -1 \end{align*}\]
../../../_images/c2.svg

Fasit

\[ x = -1 \and y = -2 \or x = 2 \and y = 7. \]

Løsning

Grafene skjærer hverandre i punktene \((-1, -2)\) og \((2, 7)\). Løsningen av likningssystemet er derfor

\[ x = -1 \and y = -2 \or x = 2 \and y = 7. \]

Bruk figuren nedenfor til å løse likningssystemet

\[\begin{align*} x^2 - 2x + y &= -1\\ \\ 2x + y &= 3 \end{align*}\]
../../../_images/d2.svg

Fasit

\[ x = 2 \and y = -1 \]

Løsning

Grafene skjærer hverandre i ett punkt: \((2, -1)\). Løsningen av likningssystemet er derfor

\[ x = 2 \and y = -1 \]

Oppgave 2

Bruk Geogebra til å løse likningssystemene grafisk.

Hvordan løser jeg likningssystemer grafisk med Geogebra?

Et likningssystem er gitt ved

\[\begin{align*} 2x - y &= 3 \\ x^2 - 2y - y &= 3 \end{align*}\]

Nedenfor ser du en gif som viser hvordan man løser likningen med grafvinduet i Geogebra. Vi trykker på GeoGebra mode_intersect icon (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktet.

../../../_images/grafisk_l%C3%B8sning1.gif

Skjæringspunktene mellom de to grafene er \((4, 5)\) og \((0, -3)\) som betyr at løsningen av likningssystemet er

\[ x = 4 \and y = 5 \or x = 0 \and y = -3 \]
\[\begin{align*} -x^2 + x + y &= 1 \\ \\ 3x + y &= 4 \end{align*}\]

Fasit

\[ x = -3 \and y = 13 \or x = 1 \and y = 1 \]

Løsning

Vi tegner grafene til likningene i Geogebra og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktet mellom dem. Se figuren nedenfor:

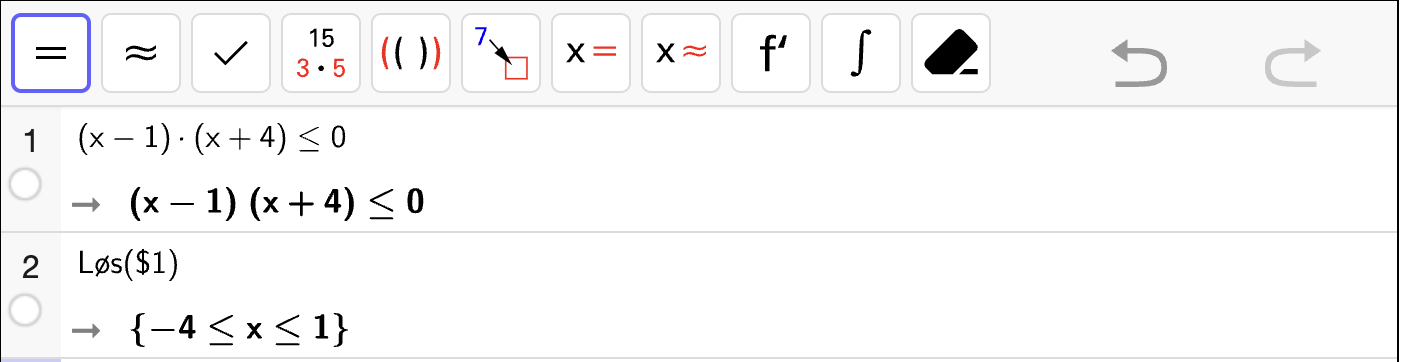
../../../_images/a1.png

Grafene skjærer hverandre i \((-3, 13)\) og \((1, 1)\). Da er løsningen av likningssystemet gitt ved

\[ x = -3 \and y = 13 \or x = 1 \and y = 1 \]
\[\begin{align*} x^2 - x - y &= 3 \\ \\ x - y &= -5 \end{align*}\]

Fasit

\[ x = -2 \and y = 3 \or x = 4 \and y = 9 \]

Løsning

Vi tegner grafene til likningene i Geogebra og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktet mellom dem. Se figuren nedenfor:

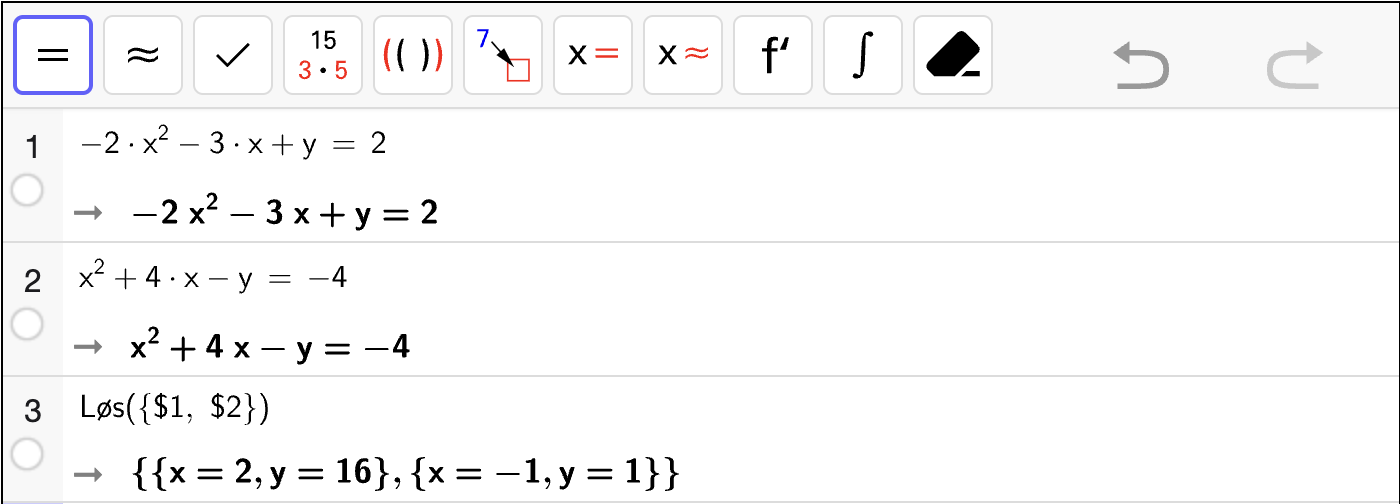
../../../_images/b2.png

Grafene skjærer hverandre i \((-2, 3)\) og \((4, 9)\). Da er løsningen av likningssystemet gitt ved

\[ x = -2 \and y = 3 \or x = 4 \and y = 9 \]
\[\begin{align*} x^2 + 2x - y &= 0 \\ \\ -2x + y &= 1 \end{align*}\]

Fasit

\[ x = -1 \and y = -1 \or x = 1 \and y = 3 \]

Løsning

Vi tegner grafene til likningene i Geogebra og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktet mellom dem. Se figuren nedenfor:

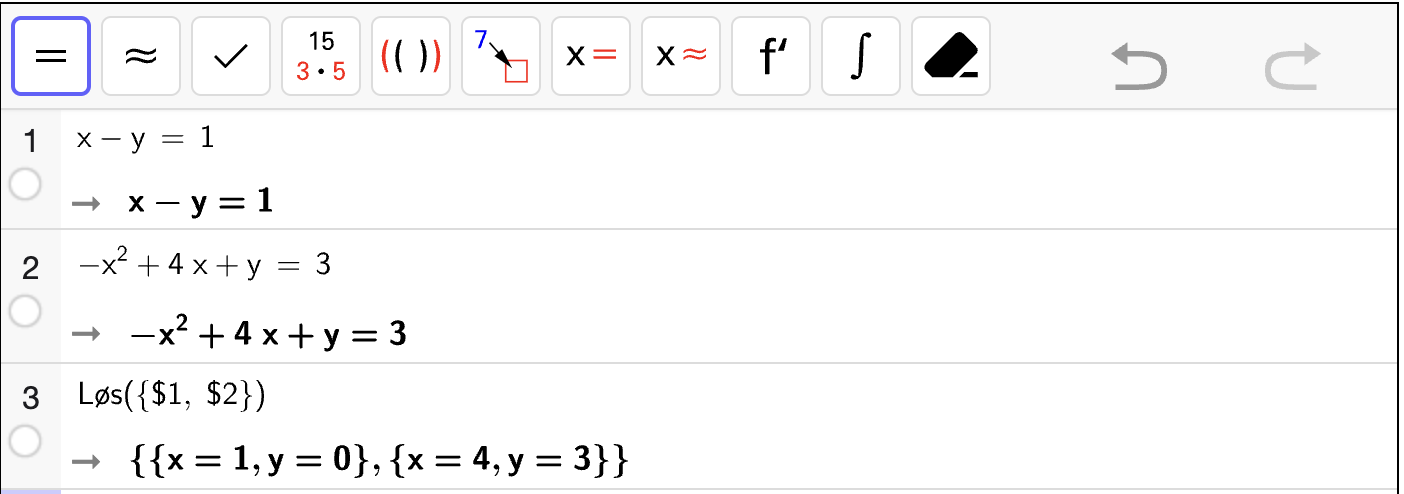
../../../_images/c2.png

Grafene skjærer hverandre i \((-1, -1)\) og \((1, 3)\). Da er løsningen av likningssystemet gitt ved

\[ x = -1 \and y = -1 \or x = 1 \and y = 3 \]
\[\begin{align*} -x^2 + x - y &= -1 \\ \\ 2x + y &= 1 \end{align*}\]

Fasit

\[ x = 0 \and y = 1 \or x = 4 \and y = -7 \]

Løsning

Vi tegner grafene til likningene i Geogebra og bruker “skjæring mellom to objekt” GeoGebra mode_intersect icon for å finne skjæringspunktet mellom dem. Se figuren nedenfor:

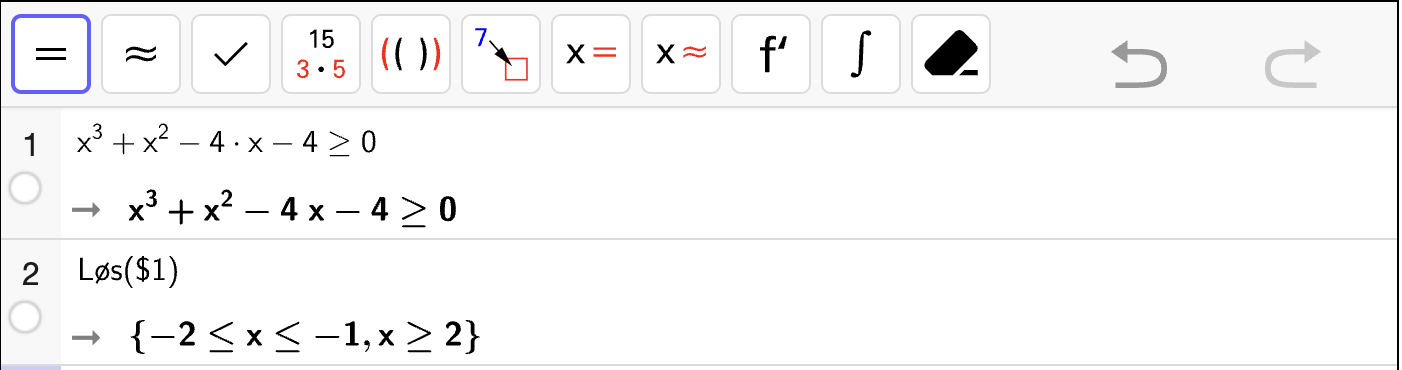
../../../_images/d1.png

Grafene skjærer hverandre i \((0, 1)\) og \((4, -7)\). Da er løsningen av likningssystemet gitt ved

\[ x = 0 \and y = 1 \or x = 4 \and y = -7 \]

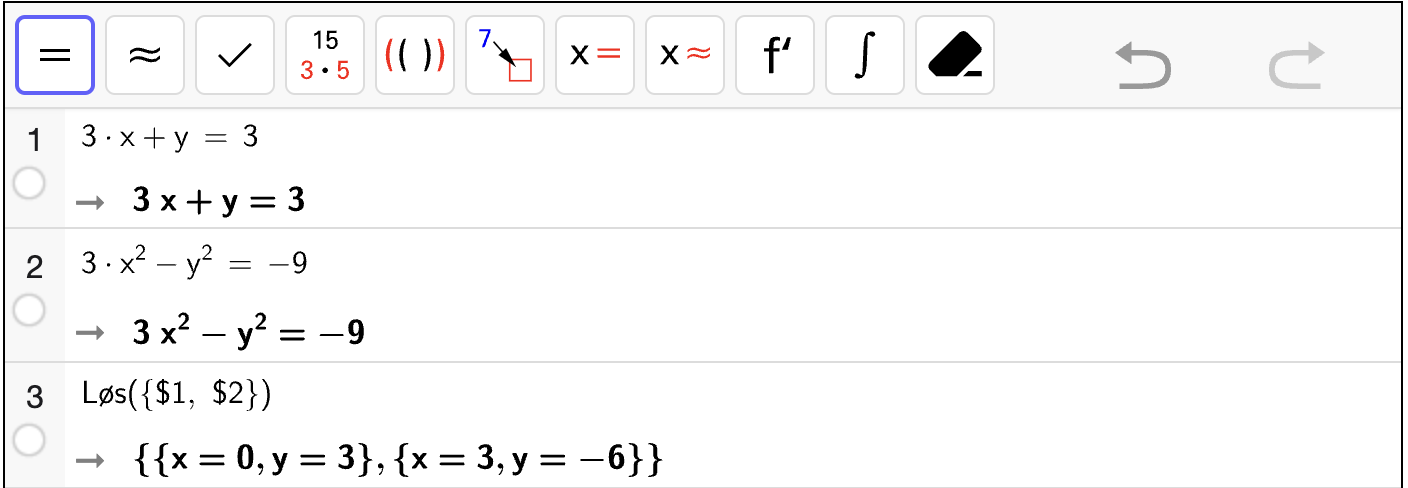
Oppgave 3

Løs likningssystemene algebraisk.

\[\begin{align*} x^2 - 2x + y &= 4\\ \\ -x + y &= 2 \end{align*}\]

Fasit

\[ x = -1 \and y = 1 \or x = 2 \and y = 4. \]

Løsning

Vi løser likning 2 for \(y\):

\[ -x + y = 2 \liff y = x + 2 \]

Deretter setter vi inn uttrykket for \(y\) i likning 1:

\[ x^2 - 2x + (x + 2) = 4 \]
\[ x^2 - x - 2 = 0 \]

Nå kan vi bruke \(abc\)-formelen for å finne verdiene for \(x\):

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{1 \pm \sqrt{1 + 8}}{2} = \frac{1 \pm 3}{2} \]

som gir løsningene

\[ x = -1 \or x = 2. \]

Hver verdi for \(x\) gir oss en verdi for \(y\). Vi bruker at \(y = x + 2\) og setter inn verdiene for \(x\). Når \(x = -1\), så får vi

\[ y = -1 + 2 = 1 \]

Når \(x = 2\), så får vi

\[ y = 2 + 2 = 4. \]

Dermed er løsningen av likningssystemet

\[ x = -1 \and y = 1 \or x = 2 \and y = 4. \]
\[\begin{align*} x^2 + x - y &= 2\\ \\ -2x + y &= 4 \end{align*}\]

Fasit

\[ x = -2 \and y = 0 \or x = 3 \and y = 10. \]

Løsning

Vi løser likning 2 for \(y\):

\[ -2x + y = 4 \liff y = 2x + 4 \]

Deretter setter vi inn uttrykket for \(y\) i likning 1:

\[ x^2 + x - (2x + 4) = 2 \]

Så forenkler vi likningen så mye som mulig:

\[ x^2 - x - 6 = 0 \]

Nå kan vi bruke \(abc\)-formelen for å finne verdiene for \(x\):

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{1 \pm \sqrt{1 + 24}}{2} = \frac{1 \pm 5}{2} \]

som gir løsningene

\[ x = -2 \or x = 3. \]

Hver verdi for \(x\) gir oss en verdi for \(y\). Vi bruker at \(y = 2x + 4\) og setter inn verdiene for \(x\). Når \(x = -2\), så får vi

\[ y = 2 \cdot (-2) + 4 = -4 + 4 = 0 \]

Når \(x = 3\), så får vi

\[ y = 2 \cdot 3 + 4 = 6 + 4 = 10. \]

Dermed er løsningen av likningssystemet

\[ x = -2 \and y = 0 \or x = 3 \and y = 10. \]
\[\begin{align*} 3x - y &= -1 \\ \\ x^2 + 2x - y &= 1\\ \end{align*}\]

Fasit

\[ x = -1 \and y = -2 \or x = 2 \and y = 7. \]

Løsning

Vi løser likning 1 for \(y\):

\[ 3x - y = -1 \liff y = 3x + 1 \]

Deretter setter vi inn uttrykket for \(y\) i likning 2:

\[ x^2 + 2x - (3x + 1) = 1 \]

Så forenkler vi likningen så mye som mulig:

\[ x^2 - x - 2 = 0 \]

Nå kan vi bruke \(abc\)-formelen for å finne verdiene for \(x\):

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{1 \pm \sqrt{1 + 8}}{2} = \frac{1 \pm 3}{2} \]

som gir løsningene

\[ x = -1 \or x = 2. \]

Hver verdi for \(x\) gir oss en verdi for \(y\). Vi bruker at \(y = 3x + 1\) og setter inn verdiene for \(x\). Når \(x = -1\), så får vi

\[ y = 3 \cdot (-1) + 1 = -3 + 1 = -2 \]

Når \(x = 2\), så får vi

\[ y = 3 \cdot 2 + 1 = 6 + 1 = 7. \]

Dermed er løsningen av likningssystemet

\[ x = -1 \and y = -2 \or x = 2 \and y = 7. \]
\[\begin{align*} x^2 - 2x + y &= -1\\ \\ 2x + y &= 3 \end{align*}\]

Fasit

\[ x = 2 \and y = -1. \]

Løsning

Vi løser likning 2 for \(y\):

\[ 2x + y = 3 \liff y = -2x + 3 \]

Deretter setter vi inn uttrykket for \(y\) i likning 1:

\[ x^2 - 2x + (-2x + 3) = -1 \]

Så forenkler vi likningen så mye som mulig:

\[ x^2 - 4x + 4 = 0 \]

Vi kan faktorisere likningen med 2.kvadratsetning:

\[ (x - 2)^2 = 0 \]

Det betyr at løsningen for \(x\) er

\[ x = 2. \]

Den tilhørende \(y\)-verdien finner vi ved å bruke at \(y = -2x + 3\):

\[ y = -2 \cdot 2 + 3 = -4 + 3 = -1. \]

Dermed er løsningen av likningssystemet

\[ x = 2 \and y = -1. \]

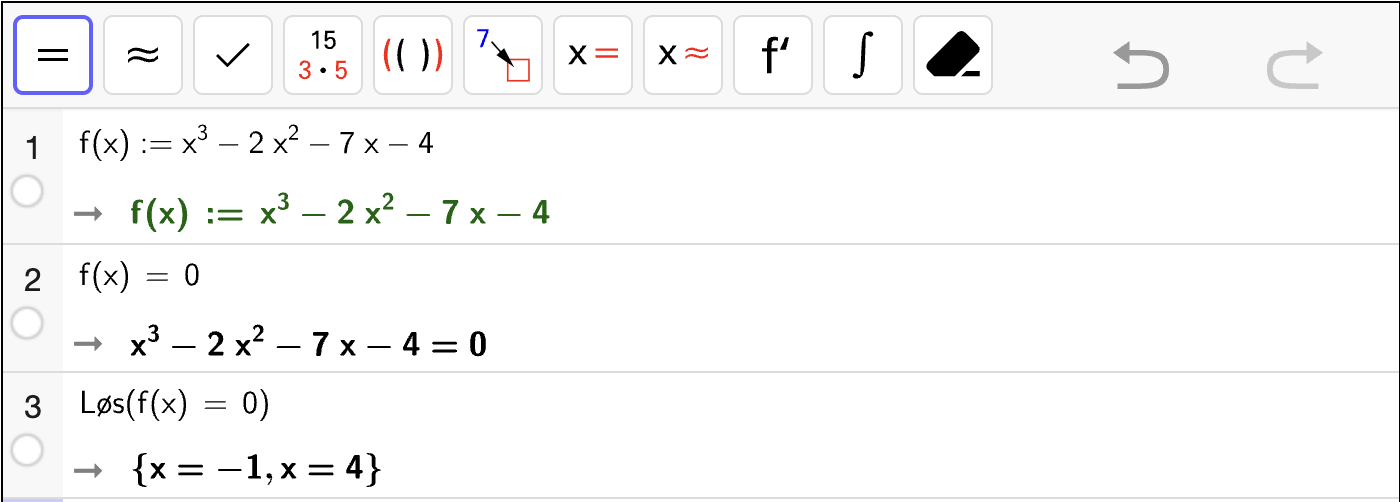
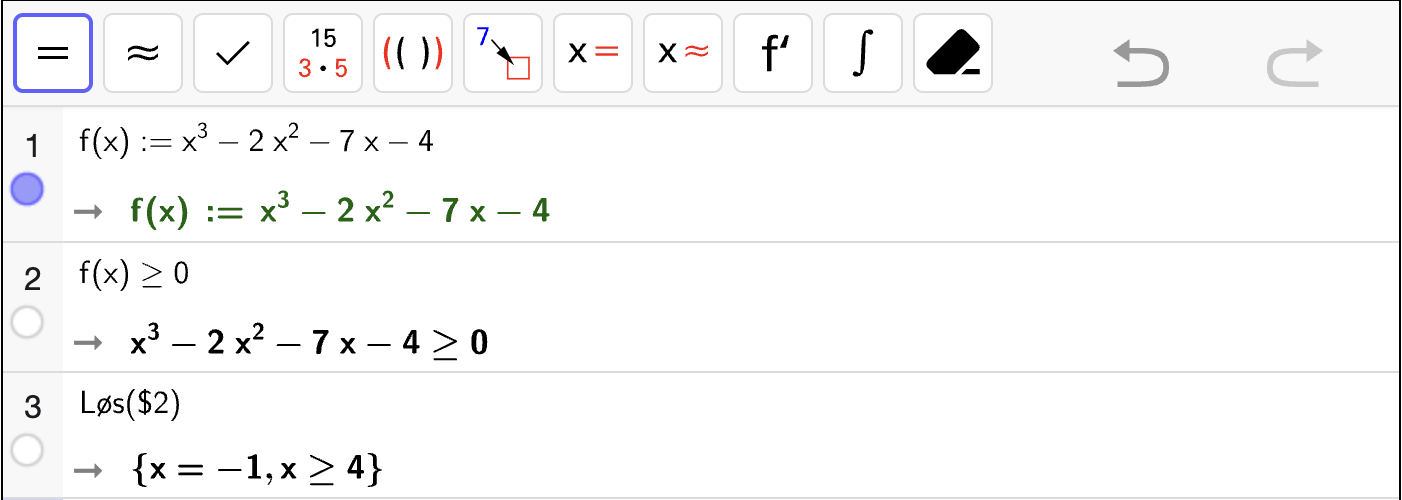
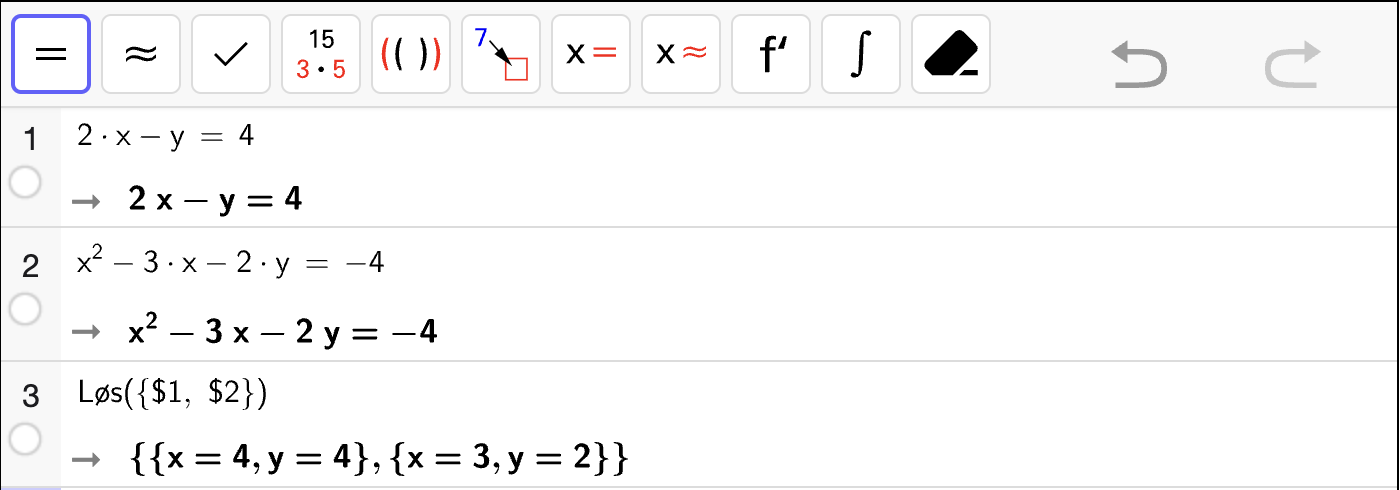
Oppgave 4

Bruk CAS til å løse likningssystemene.

\[\begin{align*} -x^2 + 3x + 4y &= 0 \\ \\ -x + 2y &= -2 \end{align*}\]

Fasit

\[ x = 4 \and y = 1 \or x = 1 \and y = -\dfrac{1}{2} \]

Løsning

../../../_images/a2.png

Fra utskriften ser vi at løsningen av likningssystemet er

\[ x = 4 \and y = 1 \or x = 1 \and y = -\dfrac{1}{2} \]
\[\begin{align*} 2x^2 - 3x - y &= 2 \\ \\ 2x - y &= -5 \end{align*}\]

Fasit

\[ x = -1 \and y = 3 \or x = \dfrac{7}{2} \and y = 12. \]

Løsning

../../../_images/b3.png

Fra utskriften ser vi at løsningen av likningssystemet er

\[ x = -1 \and y = 3 \or x = \dfrac{7}{2} \and y = 12. \]
\[\begin{align*} -x^2 + y &= 2 \\ \\ x + 4y &= 8 \end{align*}\]

Fasit

\[ x = 0 \and y = 2 \or x = -\dfrac{1}{4} \and y = \dfrac{33}{16} \]

Løsning

../../../_images/c3.png

Fra utskriften ser vi at løsningen av likningssystemet er

\[ x = 0 \and y = 2 \or x = -\dfrac{1}{4} \and y = \dfrac{33}{16} \]
\[\begin{align*} 2x - y &= 3 \\ \\ x^2 - 3 &= y + 2x \end{align*}\]

Fasit

\[ x = 0 \and y = -3 \or x = 4 \and y = 5. \]

Løsning

../../../_images/d2.png

Fra utskriften ser vi at løsningen av likningssystemet er

\[ x = 0 \and y = -3 \or x = 4 \and y = 5. \]

Oppgave 5

Avgjør hvilken av figurene nedenfor du kan bruke til å løse likningssystemet

\[\begin{align*} x^2 - 2x + y &= -2 \\ x - y &= 0 \end{align*}\]

Løs likningssystemet ved hjelp av riktig figur.

../../../_images/merged_figure5.svg

Fasit

Figur C.

Avgjør hvilken av figurene nedenfor du kan bruke til å løse likningssystemet

\[\begin{align*} x^2 - 6x - y &= -5\\ x - y &= 5 \end{align*}\]

Løs likningssystemet ved hjelp av riktig figur.

../../../_images/merged_figure6.svg

Fasit

Figur A.

Avgjør hvilken av figurene nedenfor du kan bruke til å løse likningssystemet

\[\begin{align*} x^2 + 2x + y &= 1 \\ x^2 - 4x - y &= 3 \end{align*}\]

Løs likningssystemet ved hjelp av riktig figur.

../../../_images/merged_figure7.svg

Fasit

Figur D.

Oppgave 6

Lag et likningssystem du kan bruke figuren nedenfor til å løse

../../../_images/a3.svg

Lag et likningssystem du kan bruke figuren nedenfor til å løse

../../../_images/b3.svg

Lag et likningssystem du kan bruke figuren nedenfor til å løse

../../../_images/c3.svg

Oppgave 7

Bruk CAS til å forutsi hva som skrives ut av programmene nedenfor.

Bruk CAS til å avgjøre hva som blir skrevet ut av programmet nedenfor.

Skriv inn svaret ditt og sjekk.

Bruk CAS til å avgjøre hva som blir skrevet ut av programmet nedenfor.

Skriv inn svaret ditt og sjekk.

Bruk CAS til å avgjøre hva som blir skrevet ut av programmet nedenfor.

Skriv inn svaret ditt og sjekk.

Bruk CAS til å avgjøre hva som blir skrevet ut av programmet nedenfor.

Skriv inn svaret ditt og sjekk.

Oppgave 8

Anna har skrevet et program for å løse et likningssystem. Programmet er vist nedenfor.

1for x in range(-100, 101):
2    for y in range(-100, 101):
3        if x**2 + y**2 == 25 and x + y == 5:
4            print((x, y))

Løs likningssystemet grafisk.

Løs likningssystemet med CAS.

Løs likningssystemet algebraisk.

Oppgave 9

Et likningssystem er gitt ved

\[\begin{align*} -x^2 + y &= k \\ 4x + y &= 5 \end{align*}\]

Bestem \(k\) slik at likningssystemet har nøyaktig én løsning.

Fasit

\[ k = 9 \]

For hvilke verdier av \(k\) har likningssystemet to løsninger?

Fasit

\[ k > 9 \]

Oppgave 10

Et likningssystem er gitt ved

\[\begin{align*} x^2 + kx + y &= 0 \\ x + y &= 2 \end{align*}\]

Bestem \(k\) slik at likningssystemet har nøyaktig én løsning.

Fasit

\[ k = -1 \or k = 3. \]

For hvilke verdier av \(k\) vil likningsystemet ikke ha noen løsning?

Fasit

\[ k \in \langle \gets, -1 \rangle \cup \langle 3, \gets \rangle \]

Oppgave 11

Grafen til en andregradsfunksjon kalles for en parabel. Men en parabel må ikke være en funksjon. For at grafen skal være en funksjon, så kan det bare finnes én \(y\)-verdi for hver \(x\)-verdi. Hvis parabelen derimot ligger langs \(x\)-aksen, så har den flere \(y\)-verdier for hver \(x\)-verdi. Da er ikke grafen en funksjon, men en kurve.

I figuren nedenfor vises en slik parabel.

../../../_images/a4.svg

Bestem likningen til parabelen på standardform:

\[ x = ay^2 + by + c \]

Bestem likningen til parabelen på ekstremalpunktssform:

\[ x = a(y - y_0)^2 + x_0 \]

Bestem likningen til parabelen på nullpunktsform:

\[ x = a(y - y_1)(y - y_2) \]