21. Polynomdivisjon

Læringsmål

• Kunne beskrive og utføre polynomdivisjon.

• Kunne forklare hva som er kvotient og rest i en polynomdivisjon, og forklare hva resten forteller oss om dividenden.

• Kunne bruke polynomdivisjon til å regne ut funksjonsverdier.

Polynomdivisjon er en metode for å dele et polynom med et annet polynom og skrive det på en enklere måte. Før vi ser på dette, skal vi motivere hvorfor vi trenger polynomdivisjon i det hele tatt. Vi har sett at når en tredjegradsfunksjon ett nullpunkt, så kan vi skrive \(f(x)\) som et produkt av et førstegradspolynom og et andregradspolynom på formen:

\[ f(x) = (x - x_1)(ax^2 + bx + c). \]

Men dette vil også fungere om en tredjegradsfunksjon har to eller tre nullpunker også. Det betyr bare at andregradspolynomet har ett eller to nullpunkter! Dette kan vi oppsummere med setningen nedenfor.

Algebraens fundamentalsetning for tredjegradspolynomer

Et tredjegradspolynom \(f(x)\) kan alltid skrives som et produkt av et førstegradspolynom og et andregradspolynom

\[ f(x) = (x - x_1)(ax^2 + bx + c). \]

Her er \(x = x_1\) et nullpunkt for \(f\). Andregradspolynomet kan ha ingen, ett eller to nullpunkter.

Setningen over forteller oss at hvis vi klarer å finne en faktor \((x - x_1)\) som deler \(f(x)\), så får vi et andregradspolynom. Siden vi vet hvordan vi bestemmer alle egenskapene til andregradspolynomer allerede, betyr det at vi har en mulig metode for å finne ut alt om tredjegradspolynomer også.

Vårt neste steg er derfor å se på en algoritme for å dele et polynom med en faktor \((x - x_1)\). Vi starter med å se på et eksempel med et andregradspolynom.

Polynomdivisjon uten rest

Eksempel 1

Regn ut:

\[ (3x^2 + 3x - 6) : (x + 2). \]

Løsning

Først tenker vi oss hva vi må gange \((x + 2)\) med slik at vi minst får et ledd med \(3x^2\). Dette vil være \(3x\). Ganger vi \(3x\) med \((x + 2)\), så får vi \(3x^2 + 6x\). Vi trekker fra dette fra \(3x^2 + 3x - 6\). Vi skriver dette slik:

Nå sitter vi igjen med en rest \((-3x + 6)\). Dette er hvor mye vi “bommet” på det riktig svaret ved å velge \(3x\). Vi kan nå gjenta samme prosess med resten. Hva må vi gange med \((x + 2)\) slik at minst et av leddene blir \(-3x\). Det vil være \(-3\). Ganger vi \(-3\) med \((x + 2)\) får vi \(-3x + 6\). Vi trekker dette fra resten og får:

Nå er resten vår \(0\) og vi er ferdig med divisjonen. Det betyr at

\[ (3x^2 + 3x - 6) : (x + 2) = 3x - 3 \liff \dfrac{3x^2 + 3x - 6}{x + 2} = 3x - 3 \]

---

Vi ser på et eksempel til med et tredjegradspolynom i telleren.

Eksempel 2

Utfør polynomdivisjonen

\[ (x^3 - 3x^2 - 6x + 8) : (x + 2). \]

Løsning

Først er vi etter hva vi må gange \((x + 2)\) med slik at vi får et polynom som har et ledd \(x^3\). Det får vi hvis vi ganger med \(x^2\). Ganger vi \(x^2\) med \((x + 2)\), får vi \(x^3 + 2x^2\). Vi trekker fra dette fra telleren:

Nå sitter vi igjen med en rest \((-5x^2 - 6x)\). Nå ser vi etter hva vi må gange \((x + 2)\) med slik at ett av leddene blir \(-5x^2\). Dette vil være \(-5x\). Ganger vi \(-5x\) med \((x + 2)\), får vi \(-5x^2 - 10x\). Vi trekker fra dette fra resten:

Nå sitter vi igjen med en rest \((4x + 8)\). Nå ser vi etter hva vi må gange \((x + 2)\) med slik at ett av leddene blir \(4x\). Dette vil være \(4\). Ganger vi \(4\) med \((x + 2)\), får vi \(4x + 8\). Vi trekker fra dette fra resten:

Nå har vi \(0\) i rest og er ferdig med divisjonen. Da har vi funnet at

\[ (x^3 - 3x^2 - 6x + 8) : (x + 2) = x^2 - 5x + 4 \]

som vi også kan skrive som

\[ \dfrac{x^3 - 3x^2 - 6x + 8}{x + 2} = x^2 - 5x + 4 \]

Ganger vi med \((x + 2)\) på hver side, så finner vi at vi kan faktorisere tredjegradspolynomet som

\[ x^3 - 3x^2 - 6x + 8 = (x + 2)(x^2 - 5x + 4) \]

---

Vi kan også utføre polynomdivisjon når divisoren er et andregradspolynom.

Eksempel 3

Utfør polynomdivisjonen

\[ (x^3 - 8x^2 + 21x - 18) : (x^2 - 6x + 9). \]

Løsning

Utregningen forteller oss at

\[ \dfrac{x^3 - 8x^2 + 21x - 18}{x^2 - 6x + 9} = x - 2 \]

som betyr at vi kan skrive at

\[ x^3 - 8x^2 + 21x - 18 = (x - 2)(x^2 - 6x + 9). \]

Polynomdivisjon med rest

Som vi så i begynnelsen av dette delkapittelet, så er \(f(x)\) bare delelig med en faktor \((x - x_1)\) hvis faktoren er i \(f(x)\). Det er da naturlig å lure på hva som skjer dersom \((x - x_1)\) ikke er en faktor i \(f(x)\). Da får vi en rest i polynomdivisjonen. La oss se på et eksempel:

Eksempel 4

Regn ut

\[ (x^3 - 5x^2 + 8x - 4) : (x - 3). \]

Løsning

Vi utfører polynomdivisjon:

Ved å følge stegene som før, får vi nå \(2\) i rest. Dette betyr at vi må legge på et ledd \(\dfrac{2}{x - 3}\) siden vi ikke kan dele noe mer. Dette forteller oss at

\[ \dfrac{x^3 - 5x^2 + 8x - 4}{x - 3} = x^2 - 2x + 2 + \dfrac{2}{x - 3}. \]

Siden vi ikke har \(0\) i rest, vil ikke \((x - 3)\) være en faktor i \(x^3 - 5x^2 + 8x - 4\).

I eksempel 1, 2 og 3 utførte vi polynomdivisjon som ikke ga noen rest fordi \((x - x_1)\) var en faktor i polynomet. I eksempel 4 fikk vi en rest som betydde at \((x - x_1)\) ikke var en faktor i polynomet. Basert på eksemplene, kan vi formulere en setning:

Setning: Polynomdivisjonen \(f(x) : (x - x_1)\)

Gitt et polynom \(f\), vil polynomdivisjonen \(f(x) : (x - x_1)\) alltid kunne skrives på formen

\[ \dfrac{f(x)}{x - x_1} = K(x) + \dfrac{R}{x - x_1} \]

der \(R\) er resten i divisjonen og \(K(x)\) er et polynom som kalles for kvotienten.

---

Setningen over har noen konsekvenser vi skal utforske videre:

Utforsk 1

En tredjegradsfunksjon \(f\) er gitt ved

\[ f(x) = x^3 + 4x^2 + x - 6. \]

a

Regn ut \(f(-1)\).

Fasit

\[ f(-1) = -4 \]

b

Regn ut polynomdivisjonen

\[ (x^3 + 4x^2 + x - 6) : (x + 1) \]

Sammenlikn resten med svaret ditt fra a.

Fasit

Vi kan merke oss at resten \(R = -4\) og \(f(-1) = -4\). Altså er resten i \((x + 1)\) og \(f(-1)\) den samme.

---

Observasjonene gjort i Utforsk 1 lar oss skrive en setning som er viktig for polynomdivisjon:

Setning: Resten i polynomdivisjon med \((x - x_1)\)

Gitt et polynom \(f\), så er resten \(R\) i polynomdivisjon \(f(x) : (x - x_1)\) lik \(R = f(x_1)\).

Hvis \(R = 0\), betyr det at \(f(x_1) = 0\) og \((x - x_1)\) er en faktor i \(f(x)\).

Bevis

Ved polynomdivisjon \(f(x) : (x - x_1)\) får vi generelt

\[\begin{align*} \dfrac{f(x)}{x - x_1} &= K(x) + \dfrac{R}{x - x_1} \\ \\ \textcolor{red}{(x - x_1)} \cdot\dfrac{f(x)}{x - x_1} &= K(x) \cdot \textcolor{red}{(x - x_1)} + \dfrac{R}{x - x_1} \cdot \textcolor{red}{(x - x_1)} \\ \\ f(x) &= K(x) \cdot (x - x_1) + R \\ \end{align*}\]

Setter vi inn \(x = x_1\) i den siste likningen, får vi

\[ f(x_1) = K(x_1) \cdot (x_1 - x_1) + R = R. \]

Altså er resten \(R = f(x_1)\) og vi har bevist setningen.

---

Hjelpesetning: Resten i polynomdivisjonen \(f(x) : (x - x_1)\)

Hvis resten i polynomdivisjonen \(f(x) : (x - x_1)\) er \(R = f(x_1) = 0\), så er

• \(x = x_1\) et nullpunkt for \(f\) siden \(f(x_1) = 0\).

• \((x - x_1)\) er en faktor i \(f(x)\).

• \(f(x)\) er delelig med \((x - x_1)\). Noen ganger sier vi at polynomdivisjonen \(f(x) : (x - x_1)\) “går opp” og vi skriver \((x - x_1) \, | \, f(x)\) og leser det som “\((x - x_1)\) deler \(f(x)\)”.

Setningene over lar oss gjøre to ting:

• Avgjøre om et punkt \(x = x_1\) er et nullpunkt for \(f\), og dermed faktorisere \(f\).

• Regne ut funksjonsverdier \(f(x_1)\) raskt ved å dele med \((x - x_1)\) og lese av resten \(R\).

Vi tar et eksempel som illustrer setningen i praksis:

Eksempel 4

Et tredjegradspolynom \(f\) er gitt ved

\[ f(x) = x^3 - 2x^2 - 5x + 6. \]

Regn ut \(f(-1)\) ved hjelp av polynomdivisjon.

Løsning

Vi utfører polynomdivisjon og får:

Resten i polynomdivisjonen er \(8\), og derfor er \(f(-1) = 8\).

---

Horner-skjema

Når du leste gjennom eksempel 4 kan du ha stusset litt over en ting – hvordan i alle dager er dette mindre regning enn å bare sette inn verdien for \(x\) i \(f(x)\)? Trikset her er at vi gjør svært mye unødvendig skriving når vi gjør polynomdivisjonen – vi kan heller bare holde styr på koeffisientene og fokusere på de viktige regnestykkene som vi skal vise i neste eksempel:

Vi skal ta i bruk noe vi kaller for et Horner-skjema for å utføre divisjonen.

Horner-skjema

Et Horner-skjema kan brukes til å regne ut polynomdivisjonen \(f(x) : (x - x_1)\). La

\[ f(x) = a_3x^3 + a_2x^2 + a_1x + a_0 \]

og \(K(x)\) være kvotienten i polynomdivisjonen gitt ved

\[ K(x) = b_2x^2 + b_1x + b_0. \]

Da kan vi bestemme koeffisientene til \(K(x)\) og resten \(R\) ved å lage et Horner-skjema som vist nedenfor:

\[\begin{split} \begin{array}{r|cccc} & a_3 & a_2 & a_1 & a_0 \\ % Dividend coefficients x = x_1 & & b_2\cdot x_1 & b_1\cdot x_1 & b_0\cdot x_1 \\ % Linear term \hline & b_2 & b_1 & b_0 & R \\ % Resulting coefficients \end{array} \end{split}\]

der \(b_2 = a_3\) og de resterende tallene \(b_1, b_0\) og \(R\) regnes ut ved å summere tallene i kolonnen over streken. Vi jobber oss gjennom én og én kolonne fra venstre mot høyre.

Det viktigste å merke seg med den generelle teorien er hvor koeffisientene til telleren \(f(x)\) plasseres, og hvor koeffisientene til kvotienten \(K(x)\) og resten \(R\) plasseres. Rent praktisk trenger vi ikke huske formlene som står i hver kolonne – det hele blir klart med et eksempel.

Eksempel 5

Polynomdivisjonen fra eksempel 4 krever mye skriving:

Vi kan se at mange av leddene forsvinner som en trapp, så vi trenger ikke holde styr på de leddene. Rent praktisk lager vi Horner-skjemaet slik:

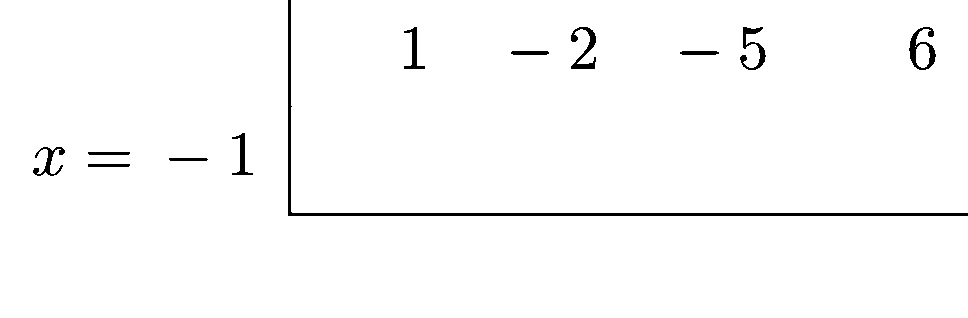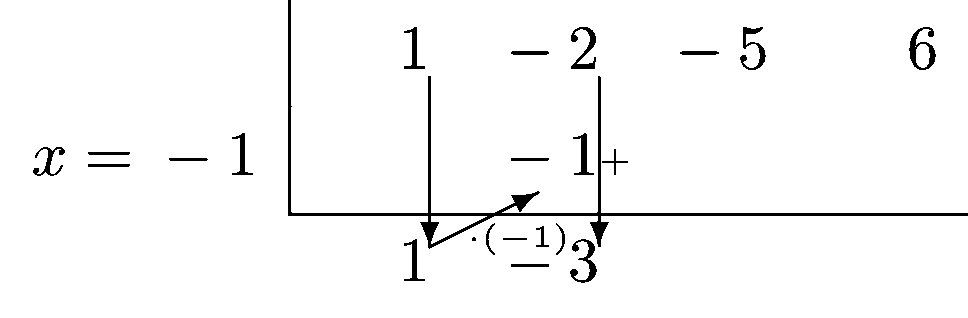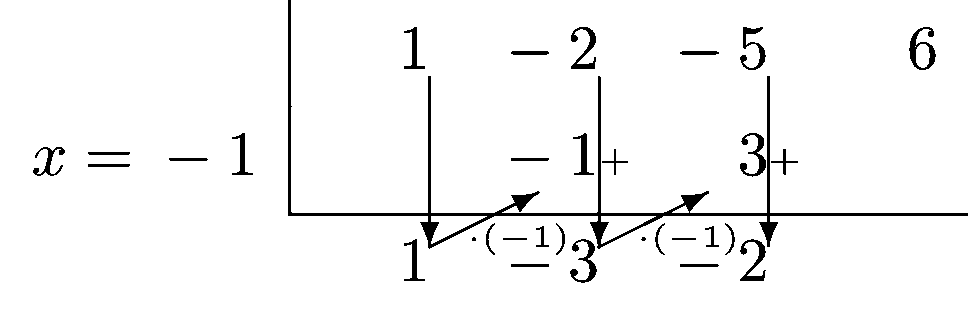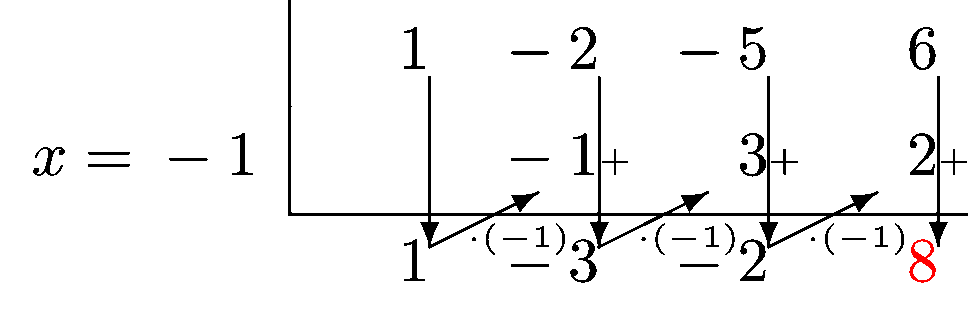
Fig. 21.1 viser hvordan vi algoritmisk regner ut verdiene i tabellen.

Prøv å sammenligne med polynomdivisjonen for å gjenkjenne hvor tallene i Horner-skjemaet dukker opp i polynomdivisjonen.

Vi kan oppsummere resultatet vi fikk med Horner-skjemaet som

Basert på Horner-skjemaet kan vi derfor lese av at

\[ K(x) = x^2 - 3x - 2 \quad \text{og} \quad R = 8. \]

Slår vi det hele sammen finner vi derfor at

\[ (x^3 - 2x^2 - 5x + 6) : (x + 1) = x^2 - 3x - 2 + \dfrac{8}{x + 1} \]

---

Underveisoppgave 1

Bruk et Horner-skjema til å regne ut kvotienten \(K(x)\) og resten \(R\) i polynomdivisjonen

\[ (x^3 - 4x^2 + 3x - 2) : (x - 2). \]

Fasit

Kvotienten:

\[ K(x) = x^2 - 2x - 1 \]

Rest:

\[ R = -4 \]

Løsning

Kvotienten:

\[ K(x) = x^2 - 2x - 1 \]

Rest:

\[ R = -4 \]