Oppgaver: Vekstfart

Oppgaver: Vekstfart#

Oppgave 1

a

Grafen til en andregradsfunksjon $f$ er vist i figuren nedenfor.

Bestem den gjennomsnittlige vekstfarten til $f$ i intervallet $[0, 3]$.

Fasit

\[ \frac{f(3) - f(0)}{3 - 0} = 1 \]

Løsning

Vi ser fra grafen til $f$ at $f(0) = -3$ og $f(3) = 0$. Den gjennomsnittlige vekstfarten til $f$ i intervallet $[0, 3]$ er gitt ved

\[ \frac{f(3) - f(0)}{3 - 0} = \frac{0 - (-3)}{3 - 0} = \frac{3}{3} = 1. \]

b

Grafen til en andregradsfunksjon $g$ er vist i figuren nedenfor.

Bestem den gjennomsnittlige vekstfarten til $g$ i intervallet $[-2, 2]$.

Fasit

\[ \frac{g(2) - g(-2)}{2 - (-2)} = 2 \]

Løsning

Vi ser fra grafen til $g$ at $g(-2) = -4$ og $g(2) = 4$. Den gjennomsnittlige vekstfarten til $g$ i intervallet $[-2, 2]$ er gitt ved

\[ \frac{g(2) - g(-2)}{2 - (-2)} = \frac{4 - (-4)}{2 - (-2)} = \frac{8}{4} = 2. \]

c

Grafen til en andregradsfunksjon $h$ er vist i figuren nedenfor.

Bestem den gjennomsnittlige vekstfarten til $h$ i intervallet $[-3, 3]$.

Fasit

\[ \frac{h(3) - h(-3)}{3 - (-3)} = 0 \]

Løsning

Fra grafen til $h$ ser vi at $h(-3) = 5$ og $h(3) = 5$. Den gjennomsnittlige vekstfarten til $h$ i intervallet $[-3, 3]$ er gitt ved

\[ \frac{h(3) - h(-3)}{3 - (-3)} = \frac{5 - 5}{3 - (-3)} = \frac{0}{6} = 0. \]

d

Grafen til en andregradsfunksjon $p$ er vist i figuren nedenfor.

Bestem den gjennomsnittlige vekstfarten til $p$ i intervallet $[-4, 1]$.

Fasit

\[ \frac{p(1) - p(-4)}{1 - (-4)} = 1 \]

Løsning

Fra grafen til $p$ ser vi at $p(-4) = 0$ og $p(1) = 5$. Den gjennomsnittlige vekstfarten til $p$ i intervallet $[-4, 1]$ er gitt ved

\[ \frac{p(1) - p(-4)}{1 - (-4)} = \frac{5 - 0}{1 - (-4)} = \frac{5}{5} = 1. \]

Oppgave 2

a

En andregradsfunksjon $f$ er gitt ved

\[ f(x) = x^2 - 4x + 5 \]

Bestem den gjennomsnittlige vekstfarten til $f$ i intervallet $[1, 3]$.

Fasit

\[ \frac{f(3) - f(1)}{3 - 1} = 0 \]

Løsning

Vi bestemmer $f(1)$ og $f(3)$:

\[\begin{align*} f(1) &= 1^2 - 4 \cdot 1 + 5 = 1 - 4 + 5 = 2, \\ \\ f(3) &= 3^2 - 4 \cdot 3 + 5 = 9 - 12 + 5 = 2. \end{align*}\]

Den gjennomsnittlige vekstfarten til $f$ i intervallet $[1, 3]$ er gitt ved

\[ \frac{f(3) - f(1)}{3 - 1} = \frac{2 - 2}{3 - 1} = \frac{0}{2} = 0. \]

b

En andregradsfunksjon $g$ er gitt ved

\[ g(x) = (x - 1)^2 - 4 \]

Bestem den gjennomsnittlige vekstfarten til $g$ i intervallet $[0, 2]$.

Fasit

\[ \frac{g(2) - g(0)}{2 - 0} = 0 \]

Løsning

Vi bestemmer $g(0)$ og $g(2)$:

\[\begin{align*} g(0) &= (0 - 1)^2 - 4 = 1 - 4 = -3, \\ \\ g(2) &= (2 - 1)^2 - 4 = 1 - 4 = -3. \end{align*}\]

Den gjennomsnittlige vekstfarten til $g$ i intervallet $[0, 2]$ er gitt ved

\[ \frac{g(2) - g(0)}{2 - 0} = \frac{-3 - (-3)}{2 - 0} = \frac{0}{2} = 0. \]

c

En andregradsfunksjon $h$ er gitt ved

\[ h(x) = (x - 1)(x + 2) \]

Bestem den gjennomsnittlige vekstfarten til $h$ i intervallet $[0, 1]$.

Fasit

\[ \frac{h(1) - h(0)}{1 - 0} = 2 \]

Løsning

Vi bestemmer $h(0)$ og $h(1)$:

\[\begin{align*} h(0) &= (0 - 1)(0 + 2) = -1 \cdot 2 = -2, \\ \\ h(1) &= (1 - 1)(1 + 2) = 0 \cdot 3 = 0. \end{align*}\]

Den gjennomsnittlige vekstfarten til $h$ i intervallet $[0, 1]$ er gitt ved

\[ \frac{h(1) - h(0)}{1 - 0} = \frac{0 - (-2)}{1 - 0} = \frac{2}{1} = 2. \]

d

En andregradsfunksjon $p$ er gitt ved

\[ p(x) = x^2 - 2x \]

Bestem den gjennomsnittlige vekstfarten til $p$ i intervallet $[-1, 1]$.

Fasit

\[ \frac{p(1) - p(-1)}{1 - (-1)} = -2 \]

Løsning

Vi bestemmer $p(-1)$ og $p(1)$:

\[\begin{align*} p(-1) &= (-1)^2 - 2 \cdot (-1) = 1 + 2 = 3, \\ \\ p(1) &= (1)^2 - 2 \cdot (1) = 1 - 2 = -1. \end{align*}\]

Den gjennomsnittlige vekstfarten til $p$ i intervallet $[-1, 1]$ er gitt ved

\[ \frac{p(1) - p(-1)}{1 - (-1)} = \frac{-1 - 3}{1 - (-1)} = \frac{-4}{2} = -2. \]

Oppgave 3

a

Grafen til den deriverte $f'$ til en andregradsfunksjon $f$ er vist i figuren nedenfor.

Bestem den momentane vekstfarten til $f$ i $(3, f(3))$.

Fasit

\[ f'(3) = 4 \]

Løsning

Vi ser at grafen til $f'$ går gjennom punktet $(3, 4)$. Den momentane vekstfarten til $f$ i punktet $(3, f(3))$ er $y$-koordinaten til punktet. Altså er

\[ f'(3) = 4 \]

b

Grafen til den deriverte $g'$ til en andregradsfunksjon $g$ er vist i figuren nedenfor.

Bestem stigningstallet til tangenten til grafen til $g$ i punktet $(-3, g(-3))$.

Fasit

\[ g'(-3) = 2 \]

Løsning

Vi ser at grafen til $g'$ går gjennom punktet $(-3, 2)$. Stigningstallet til tangenten til grafen til $g$ i punktet $(-3, g(-3))$ er $y$-koordinaten til punktet. Altså er

\[ g'(-3) = 2 \]

c

Grafen til den deriverte $h'$ til en andregradsfunksjon $h$ er vist i figuren nedenfor.

Bestem den momentane vekstfarten til $h$ i $(1, h(1))$.

Fasit

\[ h'(1) = -4 \]

Løsning

Vi ser at grafen til $h'$ går gjennom punktet $(1, -4)$. Den momentane vekstfarten til $h$ i punktet $(1, h(1))$ er $y$-koordinaten til punktet. Altså er

\[ h'(1) = -4 \]

d

Grafen til den deriverte $p'$ til en andregradsfunksjon $p$ er vist i figuren nedenfor.

Bestem stigningstallet til tangenten til grafen til $p$ i punktet $(-1, p(-1))$.

Fasit

\[ p'(-1) = 4 \]

Løsning

Vi ser at grafen til $p'$ går gjennom punktet $(-1, 4)$. Det er $y$-koordinaten til punktet som gir stigningstallet til tangenten til grafen til $p$ i punktet $(-1, p(-1))$. Altså er

\[ p'(-1) = 4 \]

Oppgave 4

a

Til høyre vises grafen til en andregradsfunksjon $f$.

Bestem hvilken av grafene nedenfor som viser grafen til den deriverte $f'$.

Fasit

Graf B.

b

Figuren til høyre vises grafen til en andregradsfunksjon $g$.

Bestem hvilken av grafene nedenfor som viser grafen til den deriverte $g'$.

Fasit

Graf D.

c

Figuren til høyre vises grafen til en andregradsfunksjon $h$.

Bestem hvilken av grafene nedenfor som viser grafen til den deriverte $h'$.

Fasit

Graf A.

d

Figuren til høyre vises grafen til en andregradsfunksjon $p$.

Bestem hvilken av grafene nedenfor som viser grafen til den deriverte $p'$.

Fasit

Graf B.

Oppgave 5

a

Grafen til $f'$ er vist i figuren til høyre.

Bestem hvilken av grafene nedenfor som viser grafen til $f$.

Fasit

Graf D.

b

Grafen til $g'$ er vist i figuren til høyre.

Bestem hvilken av grafene nedenfor som viser grafen til $g$.

Fasit

Graf C.

c

Grafen til $h'$ er vist i figuren til høyre.

Bestem hvilken av grafene nedenfor som viser grafen til $h$.

Fasit

Graf B.

d

Grafen til $p'$ er vist i figuren til høyre.

Bestem hvilken av grafene nedenfor som viser grafen til $p$.

Fasit

Graf C.

Oppgave 6

Bestem den deriverte til funksjonene.

a

\[ f(x) = x^2 - x + 1 \]

Fasit

\[ f'(x) = 2x - 1 \]

Løsning

Vi bruker formelen

\[ f'(x) = 2ax + b \]

Vi ser at $a = 1$ og $b = -1$. Dermed er

\[ f'(x) = 2 \cdot 1 \cdot x - 1 = 2x - 1. \]

b

\[ g(x) = -x^2 + 3x - 2 \]

Fasit

\[ g'(x) = -2x + 3 \]

Løsning

Vi bruker formelen

\[ g'(x) = 2ax + b \]

Vi ser at $a = -1$ og $b = 3$. Dermed er

\[ g'(x) = 2 \cdot (-1) \cdot x + 3 = -2x + 3. \]

c

\[ h(x) = 2x^2 + 1 \]

Fasit

\[ h'(x) = 4x \]

Løsning

Vi bruker formelen

\[ h'(x) = 2ax + b \]

Vi ser at $a = 2$ og $b = 0$. Dermed er

\[ h'(x) = 2 \cdot 2 \cdot x + 0 = 4x. \]

d

\[ p(x) = 3x^2 - 2x \]

Fasit

\[ p'(x) = 6x - 2 \]

Løsning

Vi bruker formelen

\[ p'(x) = 2ax + b \]

Vi ser at $a = 3$ og $b = -2$. Dermed er

\[ p'(x) = 2 \cdot 3 \cdot x - 2 = 6x - 2. \]

Oppgave 7

a

Grafen til den deriverte $f'$ til en andregradsfunksjon $f$ er vist i figuren nedenfor.

Punktet $P(1, 2)$ ligger på grafen til $f$.

Bestem likningen for tangenten til grafen til $f$ i punktet $P$.

../../../_images/a13.svg — Fig. 19.2 viser grafen til $f'$.#

Fasit

\[ y = -x + 3 \]

Løsning

Punktet på grafen til $f$ er $(1, 2)$. Det betyr at $f(1) = 2$.

Fra grafen til $f'$ ser vi at $f'(1) = -1$. Dette er stigningstallet til tangenten.

Vi bruker ettpunktsformelen til å bestemme likningen for tangenten:

\[ y = a(x - x_0) + y_0 = -1 \cdot (x - 1) + 2 = -x + 3. \]

b

Grafen til den deriverte $g'$ til en andregradsfunksjon $g$ er vist i figuren nedenfor.

Punktet $Q(-1, 1)$ ligger på grafen til $g$.

Bestem likningen for tangenten til grafen til $g$ i punktet $Q$.

../../../_images/b12.svg — Fig. 19.3 viser grafen til $g'$.#

Fasit

\[ y = 4x + 5 \]

Løsning

Punktet på grafen til $g$ er $(-1, 1)$. Det betyr at $g(-1) = 1$.

Fra grafen til $g'$ ser vi at $g'(-1) = 4$. Dette er stigningstallet til tangenten.

Vi bruker ettpunktsformelen til å bestemme likningen for tangenten:

\[ y = a(x - x_0) + y_0 = 4 \cdot (x - (-1)) + 1 = 4(x + 1) + 1 = 4x + 5. \]

c

Grafen til den deriverte $h'$ til en andregradsfunksjon $h$ er vist i figuren nedenfor.

Punktet $R(1, -3)$ ligger på grafen til $h$.

Bestem likningen for tangenten til grafen til $h$ i punktet $R$.

../../../_images/c13.svg — Fig. 19.4 viser grafen til $h'$.#

Fasit

\[ y = -2x - 1 \]

Løsning

Punktet på grafen til $h$ er $(1, -3)$. Det betyr at $h(1) = -3$.

Fra grafen til $h'$ ser vi at $h'(1) = -2$. Dette er stigningstallet til tangenten.

Vi bruker ettpunktsformelen til å bestemme likningen for tangenten:

\[ y = a(x - x_0) + y_0 = -2 \cdot (x - 1) - 3 = -2x + 2 - 3 = -2x - 1. \]

d

Grafen til den deriverte $p'$ til en andregradsfunksjon $p$ er vist i figuren nedenfor.

Punktet $S(-1, -2)$ ligger på grafen til $p$.

Bestem likningen for tangenten til grafen til $p$ i punktet $S$.

../../../_images/d10.svg — Fig. 19.5 viser grafen til $p'$.#

Fasit

\[ y = 3x + 1 \]

Løsning

Punktet på grafen til $p$ er $(-1, -2)$. Det betyr at $p(-1) = -2$.

Fra grafen til $p'$ ser vi at $p'(-1) = 3$. Dette er stigningstallet til tangenten.

Vi bruker ettpunktsformelen til å bestemme likningen for tangenten:

\[ y = a(x - x_0) + y_0 = 3 \cdot (x - (-1)) - 2 = 3(x + 1) - 2 = 3x + 1. \]

Oppgave 8

a

En andregradsfunksjon er gitt ved

\[ f(x) = x^2 - 3x + 1. \]

Bestem likningen for tangenten til grafen til $f$ i $(1, f(1))$.

Fasit

\[ y = -x \]

Løsning

Vi bestemmer $f(1)$:

\[ f(1) = 1^2 - 3 \cdot 1 + 1 = 1 - 3 + 1 = -1. \]

Altså er punktet på grafen til $f$ som tangenten går gjennom gitt ved $(1, -1)$.

For å finne stigningstallet til tangenten, må vi finne den deriverte $f(x)'$:

\[ f'(x) = 2x - 3. \]

Deretter regner vi ut stigningstallet i $x = 1$:

\[ f'(1) = 2 \cdot 1 - 3 = 2 - 3 = -1. \]

Så bruker vi ettpunktsformelen til å finne likningen for tangenten:

\[ y = a(x - x_0) + y_0 = -1 \cdot (x - 1) - 1 = -x + 1 - 1 = -x. \]

b

En andregradsfunksjon er gitt ved

\[ g(x) = -x^2 + 2x + 3. \]

Bestem likningen for tangenten til grafen til $g$ i $(-1, g(-1))$.

Fasit

\[ y = 4x + 4 \]

Løsning

Vi bestemmer $g(-1)$:

\[ g(-1) = -(-1)^2 + 2 \cdot (-1) + 3 = -1 - 2 + 3 = 0. \]

Altså er punktet på grafen til $g$ som tangenten går gjennom gitt ved $(-1, 0)$.

For å finne stigningstallet til tangenten, må vi finne den deriverte $g(x)'$:

\[ g'(x) = -2x + 2. \]

Deretter regner vi ut stigningstallet i $x = -1$:

\[ g'(-1) = -2 \cdot (-1) + 2 = 2 + 2 = 4. \]

Så bruker vi ettpunktsformelen til å finne likningen for tangenten:

\[ y = a(x - x_0) + y_0 = 4 \cdot (x - (-1)) + 0 = 4(x + 1) = 4x + 4. \]

c

En andregradsfunksjon er gitt ved

\[ h(x) = 2x^2 - x + 1. \]

Bestem likningen for tangenten til grafen til $h$ i $(2, h(2))$.

Fasit

\[ y = 7x - 7 \]

Løsning

Vi bestemmer $h(2)$:

\[ h(2) = 2 \cdot 2^2 - 2 + 1 = 2 \cdot 4 - 2 + 1 = 8 - 2 + 1 = 7. \]

Altså er punktet på grafen til $h$ som tangenten går gjennom gitt ved $(2, 7)$.

For å finne stigningstallet til tangenten, må vi finne den deriverte $h(x)'$:

\[ h'(x) = 4x - 1. \]

Deretter regner vi ut stigningstallet i $x = 2$:

\[ h'(2) = 4 \cdot 2 - 1 = 8 - 1 = 7. \]

Så bruker vi ettpunktsformelen til å finne likningen for tangenten:

\[ y = a(x - x_0) + y_0 = 7 \cdot (x - 2) + 7 = 7x - 14 + 7 = 7x - 7. \]

d

En andregradsfunksjon er gitt ved

\[ p(x) = \dfrac{1}{2}x^2 - 2 \]

Bestem likningen for tangenten til grafen til $p$ i $(4, p(4))$.

Fasit

\[ y = 4x - 10 \]

Løsning

Vi bestemmer $p(4)$:

\[ p(4) = \dfrac{1}{2} \cdot 4^2 - 2 = \dfrac{1}{2} \cdot 16 - 2 = 8 - 2 = 6. \]

Altså er punktet på grafen til $p$ som tangenten går gjennom gitt ved $(4, 6)$.

For å finne stigningstallet til tangenten, må vi finne den deriverte $p(x)'$:

\[ p'(x) = \dfrac{1}{2} \cdot 2x + 0 = x. \]

Deretter regner vi ut stigningstallet i $x = 4$:

\[ p'(4) = 4. \]

Så bruker vi ettpunktsformelen til å finne likningen for tangenten:

\[ y = a(x - x_0) + y_0 = 4 \cdot (x - 4) + 6 = 4x - 16 + 6 = 4x - 10. \]

Oppgave 9

a

En andregradsfunksjon $f$ er gitt ved

\[ f(x) = (x - 2)^2 + 1. \]

Hvilken av fortegnslinjene nedenfor viser fortegnslinja til $f'(x)$?

Fasit

Fortegnslinje A.

Løsning

Vi kan se at $f(x)$ er skrevet på ekstremalpunktsform med symmetrilinje $x = 2$. Det betyr at $f'(x) = 0$ når $x = 2$. Fortegnslinjene som viser denne egenskapen er A og B.

Vi kan se at $f(x)$ sin ledende koeffisient er $a = 1$, som er positiv. Dermed må grafen til $f$ være konveks (den smiler $\smile$). Da må grafen synke til venstre for symmetrilinja og stige til høyre for symmetrilinja. Det betyr at $f'(x) < 0$ til venstre for $x = 2$ og $f'(x) > 0$ til høyre for $x = 2$. Dette stemmer for fortegnslinje A.

b

En andregradsfunksjon $g$ er gitt ved

\[ g(x) = -2(x + 3)^2 + 4 \]

Hvilken av fortegnslinjene nedenfor viser fortegnslinja til $g'(x)$?

Fasit

Fortegnslinje D.

Løsning

Vi kan se at $g(x)$ er skrevet på ekstremalpunktsform med symmetrilinje $x = -3$. Det betyr at $g'(x) = 0$ når $x = -3$. Fortegnslinjene som viser denne egenskapen er B og D.

Vi kan se at $g(x)$ sin ledende koeffisient er $a = -2$, som er negativ. Dermed må grafen til $g$ være konkav (surt fjes $\frown$). Da må grafen stige til venstre for symmetrilinja og synke til høyre for symmetrilinja. Det betyr at $g'(x) > 0$ til venstre for $x = -3$ og $g'(x) < 0$ til høyre for $x = -3$. Dette stemmer for fortegnslinje D.

c

En andregradsfunksjon $h$ er gitt ved

\[ h(x) = -3(x + 2)(x - 4) \]

Hvilken av fortegnslinjene nedenfor viser fortegnslinja til $h'(x)$?

Fasit

Fortegnslinje C.

Løsning

Vi kan se at $h(x)$ er skrevet på nullpunktsform med nullpunkter i $x = -2$ og $x = 4$. Vi kan bestemme symmetrilinja ved å ta gjennomsnittet av nullpunktene:

\[ x_0 = \frac{-2 + 4}{2} = \frac{2}{2} = 1. \]

Det betyr at $h'(x) = 0$ når $x = 1$. Fortegnslinjene som viser denne egenskapen er B og C.

Vi kan se at $h(x)$ sin ledende koeffisient er $a = -3$, som er negativ. Dermed må grafen til $h$ være konkav (surt fjes $\frown$). Da må grafen stige til venstre for symmetrilinja og synke til høyre for symmetrilinja. Det betyr at $h'(x) > 0$ til venstre for $x = 1$ og $h'(x) < 0$ til høyre for $x = 1$. Dette stemmer for fortegnslinje C.

d

En andregradsfunksjon $p$ er gitt ved

\[ p(x) = x^2 + 4x + 3 \]

Hvilken av fortegnslinjene nedenfor viser fortegnslinja til $p'(x)$?

Fasit

Fortegnslinje B.

Løsning

Vi kan se at $p(x)$ er skrevet på standardform med $a = 1$ og $b = 4$. Vi kan bestemme symmetrilinja ved å bruke formelen

\[ x_0 = -\frac{b}{2a} = -\frac{4}{2 \cdot 1} = -\frac{4}{2} = -2 \]

Det betyr at $p'(x) = 0$ når $x = -2$. Fortegnslinjene som viser denne egenskapen er A og B.

Vi kan se at $p(x)$ sin ledende koeffisient er $a = 1$, som er positiv. Dermed må grafen til $p$ være konveks (den smiler $\smile$). Da må grafen synke til venstre for symmetrilinja og stige til høyre for symmetrilinja. Det betyr at $p'(x) < 0$ til venstre for $x = -2$ og $p'(x) > 0$ til høyre for $x = -2$. Dette stemmer for fortegnslinje B.

Oppgave 10

Figuren nedenfor viser grafen til en andregradsfunksjon $f$.

Om grafen til $f$ får du vite at

Grafen til $f$ skjærer $x$-aksen i $(3, 0)$.
En tangent med likningen $y = 2x + 3$ skjærer grafen til $f$ og $y$-aksen i samme punkt.

Bestem $f(x)$ og $f'(x)$.

Fasit

\[ f(x) = -x^2 + 2x + 3 \qog f'(x) = -2x + 2. \]

Løsning

Vi velger å skrive $f(x)$ på standardform:

\[ f(x) = ax^2 + bx + c \]

Vi kan se at grafen til $f$ skjærer $x$-aksen i $(3, 0)$ som betyr at $f(3) = 0$.

Tangenten skjærer $y$-aksen i punktet $(0, 3)$ og siden grafen til $f$ skjærer gjennom samme punkt, så må $f(0) = 3$.

Tangenten har stigningstall $2$ som betyr at den momentane vekstfarten til $f$ i punktet $(0, 3)$ er $f'(0) = 2$.

Dermed har vi tre likninger:

\[\begin{align*} f(0) &= 3 && \text{Skjæringspunkt med $y$-aksen}\\ \\ f(3) &= 0 && \text{Skjæringspunkt med $x$-aksen}\\ \\ f'(0) &= 2 && \text{Stigningstall til tangenten i $(0, f(0))$} \end{align*}\]

Vi bruker CAS til å bestemme $a$, $b$ og $c$ ved å løse likningssystemet:

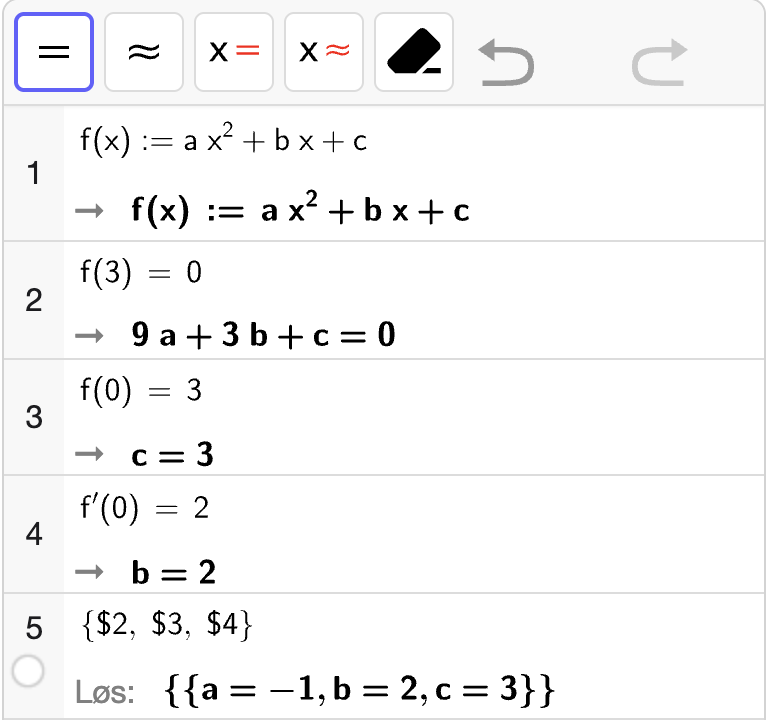
Fra utskriften ser vi at

\[ a = -1 \and b = 2 \and c = 3. \]

Det betyr at

\[ f(x) = -x^2 + 2x + 3 \qog f'(x) = -2x + 2. \]

Oppgave 11

I figuren nedenfor vises grafen til en andregradsfunksjon $f$.

Grafen til $f$ har

En tangent i punktet $(-1, f(-1))$ har likningen $y = 4x + 9$
En tangent i punktet $(2, f(2))$ har stigningstall $-2$.

Bestem $f(x)$ og $f'(x)$.

Fasit

\[ f(x) = -x^2 + 2x + 8 \qog f'(x) = -2x + 2. \]

Løsning

Vi velger å skrive $f(x)$ på standardform:

\[ f(x) = ax^2 + bx + c. \]

Tangenten i $(-1, f(-1))$ har likningen $y = 4x + 9$. Tangenten og grafen til $f$ må ha samme $y$-koordinat når $x = -1$. Det betyr at

\[ f(-1) = 4 \cdot (-1) + 9 = -4 + 9 = 5. \]

Tangenten har stigningstall $4$ som betyr at den momentane vekstfarten til $f$ i punktet $(-1, f(-1))$ er $f'(-1) = 4$.

Tangenten i $(2, f(2))$ har stigningstall $-2$ som betyr at den momentane vekstfarten til $f$ i punktet $(2, f(2))$ er $f'(2) = -2$.

Dermed har vi tre likninger:

\[\begin{align*} f(-1) &= 5 && \text{Punktet $(-1, f(-1))$ den ene tangenten går gjennom}\\ \\ f'(-1) &= 4 && \text{Stigningstall til tangenten i $(-1, f(-1))$}\\ \\ f'(2) &= -2 && \text{Stigningstall til tangenten i $(2, f(2))$}\\ \end{align*}\]

Vi bruker CAS til å bestemme $a$, $b$ og $c$ ved å løse likningssystemet:

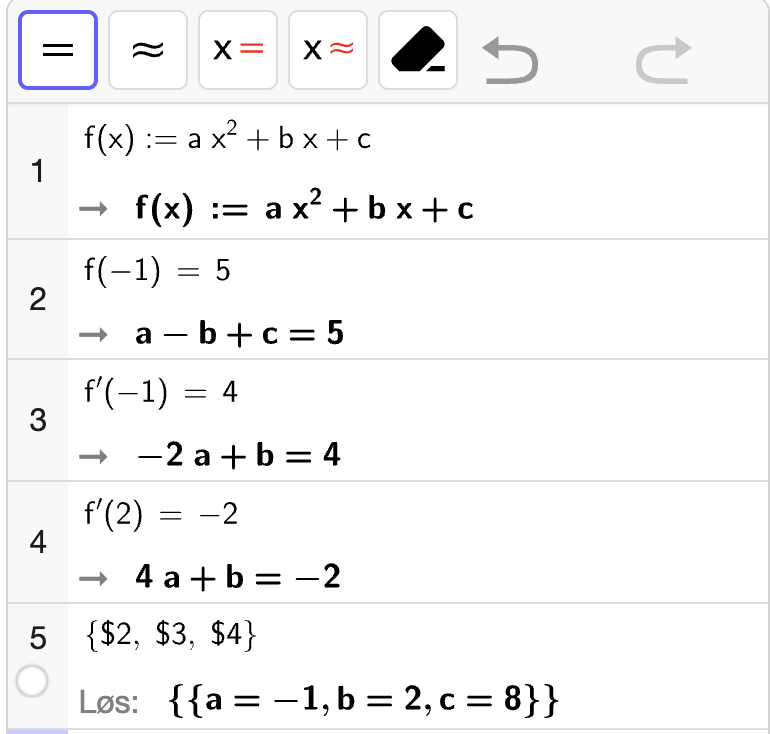
Fra utskriften ser vi at

\[ a = -1 \and b = 2 \and c = 8. \]

Det betyr at

\[ f(x) = -x^2 + 2x + 8 \qog f'(x) = -2x + 2. \]

Oppgave 12

I figuren nedenfor vises grafen til en andregradsfunksjon $f$.

Grafen til $f$ har

En tangent i punktet $(x_1, 2)$ med likningen $y = -2x - 4$.
En tangent i punktet $(1, f(1))$ med stigningstall $6$.

Bestem $f(x)$ og $f'(x)$.

Fasit

\[ f(x) = x^2 + 4x + 5 \qog f'(x) = 2x + 4. \]

Løsning

Vi velger å skrive $f(x)$ på standardform:

\[ f(x) = ax^2 + bx + c. \]

Vi kan bestemme $x$-koordinaten til punktet tangenten som går gjennom $(x_1, 2)$ treffer ved å sette likningen til tangenten lik $2$ og løse for $x$:

\[ -2x - 4 = 2 \liff -2x = 6 \liff x = -3. \]

Altså går tangenten gjennom punktet $(-3, 2)$ på grafen til $f$. Det betyr at $f(-3) = 2$.

Tangenten som går gjennom $(-3, 2)$ har stigningstall $-2$ som betyr at $f'(-3) = -2$.

Tangenten i $(1, f(1))$ har stigningstall $6$ som betyr at $f'(1) = 6$.

Dermed har vi tre likninger:

\[\begin{align*} f(-3) &= 2 && \text{Punktet $(-3, 2)$ den ene tangenten går gjennom}\\ \\ f'(-3) &= -2 && \text{Stigningstall til tangenten i $(-3, 2)$}\\ \\ f'(1) &= 6 && \text{Stigningstall til tangenten i $(1, f(1))$}\\ \end{align*}\]

Vi bruker CAS til å bestemme $a$, $b$ og $c$ ved å løse likningssystemet:

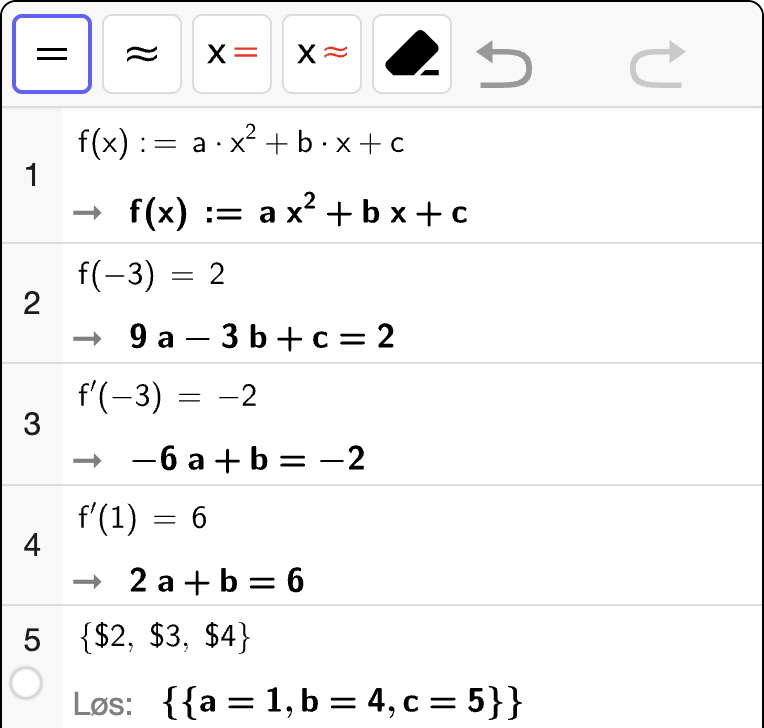
Fra utskriften ser vi at

\[ a = 1 \and b = 4 \and c = 5. \]

Dermed er

\[ f(x) = x^2 + 4x + 5 \qog f'(x) = 2x + 4. \]

Oppgave 13

Grafen til en andregradsfunksjon $f$ er vist nedenfor.

Om andregradsfunksjonen $f$ får du vite at

Tangenten i punktet $(-2, 0)$ har likningen $y = 9x + 18$
Tangenten i punktet $(8, -10)$ har likningen $y = -11x + 78$

Bestem $f'(x)$.

Fasit

\[ f'(x) = -2x + 5 \]

Løsning

Vi vet at $f'(x)$ er en lineær funksjon. Vi kan velge å skrive $f'(x)$ på ettpunktsform:

\[ f'(x) = a(x - x_0) + y_0 \]

Så må vi bestemme stigningstallet $a$ og ett punkt $(x_0, y_0)$ på grafen til $f'$.

Tangenten som går gjennom punktet $(-2, 0)$ på grafen til $f$ har likningen $y = 9x + 18$. Det betyr at $x$-koordinaten til punktet er $x = -2$ og $y$-koordinaten til $f'$ er $y = 9$ siden det er stigningstallet til tangenten. Dermed er punktet $(-2, 9)$ på grafen til $f'$.

Tangenten som går gjennom punktet $(8, -10)$ på grafen til $f$ har likningen $y = -11x + 78$. Det betyr at $x$-koordinaten til punktet er $x = 8$ og $y$-koordinaten til $f'$ er $y = -11$. Dermed er punktet $(8, -11)$ på grafen til $f'$.

Vi har nå to punkter på grafen til $f'$, så vi kan bestemme stigningstallet $a$:

\[ a = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-11 - 9}{8 - (-2)} = \frac{-20}{10} = -2. \]

Så kan vi bruke ett av punktene til å bestemme $f'(x)$. Vi velger $(-2, 9)$:

\[ f'(x) = -2(x - (-2)) + 9 = -2(x + 2) + 9 = -2x - 4 + 9 = -2x + 5. \]

Oppgave 14

Grafen til en andregradsfunksjon $f$ er vist i figuren nedenfor.

To tangenter til grafen til $f$ går gjennom punktene $(1, f(1))$ og $(3, f(3))$.

Tangenten i $(1, f(1))$ har stigningstall $1$
Tangenten i $(3, f(3))$ har stigningstall $-3$

a

Grafen til en andregradsfunksjon $f$ er vist i figuren nedenfor.

To tangenter til grafen til $f$ går gjennom punktene $(1, f(1))$ og $(3, f(3))$.

Tangenten i $(1, f(1))$ har stigningstall $1$
Tangenten i $(3, f(3))$ har stigningstall $-3$

Bestem $f'(x)$.

Fasit

\[ f'(x) = -2x + 3. \]

Løsning

Vi vet at $f'(x)$ er en lineær funksjon. Vi kan velge å skrive $f'(x)$ på ettpunktsform:

\[ f'(x) = a(x - x_0) + y_0 \]

Så må vi bestemme stigningstallet $a$ og ett punkt $(x_0, y_0)$ på grafen til $f'$. Vi vet at tangenten som går gjennom punktet $(1, f(1))$ har stigningstall $1$, så punktet $(1, 1)$ ligger på grafen til $f'$.

Tangenten som går gjennom punktet $(3, f(3))$ har stigningstall $-3$, så punktet $(3, -3)$ ligger på grafen til $f'$.

Vi har nå to punkter på grafen til $f'$, så vi kan bestemme stigningstallet $a$:

\[ a = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-3 - 1}{3 - 1} = \frac{-4}{2} = -2. \]

Så kan vi bruke ett av punktene til å bestemme $f'(x)$. Vi velger $(1, 1)$:

\[ f'(x) = -2(x - 1) + 1 = -2x + 2 + 1 = -2x + 3. \]

b

Tangentene skjærer hverandre i punktet $(2, 4)$.

Bestem $f(x)$.

Fasit

\[ f(x) = -x^2 + 3x + 1. \]

Løsning

Tangenten i $(1, f(1))$ har stigningstall $1$. Siden den skjærer den andre tangenten i $(2, 4)$, vil $y$-koordinaten til tangenten være $f(1) = 3$ siden den stiger med $1$ fra $x = 1$ til $x = 2$.

Vi vet allerede at

\[ f'(x) = -2x + 3. \]

Vi vet også sammenhengen mellom $f(x)$ og $f'(x)$ er gitt ved

\[ f(x) = ax^2 + bx + c \limplies f'(x) = 2ax + b. \]

Det betyr at

\[ 2a = -2 \and b = 3 \liff a = -1 \and b = 3. \]

Altså er $f(x)$ på formen

\[ f(x) = -x^2 + 3x + c. \]

For å bestemme $x$, setter vi opp en likningen med $f(1) = 3$:

\[ f(1) = 3 \liff -1 \cdot 1^2 + 3 \cdot 1 + c = 3 \]

som vi forenkler til

\[ -1 + 3 + c = 3 \liff c = 1. \]

Dermed er

\[ f(x) = -x^2 + 3x + 1. \]

Oppgave 15

Nedenfor vises grafen til en andregradsfunksjon $f$ og to tangenter som skjærer gjennom nullpunktene til $f$.

Den ene tangenten har stigningstall $4$.
Tangentene skjærer hverandre i $(-1, -8)$.

Bestem $f(x)$ og $f'(x)$.

Fasit

\[ f(x) = x^2 + 2x - 3 \qog f'(x) = 2x + 2. \]

Løsning

Vi velger å skrive $f(x)$ på standardform:

\[ f(x) = ax^2 + bx + c. \]

Tangenten som går gjennom det positive nullpunktet er tangenten som må ha stigningstall $4$. Siden den andre tangenten går gjennom det andre nullpunktet til $f$, betyr det at den må ha stigningstall $-4$ på grunn av symmetrien til andregradsfunksjoner.

Tar vi utgangspunkt i tangenten med stigningstall $4$, så vil den skjære $x$-aksen i $x = 1$ siden den går gjennom punktet $(-1, -8)$ og har stigningstall $4$. Det følger fordi $y$-verdien øker med $4$ for hver gang vi øker $x$ med $1$.

Tilsvarende vil den andre tangenten med stigningstall $-4$ skjære $x$-aksen i $x = 3$ siden den går gjennom punktet $(-1, -8)$ og har stigningstall $-4$. Det følger fordi $y$-verdien synker med $4$ for hver gang vi øker $x$ med $1$.

Nå har vi nok opplysninger til å sette opp tre likninger og bestemme $a$, $b$ og $c$:

\[\begin{align*} f(1) &= 0 && \text{Det positive nullpunktet til $f$}\\ \\ f'(1) &= -8 && \text{Stigningstallet til tangenten i $(1, 0)$}\\ \\ f(-3) &= 0 && \text{Det negative nullpunktet til $f$} \end{align*}\]

Vi løser likningssystemet i CAS:

Fra utskriften ser vi at

\[ a = 1 \and b = 2 \and c = -3 \]

Det betyr at

\[ f(x) = x^2 + 2x - 3 \qog f'(x) = 2x + 2. \]

Oppgave 16

I figuren nedenfor vises grafen til to lineære funksjoner $f$ og $g$. Punktene $A$ og $B$ og $C$ danner en likebeint trekant $\triangle ABC$ der sidelengden $AB = 4$.

Et rektangel har hjørnene $(-k, 0)$ og $(-k, g(-k))$ og $(k, f(k))$ og $(k, 0)$ der $k > 0$.

a

Bestem $f(x)$ og $g(x)$.

Fasit

\[\begin{align*} f(x) &= -(x - 2) \\ \\ g(x) &= x + 2 \end{align*}\]

Løsning

Trekanten er en likebeint trekant der vinkelen i toppunkt $C$ er $90\degree$. Siden trekanten er likebeint betyr det at vinkelen i hjørnene $A$ og $B$ er like store. Det betyr at vinkelene der er $45\degree$ siden vinkelsummen i en trekant $180\degree$.

Det følger at $A$ og $B$ er like langt unna $y$-aksen og siden $AB = 4$, må derfor

\[ A = (-2, 0) \qog B = (2, 0). \]

Hvis vi lar $O = (0, 0)$ være origo, så vil $\triangle OBC$ være en rettvinklet trekant med $45\degree$ vinkler som betyr at høyden $OC$ er like lang som grunnlinja $OB$. Dermed er $C = (0, 2)$.

Siden $f$ går gjennom punktene $C$ og $B$, kan vi finne stigningstallet til $f$ som følger:

\[ a = \dfrac{2 - 0}{0 - 2} = -1. \]

Siden $f$ har et nullpunkt i $B$, så kan skrive $f(x)$ på nullpunktsform:

\[ f(x) = a(x - x_1) = -1(x - 2) = -(x - 2). \]

Tilsvarende kan vi finne stigningstallet til $g$ som går gjennom $A$ og $C$:

\[ a = \dfrac{2 - 0}{0 - (-2)} = \dfrac{2}{2} = 1. \]

Siden $g$ har et nullpunkt i $A$, så kan skrive $g(x)$ på nullpunktsform:

\[ g(x) = a(x - x_1) = 1(x - (-2)) = (x + 2). \]

b

Lag en funksjon $A(k)$ for arealet av rektangelet uttrykt ved $k$.

Fasit

\[ A(k) = -2k^2 + 4k = -2k(k - 2). \]

Løsning

Grunnlinja til rektangelet er $2k$ og høyden er $f(k)$ (eller $g(-k)$ som vil ha samme verdi). Dermed er arealet av rektangelet gitt ved

\[ A(k) = 2k \cdot f(k) = 2k \cdot (-(k - 2)) = -2k^2 + 4k. \]

c

Bestem hvilken verdi av $k$ som gir størst mulig areal av rektangelet.

Hva er det største arealet?

Fasit

\[ k = 1 \qog A(1) = 2. \]

Løsning

Arealet $A(k)$ er en andregradsfunksjon som er konkav (surt fjes $\frown$) siden den har negativ ledende koeffisient. Da har den et toppunkt som vi kan bestemme ved å bruke formelen for symmetrilinja:

\[ k = -\frac{b}{2a} = -\frac{4}{2 \cdot (-2)} = -\frac{4}{-4} = 1. \]

Dermed er arealet av rektangelet størst hvis $k = 1$. Det største arealet er gitt ved $y$-koordinaten til toppunktet:

\[ A(1) = -2 \cdot 1^2 + 4 \cdot 1 = -2 + 4 = 2. \]

Oppgave 17

En arkitekt har tegnet et snitt av en lagerhall. Lagerhallen er 20 meter høy og har form som en parabel gitt ved

\[ p(x) = -\dfrac{1}{12}x^2 + 20 \]

På taket av lagerhallen skal det plasseres et webkamera. Webkameraet skal festet på en stang som er 3 meter lang.

Den rette linjen på figuren går gjennom punktet $(0, 23)$ og er en tangent til grafen.

a

Bestem likningen til tangenten.

Fasit

\[ y = -x + 23 \]

b

Hvor langt fra veggen på lagerhallen kan en tyv bevege seg uten å bli fotografert av webkameraet?

Fasit

Ca. 5.5 meter dersom en person er 2 meter høy.