Ikke-lineære likningssystemer

18. Ikke-lineære likningssystemer#

Læringsmål

  • Kunne løse ikke-lineære likningssystemer grafisk, algebraisk og med programmering.

Et ikke-lineært likningssystem består av to eller flere likninger der minst én av de ukjente variablene er en ikke-lineær potens. For eksempel hvis en av de ukjente i likningene er \(x^2\), så har vi et ikke-lineært likningssystem. Vi skal begrense oss til likningssystemer der vi har lineære eller kvadratiske potenser for de ukjente.

Akkurat som når vi jobbet med lineære likningssystemer, kan vi løse ikke-lineære likningssystemer med tre forskjellige strategier:

  1. Grafisk

  2. Algebraisk

  3. Med programmering

Grafisk løsning#

Når vi løser et ikke-lineært likningssystem grafisk, tegner vi grafene som svarer til likningene og finner skjæringspunktene mellom dem. Hvert skjæringspunkt representerer en løsning på likningssystemet.

La oss se på et eksempel:

Eksempel 1

Et likningssystem er gitt ved

\[\begin{align*} x^2 + y &= 3 \\ x - y &= 3 \end{align*}\]

Løsning

Den første likningen representerer en andregradsfunksjon som vi kan se ved å løse likningen for \(y\):

\[ x^2 + y = 3 \liff y = 3 - x^2 \]

Den andre likningen representerer en lineær funksjon som vi kan se ved å løse likningen for \(y\):

\[ x - y = 3 \liff y = x - 3 \]

Vi tegner grafene til hver av likningene og leser av skjæringspunktene for å bestemme løsningene:

../../../_images/figur8.svg

Vi ser at grafene skjærer hverandre i punktene \((2, -1)\) og \((-3, -6)\). For å beskrive løsningen, skriver vi:

\[ x = 2 \quad \underbrace{\land}_{\text{og samtidig}} \quad y = -1 \quad \overbrace{\lor}^{\text{eller}} \quad x = -3 \quad \underbrace{\land}_{\text{og samtidig}} \quad y = -6 \]

Uten annoteringer, skriver vi altså bare:

\[ x = 2 \and y = -1 \quad \lor \quad x = -3 \and y = -6 \]

Vi tolker dette som at enten så er \(x = 2\) og samtidig er \(y = -1\). Eller så er \(x = -3\) og samtidig er \(y = -6\).

Underveisoppgave 1

Et likningssystem er gitt ved

\[\begin{align*} x^2 + y &= 1 \\ x + y &= -1 \end{align*}\]

Grafene til de to likningene er vist i figuren nedenfor.

Bruk figuren til å løse likningssystemet.

../../../_images/figur9.svg

Fasit

\[ x = -1 \and y = 0 \or x = -3 \and y = 2 \]

Løsning

Grafene skjærer hverandre i punktene \((-1, 0)\) og \((-3, 2)\). Løsningen av likningssystemet er derfor

\[ x = -1 \and y = 0 \or x = -3 \and y = 2 \]

I praksis kan vi bruke graftegner til å tegne grafene og finne skjæringspunktene. La oss se på et eksempel.

Eksempel 2

Et likningssystem er gitt ved

\[\begin{align*} 2x - y &= 3 \\ x^2 - 2y - y &= 3 \end{align*}\]

Nedenfor ser du en gif som viser hvordan man løser likningen med grafvinduet i Geogebra. Vi trykker på GeoGebra mode_intersect icon (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktet.

../../../_images/grafisk_l%C3%B8sning1.gif

Skjæringspunktene mellom de to grafene er \((4, 5)\) og \((0, -3)\) som betyr at løsningen av likningssystemet er

\[ x = 4 \and y = 5 \or x = 0 \and y = -3 \]

Underveisoppgave 2

Et likningssystem er gitt ved

\[\begin{align*} 2x - y &= 1 \\ -x^2 + 3x + y &= 3 \end{align*}\]

Bruk Geogebra-vinduet nedenfor til å løse likningssystemet grafisk.

Fasit

\[ x = 1 \and y = 1 \or x = 4 \and y = 7 \]

Løsning

Vi skriver inn likningene i algebrafeltet og trykker først på GeoGebra mode_point icon for å få opp alternativer og deretter trykker på GeoGebra mode_intersect icon (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktene. Se figuren nedenfor.

../../../_images/sol1.png

Skjæringspunktene er \((1, 1)\) og \((4, 7)\) som betyr at løsningen av likningsystemet er

\[ x = 1 \and y = 1 \or x = 4 \and y = 7 \]

Algebraisk løsning#

Når vi løser et ikke-lineært likningssystem algebraisk, bruker vi oftest innsettingsmetoden som leder til en andregradslikning. La oss se på et eksempel:

Eksempel 3

Løs likningssystemet

\[\begin{align*} x^2 + y &= 3 \\ x - y &= 3 \end{align*}\]

Løsning

Vi starter med å løse likning 2 for \(y\):

\[ x - y = 3 \liff y = x - 3 \]

deretter setter vi inn dette for \(y\) i likning 1:

\[ x^2 + (x - 3) = 3 \liff x^2 + x - 6 = 0 \]

Deretter kan vi bruke \(abc\)-formelen for å løse likningen:

\[ x = \dfrac{-1 \pm \sqrt{1^2 - 4 \cdot 1 \cdot (-6)}}{2 \cdot 1} = \dfrac{-1 \pm \sqrt{25}}{2} = \dfrac{-1 \pm 5}{2} \]

som gir oss løsningene

\[ x = -3 \or x = 2. \]

For hver verdi av \(x\) får vi en verdi for \(y\). Vi bruker at \(y = x - 3\) og setter inn verdiene for \(x\). Når \(x = -3\), så får vi

\[ y = -3 - 3 = -6 \]

Når \(x = 2\), så får vi

\[ y = 2 - 3 = -1 \]

Dermed her løsningen av likningssystemet

\[ x = -3 \and y = -6 \or x = 2 \and y = -1 \]

Underveisoppgave 2

Løs likningssystemet nedenfor algebraisk.

\[\begin{align*} 2x - y &= 4 \\ x^2 - 3x - 2y &= -4 \end{align*}\]

Fasit

\[ x = 4 \and y = 4 \or x = 3 \and y = 2 \]

Løsning

Vi løser likning 1 for \(y\):

\[ 2x - y = 4 \liff y = 2x - 4 \]

Deretter setter vi inn dette for \(y\) i likning 2:

\[ x^2 - 3x - 2(2x - 4) = -4 \]

Så forenkler vi likningen så mye som mulig:

\[\begin{align*} x^2 - 3x - 4x + 8 &= -4 \\ \\ x^2 - 7x + 12 &= 0 \\ \\ \end{align*}\]

Nå kan vi bruke \(abc\)-formelen for å bestemme verdiene for \(x\):

\[ x = \dfrac{-(-7) \pm \sqrt{(-7)^2 - 4 \cdot 1 \cdot 12}}{2 \cdot 1} = \dfrac{7 \pm \sqrt{49 - 48}}{2} = \dfrac{7 \pm 1}{2} \]

Det gir oss løsningene

\[ x = 4 \or x = 3 \]

For hver verdi av \(x\) får vi en verdi for \(y\). Vi bruker at \(y = 2x - 4\) og setter inn verdiene for \(x\). Når \(x = 4\), så får vi

\[ y = 2 \cdot 4 - 4 = 8 - 4 = 4 \]

Når \(x = 3\), så får vi

\[ y = 2 \cdot 3 - 4 = 6 - 4 = 2 \]

Dermed er løsningen av likningssystemet

\[ x = 4 \and y = 4 \or x = 3 \and y = 2 \]

CAS#

Vi kan bruke CAS til å løse ikke-lineære likningssystemer på samme måte som vi gjorde med lineære likningssystemer. Det skal du se nærmere på i Utforsk 1.

Utforsk 1

I gif-en nedenfor vises det hvordan vi kan bruke CAS til å løse et ikke-lineært likningssystem.

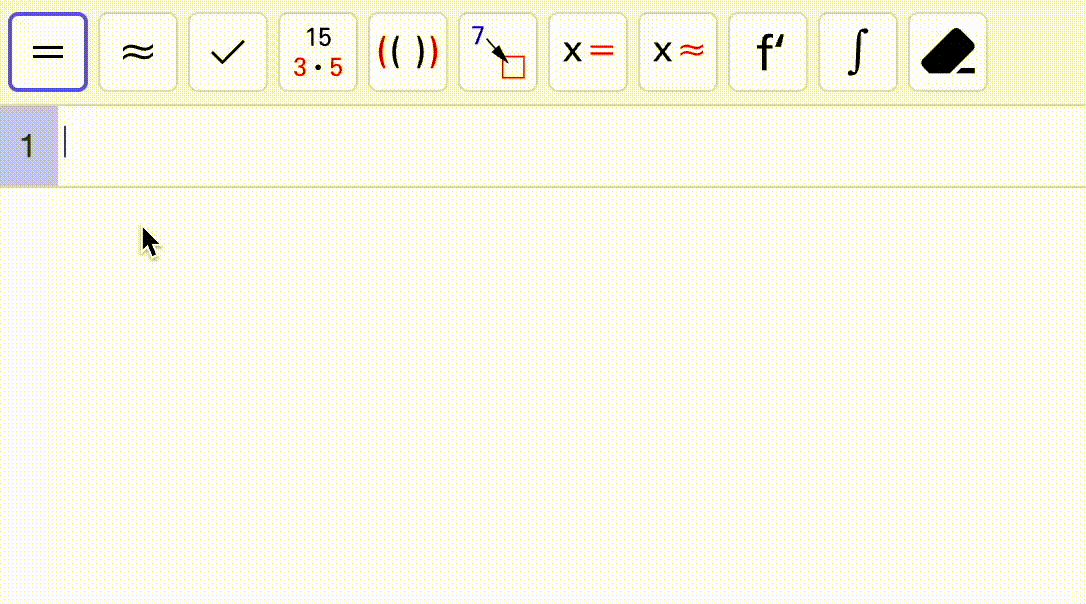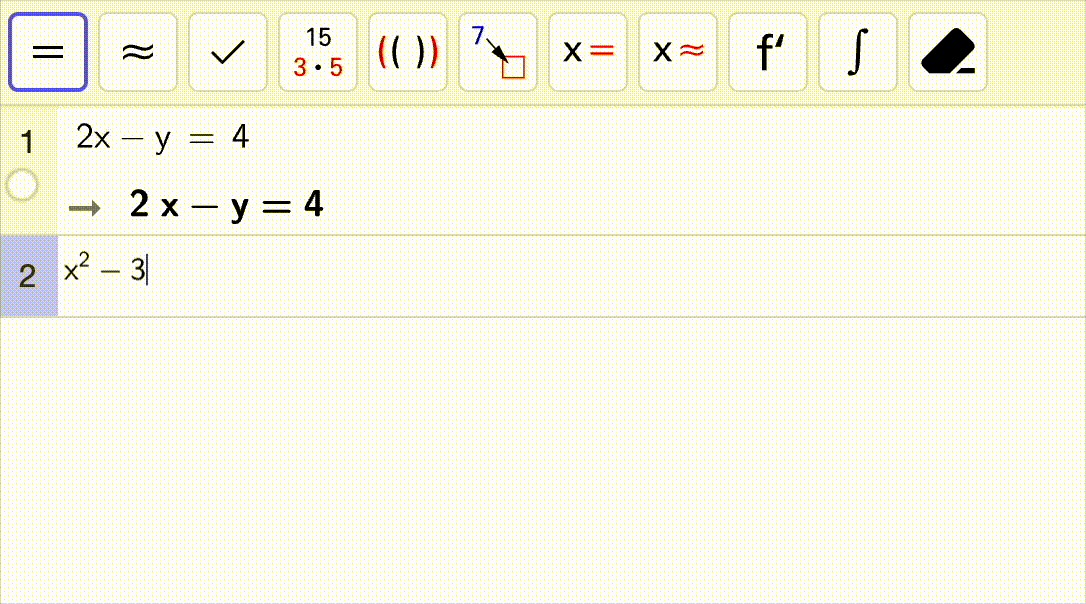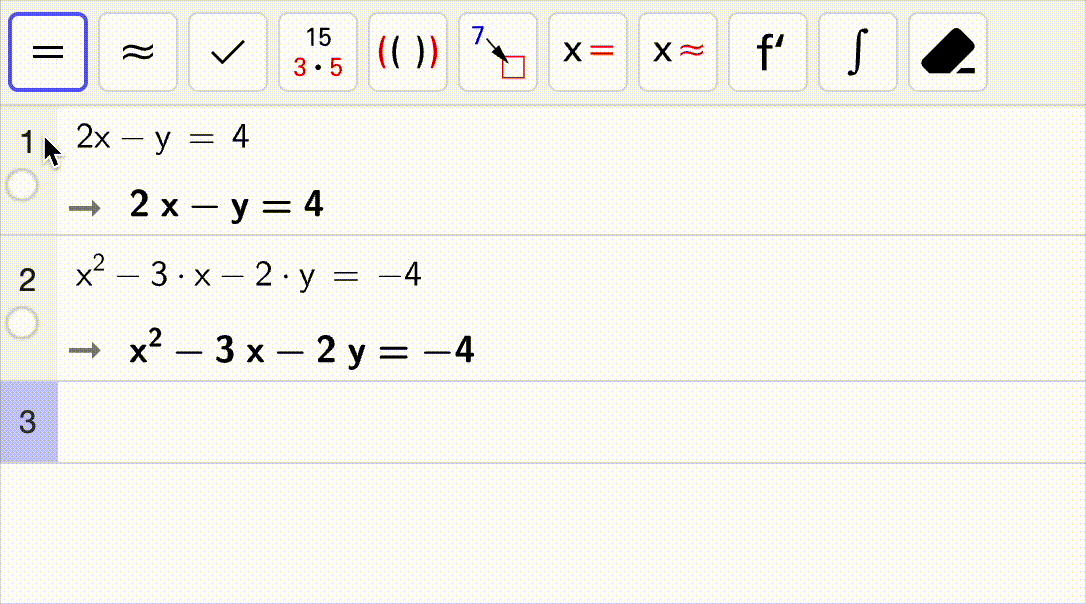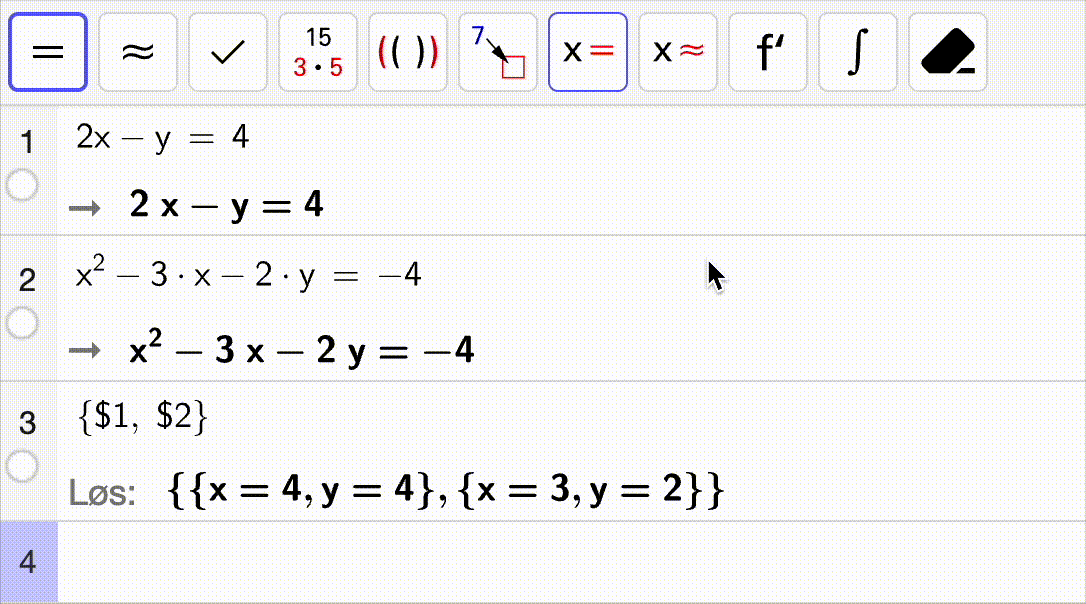
../../../_images/cas_likningssystemer.gif

Bruk CAS til å løse likningssystemet som er vist i gif-en.

Bruk CAS til å løse likningssystemet

\[\begin{align*} x - y &= 1\\ \\ -x^2 + 4x + y &= 3 \end{align*}\]

Bruk CAS til å løse likningssystemet

\[\begin{align*} -x^2 + 5x - y &= 6\\ \\ x + 2y &= -7 \end{align*}\]

Løsning med programmering#

Når vi løser en ikke-lineært likningssystem med programmering, kan vi bruke systematisk prøve ut punkter \((x, y)\) og sjekke om de oppfyller likningene i systemet.

Utforsk 2

Nedenfor vises et program som løser et likningssystem.

Bruk CAS til å forutsi utskriften til programmet og kjør det for å sjekke svaret ditt.

Endre på programmet og bruk det til å løse likningssystemet

\[\begin{align*} 2x + y &= 5 \\ \\ x^2 - 2x + 3y &= 3 \end{align*}\]

Løsning

1for x in range(-10, 11):
2    for y in range(-10, 11):
3        if 2*x + y == 5 and x**2 - 2*x + 3*y == 3:
4            print((x, y))

som gir utskriften

(2, 1)
(6, -7)

som betyr at løsningen av likningessystemet er

\[ x = 2 \and y = 1 \or x = 6 \and y = -7 \]
Innhold