31. Cosinussetningen#
Læringsmål
Kunne bruke cosinussetningen til å regne ut ukjente sider og vinkler i en trekant.
Kunne begrunne cosinussetningen.
Cosinussetningen er en generalisert versjon av Pytagoras’ setning som gjelder for alle trekanter. Vi skal se hvordan vi kommer fram til setningen senere, samt hvordan Pytagoras’ setning kan betraktes som et spesialtilfelle av cosinussetningen.
Vi starter med å se på hva cosinussetningen sier.
Cosinussetningen
En trekant \(\triangle ABC\) er vist nedenfor.
Da gjelder følgende:
Underveisoppgave 1
Nedenfor vises en trekant \(\triangle ABC\).
Bestem \(AC\) ved hjelp av cosinussetningen.
Fasit
Løsning
Siden vi kjenner til vinkelen hjørne \(A\), tar vi utgangspunkt i dette hjørnet for å bestemme \(AC\) med cosinussetningen. Setningen forteller oss da at
Vi bruker CAS til å bestemme \(AC\):
Altså får vi at
Cosinussetningen er en slagkraftig setning som sammen med sinussetningen og arealsetningen lar oss finne ut svært mye om trekanter fra lite informasjon. Vi tar et sammensatt eksempel for å se hvordan vi kan bruke cosinussetningen i praksis.
Eksempel 1
Nedenfor vises en firkant \(\square ABCD\).
Bestem omkretsen \(\mathcal{O}\) til \(\square ABCD\).
Løsning
Omkretsen til \(\square ABCD\) er summen av lengdene til alle sidene:
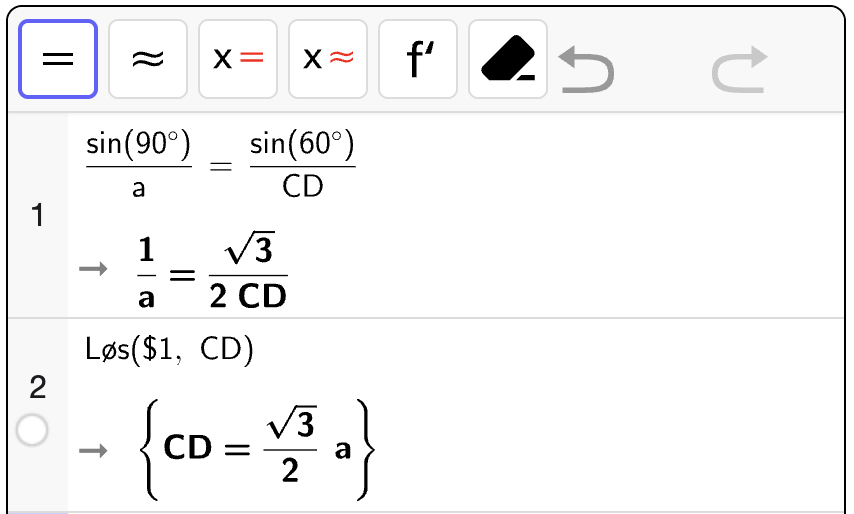
Vi mangler å bestemme \(AD\) som vi må kan gjøre i steg. Først bestemme vi diagonale \(BD\), deretter \(AD\). Begge disse lengene kan vi bestemme ved hjelp av cosinussetningen som følger.
Vi starter med å dele opp firkanten i to trekanter, \(\triangle ABD\) og \(\triangle BCD\). Vi lar diagonalen \(BD = x\). Da kan vi bruke cosinussetningen med utgangspunkt i hjørne \(C\) i \(\triangle BCD\) for å bestemme \(x\):
Vi bestemmer \(x\) med CAS:
Altså er \(x = BD = 4\sqrt{3}\).
Vi lar så \(y = AD\). Vi kan bruke cosinussetningen én gang til for å bestemme \(AD\) ved å ta utgangspunkt i hjørne \(A\) i \(\triangle ABD\):
Vi bestemmer \(y\) med CAS:
Dermed er \(y = AD = 4\). Omkretsen \(\mathcal{O}\) av \(\square ABCD\) er da:
Det kan nå være naturlig å stille seg spørsmål: hvordan vet vi at cosinussetningen stemmer? Vi skal nå snu oss mot dette problemet og se hvordan vi kan komme fram til setningen for en vilkårlig trekant.
Utforsk 1
Nedenfor vises en trekant \(\triangle ABC\) og en rettvinklet “hjelpetrekant” \(\triangle DAC\).
Til sammen utgjør de en rettvinklet trekant \(\triangle DBC\).
Bruk trigonometri til å uttrykke lengden \(y\) ved hjelp av lengden \(b\) og vinkelen \(u\).
Fasit
Løsning
Fra definisjonen av \(\sin u\) i \(\triangle DAC\) har vi at \(y\) er motstående katet til \(v\) og \(b\) er hypotenusen. Da følger det at
Bruk trigonometri til å uttrykke lengden \(x\) ved hjelp av lengden \(b\) og vinkelen \(u\).
Fasit
Løsning
Fra definisjonen av \(\cos u\) i \(\triangle DAC\) har vi at \(x\) er hosliggende katet til \(u\) og \(b\) er hypotenusen. Da følger det at
Bruk Pytagoras’ setning på trekant \(\triangle DBC\) til å finne beskrive sammenhengen mellom lengdene \(a\), \(b\), \(c\) og vinkelen \(u\).
Husk på Pytagoras’ identitet for cosinus og sinus: \((\sin u)^2 + (\cos u)^2 = 1\).
Fasit
Beskriv en sammenheng mellom \(\cos v\) og \(\cos u\). Bruk dette til å komme fram til cosinussetningen for \(\triangle ABC\) uttrykt ved hjelp av lengdene \(a\), \(b\), \(c\) og vinkelen \(v\).
Fasit
og