Oppgaver: Polynomfunksjoner

Oppgave 1

a

Grafen til en tredjegradsfunksjon \(f\) er vist i Fig. 16.5.

Bestem \(f(x)\).

Fig. 16.5 viser grafen til en tredjegradsfunksjon \(f\).

Fasit

\[ f(x) = \dfrac{1}{2}(x + 2)(x - 1)(x - 3) \]

b

Grafen til en tredjegradsfunksjon \(g\) er vist i Fig. 16.6.

Bestem \(g(x)\).

Fig. 16.6 viser grafen til en tredjegradsfunksjon \(g\).

Fasit

\[ g(x) = -\dfrac{1}{4}(x - 3)^2(x + 2) \]

c

Grafen til en tredjegradsfunksjon \(h\) er vist i Fig. 16.7.

Bestem \(h(x)\).

Fig. 16.7 viser grafen til en tredjegradsfunksjon \(h\).

Fasit

\[ h(x) = -\dfrac{1}{2}(x + 2)(x + 3)(x - 1) \]

d

Grafen til en tredjegradsfunksjon \(p\) er vist i Fig. 16.8.

Bestem \(p(x)\).

Fig. 16.8 viser grafen til en tredjegradsfunksjon \(p\).

Fasit

\[ p(x) = -(x + 2)^3 \]

---

Oppgave 2

Grafen til en tredjegradsfunksjon \(f\) gitt ved

\[ f(x) = ax^3 + bx^2 + cx + d, \]

er vist i

Fig. 16.9 viser grafen til en tredjegradsfunksjon \(f\).

a

Sett opp en likningssystem for koeffisientene uttrykt ved \(f(x)\).

Det vil si, én av likningene blir \(f(-3) = -2\) siden grafen går gjennom \((-3, -2)\).

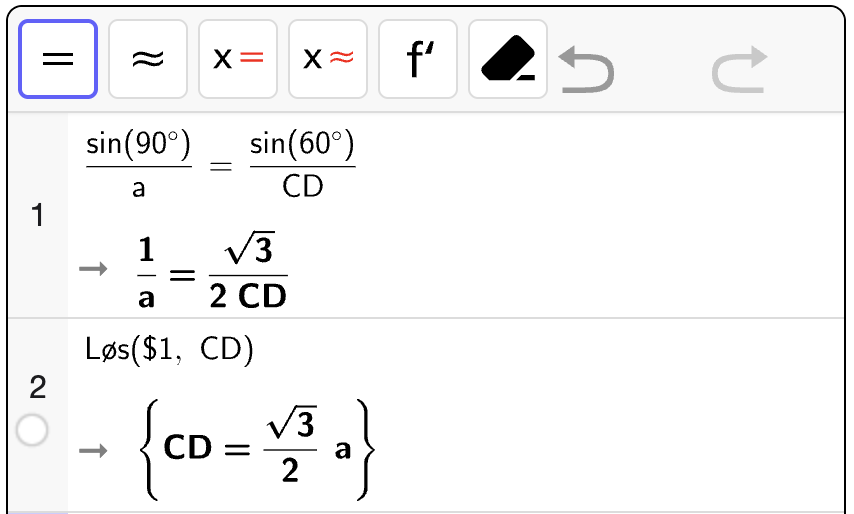
Fasit

\[ f(-3) = -2 \and f(-2) = 3 \and f(-1) = 2 \and f(0) = 1. \]

b

Her skal du bruke CAS til å bestemme koeffisientene til \(f(x)\).

Bestem \(f(x)\).

Åpne CAS‑vindu

Fasit

\[ f(x) = x^3 + 3x^2 + x + 1. \]

Løsning

Vi skriver inn et generelt funksjonsuttrykk og likningene i CAS, og løser deretter likningssystemet:

som betyr at

\[ a = 1 \and b = 3 \and c = 1 \and d = 1. \]

Dermed er

\[ f(x) = x^3 + 3x^2 + x + 1. \]

---

Oppgave 3

Bruk CAS til å bestemme funksjonsuttrykkene for hver av funksjonene nedenfor.

a

Grafen til en tredjegradsfunksjon \(f\) er vist i figuren nedenfor.

Bestem \(f(x)\).

Åpne CAS‑vindu

b

Grafen til en tredjegradsfunksjon \(g\) er vist i figuren nedenfor.

Bestem \(g(x)\).

Åpne CAS‑vindu

c

Grafen til en tredjegradsfunksjon \(h\) er vist i figuren nedenfor.

Bestem \(h(x)\).

Åpne CAS‑vindu

d

Grafen til en tredjegradsfunksjon \(p\) er vist i figuren nedenfor.

Bestem \(p(x)\).

Åpne CAS‑vindu

---

Oppgave 4

En tredjegradsfunksjon \(f\) er gitt ved

\[ f(x) = -(x + 1)(x - 1)(x - 2). \]

a

Bestem nullpunktene til \(f\).

Fasit

\[ f(x) = 0 \liff x = -1 \or x = 1 \or x = 2. \]

b

Tegn en fortegnslinje for \(f(x)\) inkludert faktorene til \(f\).

Fasit

c

Lag en skisse av grafen til \(f\).

Fasit

d

Løs ulikheten

\[ f(x) > 0. \]

Fasit

\[ x \in \langle \gets, -1 \rangle \cup \langle 1, 2 \rangle. \]

---

Oppgave 5

En tredjegradsfunksjon \(f\) er gitt ved

\[ f(x) = (x - 1)^2 (x + 3) \]

a

Bestem nullpunktene til \(f\).

Fasit

\[ f(x) = 0 \liff x = 1 \or x = -3. \]

b

Tegn et fortegnsskjema for \(f(x)\).

Fasit

c

Tegn en skisse av grafen til \(f\).

Fasit

d

Løs ulikheten

\[ f(x) > 0. \]

Fasit

Det holder med ett av alternativene under.

\[ x \in \langle -3, \to \rangle \setminus \{1\} \liff x > -3 \and x \neq 1. \]

---

Oppgave 6

En fjerdegradsfunksjon \(f\) er gitt ved

\[ f(x) = (x + 1)^2(x - 2)(x - 3). \]

a

Bestem nullpunktene til \(f\).

Fasit

\[ f(x) = 0 \liff x = -1 \or x = 2 \or x = 3. \]

b

Tegn et fortegnsskjema for \(f(x)\), inkludert faktorene i \(f(x)\).

Fasit

c

Tegn en skisse av grafen til \(f\).

Fasit

d

Løs ulikheten

\[ f(x) \leq 0. \]

Fasit

Det holder med ett av alternativene under.

\[ x \in [2, 3] \cup \{-1\} \liff -2 \leq x \leq 3 \or x = -1. \]