Oppgaver: \sin v, \cos v og \tan v

Oppgaver: \(\sin v\), \(\cos v\) og \(\tan v\)#

Oppgave 1

I figuren nedenfor vises en rettvinklet trekant.

a

Bestem \(\sin B\) og \(\cos B\).

Fasit

\[ \sin B = \dfrac{6}{10} = \dfrac{3}{5} \quad \quad \quad \cos B = \dfrac{8}{10} = \dfrac{4}{5} \]

b

Bestem \(\tan B\).

Fasit

\[ \tan B = \dfrac{6}{8} = \dfrac{3}{4} \]

c

Bestem \(\sin C\) og \(\cos C\).

Fasit

\[ \sin C = \dfrac{8}{10} = \dfrac{4}{5} \quad \quad \quad \cos C = \dfrac{6}{10} = \dfrac{3}{5} \]

d

Bestem \(\tan C\).

Fasit

\[ \tan C = \dfrac{8}{6} = \dfrac{4}{3} \]

Oppgave 2

I figuren nedenfor vises en rettvinklet trekant.

a

Bestem \(BC\).

Fasit

\[ BC = \sqrt{3}. \]

b

Bestem \(\sin A\) og \(\cos A\).

Fasit

\[ \sin A = \dfrac{1}{2} \quad \quad \quad \cos A = \dfrac{\sqrt{3}}{2} \]

c

Bestem \(\tan A\).

Fasit

\[ \tan A = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3} \]

d

Bestem \(\sin C\) og \(\cos C\).

Fasit

\[ \sin C = \dfrac{\sqrt{3}}{2} \quad \quad \quad \cos C = \dfrac{1}{2} \]

e

Bestem \(\tan C\).

Fasit

\[ \tan C = \sqrt{3} \]

Oppgave 3

I denne oppgaven skal du bruke CAS til å bestemme vinklene i trekanten.

I figuren nedenfor vises den samme rettvinklete trekanten du jobbet med i oppgave 2.

For å skrive \(A^\circ\) i CAS-vinduet, kan du bruke “Alt” + “o” på Windows og “⌥” (option) + “o” på Mac for å få gradertegnet \(^\circ\)

a

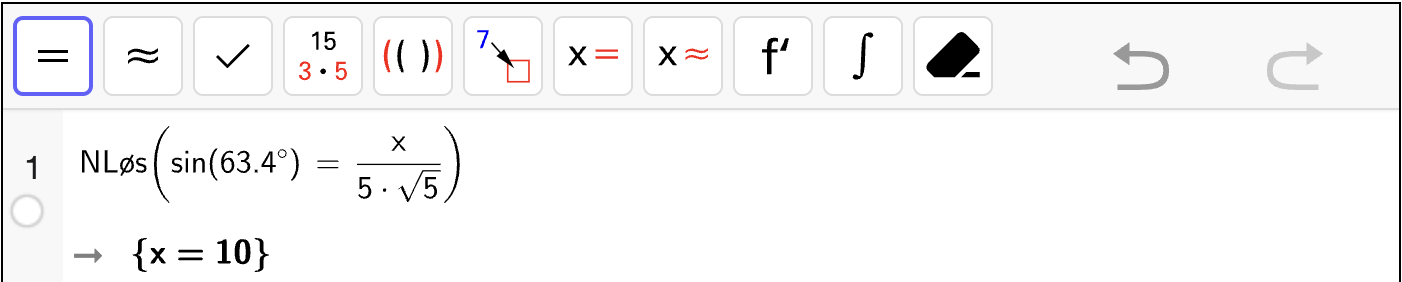
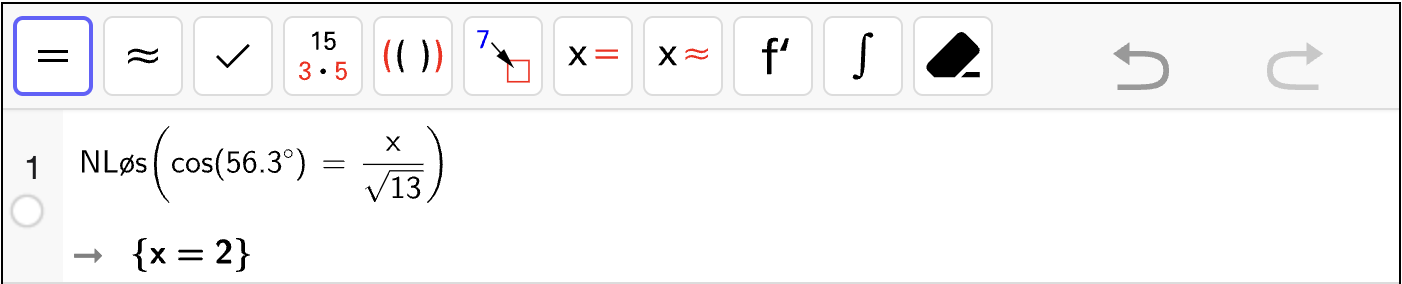
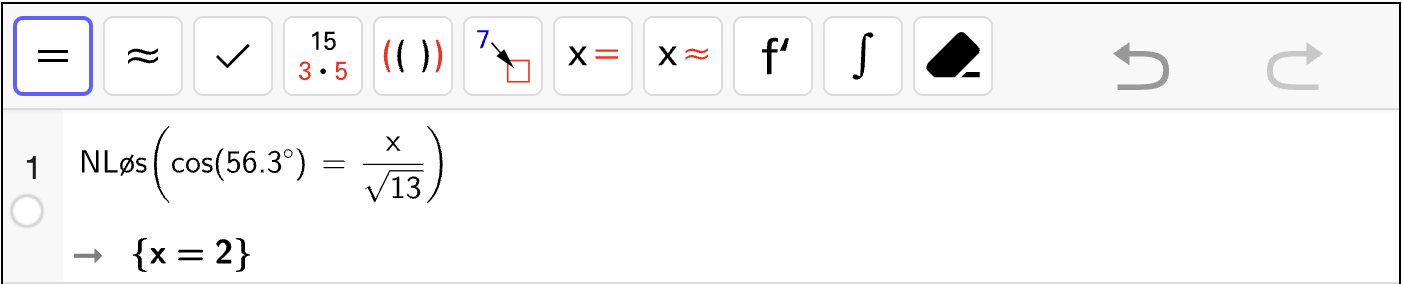
Bestem vinkel \(A\) ved å løse en passende likning med \(\sin A^\circ\).

Fasit

Dermed er \(A = 30\).

b

Bestem vinkel \(C\) ved å løse en passende likning med \(\sin C^\circ\).

For å skrive kvadratrot \(\sqrt{x}\) i CAS-vinduet, kan du bruke sqrt(x)-funksjonen.

Fasit

Dermed er \(C = 60\). Dette er den eneste løsningen som som tilfredsstiller \(C^\circ \in [0^\circ, 90^\circ]\).

c

Bestem vinkel \(C\) ved å løse en passende likning med \(\cos C^\circ\).

Fasit

Dermed er \(C = 60\).

CAS-vindu

Oppgave 4

I denne oppgaven skal du bruke CAS til å regne ut \(\sin v\), \(\cos v\) og \(\tan v\) for ulike vinkler \(v\).

a

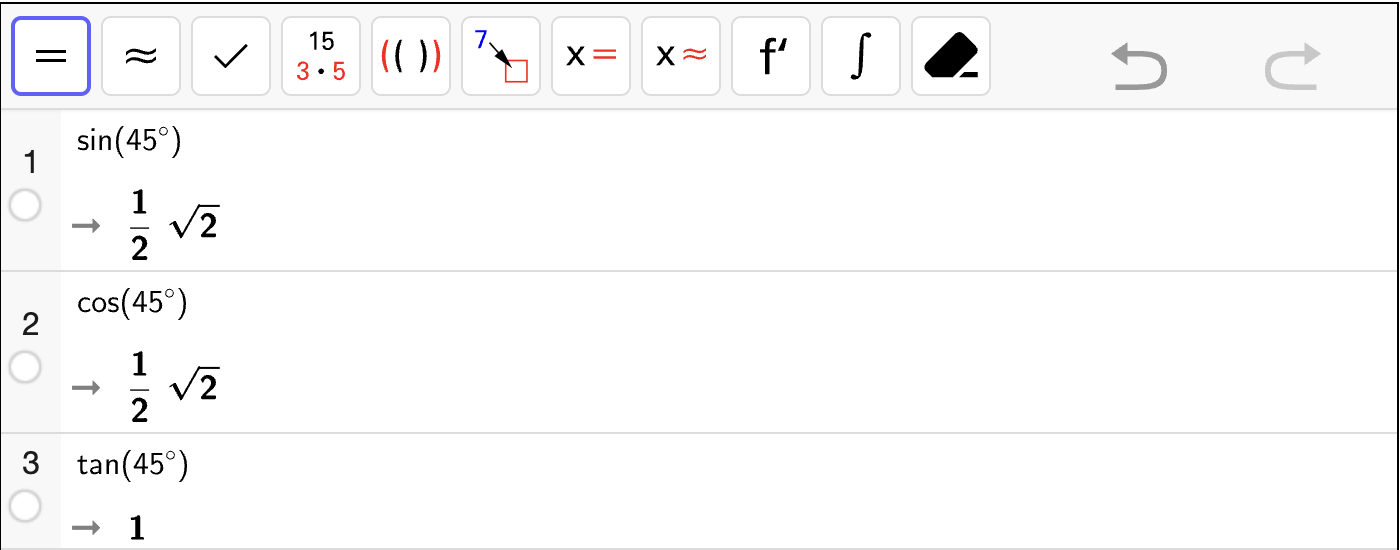
Bruk CAS til å regne ut \(\sin 45^\circ\), \(\cos 45^\circ\) og \(\tan 45^\circ\).

Fasit

Altså er

\[ \sin 45^\circ = \frac{\sqrt{2}}{2} \quad \quad \quad \cos 45^\circ = \frac{\sqrt{2}}{2} \quad \quad \quad \tan 45^\circ = 1 \]

b

Bruk CAS til å regne ut \(\sin 60^\circ\), \(\cos 60^\circ\) og \(\tan 60^\circ\).

Fasit

Altså er

\[ \sin 60^\circ = \frac{\sqrt{3}}{2} \quad \quad \quad \cos 60^\circ = \frac{1}{2} \quad \quad \quad \tan 60^\circ = \sqrt{3} \]

CAS-vindu

Oppgave 5

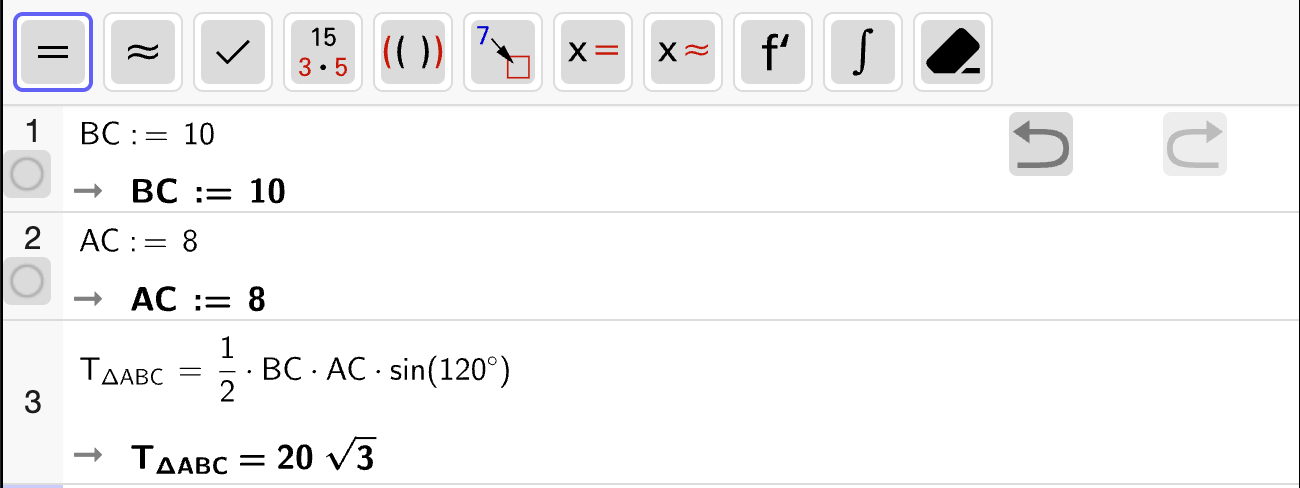
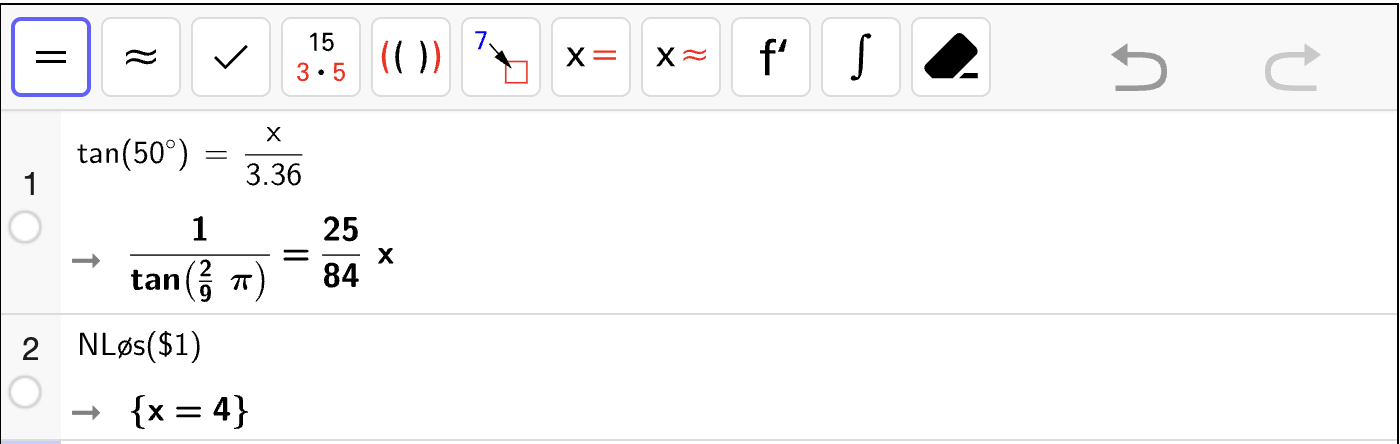
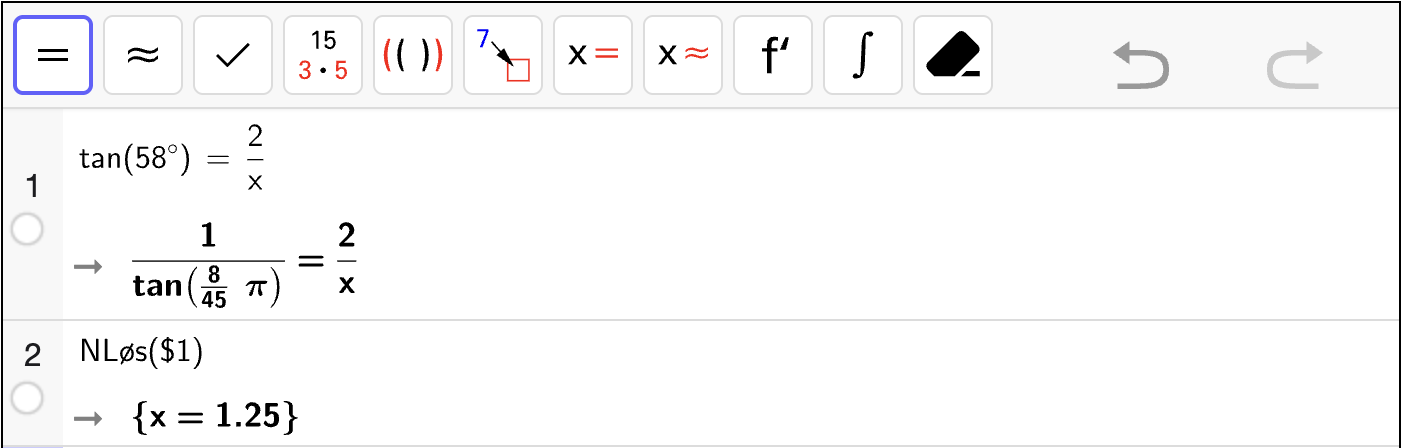
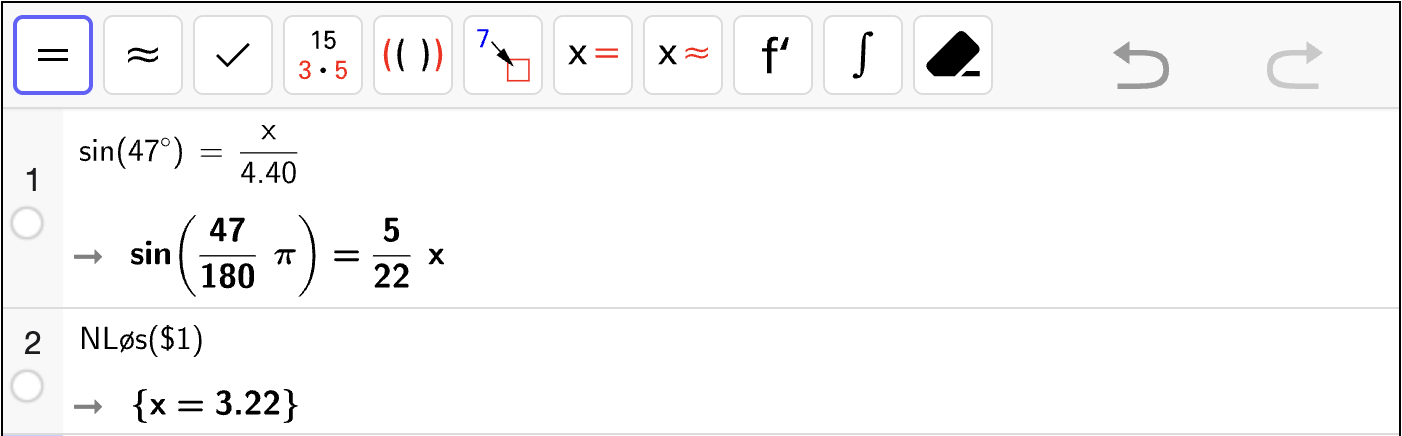
I denne oppgaven skal du bruke CAS til å bestemme ukjente sidelenger i rettvinklede trekanter.

a

I figuren nedenfor vises en rettvinklet trekant.

Bruk CAS til å bestemme \(x\).

Fasit

Dermed er \(x = 10\).

b

I figuren nedenfor vises en rettvinklet trekant.

Bruk CAS til å bestemme \(x\).

Fasit

Dermed er \(x = 2\).

c

I figuren nedenfor vises en rettvinklet trekant.

Bruk CAS til å bestemme \(x\).

Fasit

Dermed er \(x = 4\sqrt{2}\).

d

I figuren nedenfor vises en rettvinklet trekant.

Bruk CAS til å bestemme \(x\).

Fasit

Altså er \(x = 4\).

e

I figuren nedenfor vises en rettvinklet trekant.

Bruk CAS til å bestemme \(x\).

Fasit

Altså er \(x = 1.25\).

f

I figuren nedenfor vises en rettvinklet trekant.

Bruk CAS til å bestemme \(x\).

Fasit

Altså er \(x = 3.22\).

Oppgave 6

En likesidet trekant er vist i figuren nedenfor.

a

Bestem høyden \(h\) i trekanten.

Fasit

\[ h = \sqrt{3}. \]

b

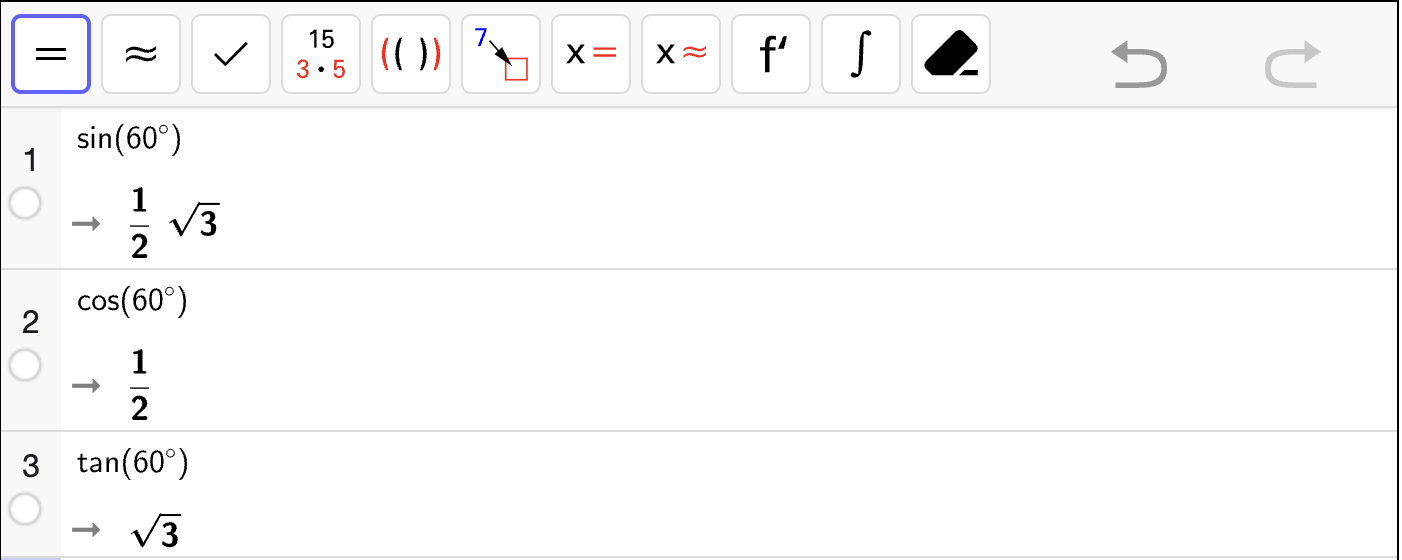
Bruk trekanten til å bestemme en eksakt verdi for \(\sin 60^\circ\) og \(\cos 60^\circ\).

Fasit

\[ \sin 60^\circ = \frac{\sqrt{3}}{2} \quad \quad \quad \cos 60^\circ = \frac{1}{2} \]

c

Bruk trekanten til å bestemme en eksakt verdi for \(\sin 30^\circ\) og \(\cos 30^\circ\).

Fasit

\[ \sin 30^\circ = \frac{1}{2} \quad \quad \quad \cos 30^\circ = \frac{\sqrt{3}}{2} \]

d

Vis at

\[ (\cos v)^2 + (\sin v)^2 = 1 \]

for \(v = 30^\circ\) og \(v = 60^\circ\).

Oppgave 7

Bruk trekanten nedenfor til å bestemme en eksakt verdi for \(\sin 45^\circ\) og \(\cos 45^\circ\).

Fasit

\[ \sin 45^\circ = \frac{\sqrt{2}}{2} \quad \quad \quad \cos 45^\circ = \frac{\sqrt{2}}{2} \]

Oppgave 8

I en matematikkbok står det følgende:

Setning

For en vinkel \(v\), gjelder

\[ 2 \sin (v) \cdot \cos (v) = \sin (2\cdot v) \]

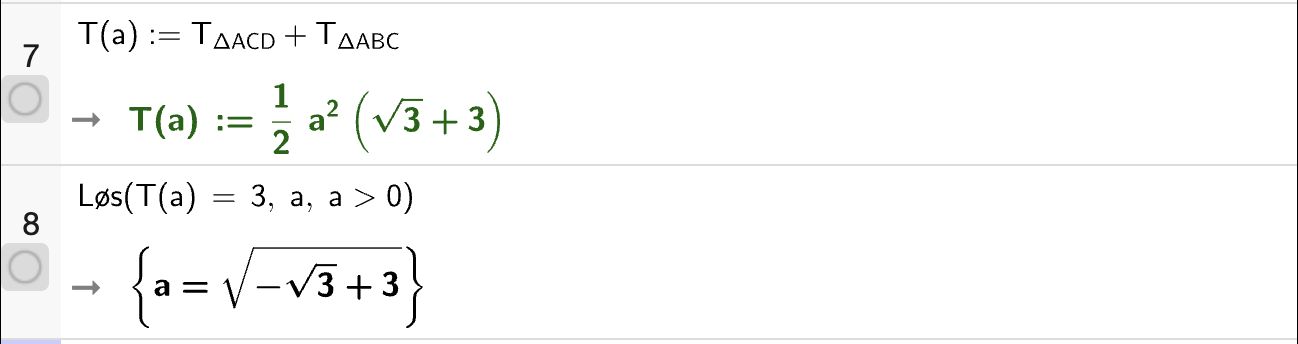
Vis at formelen stemmer for trekanten nedenfor med \(v = 30^\circ\).

Oppgave 9

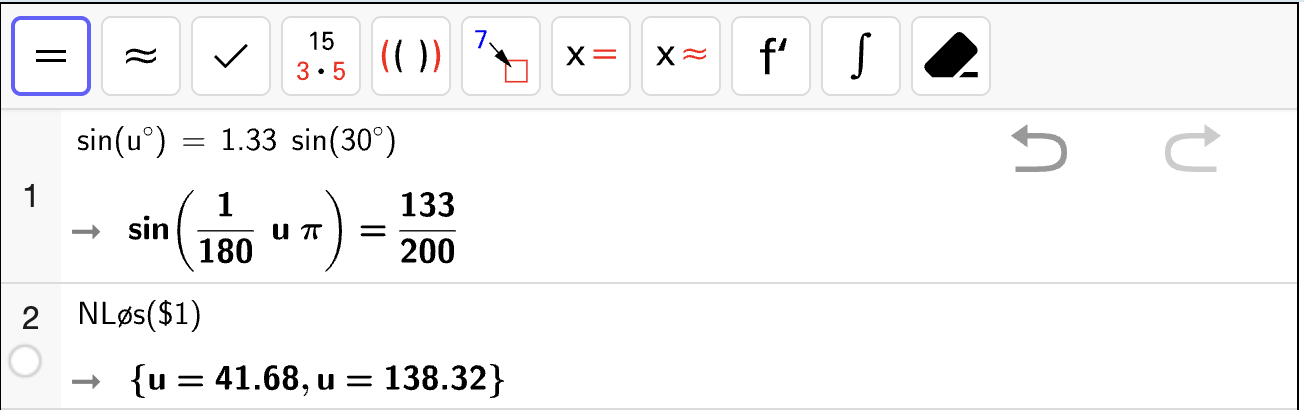
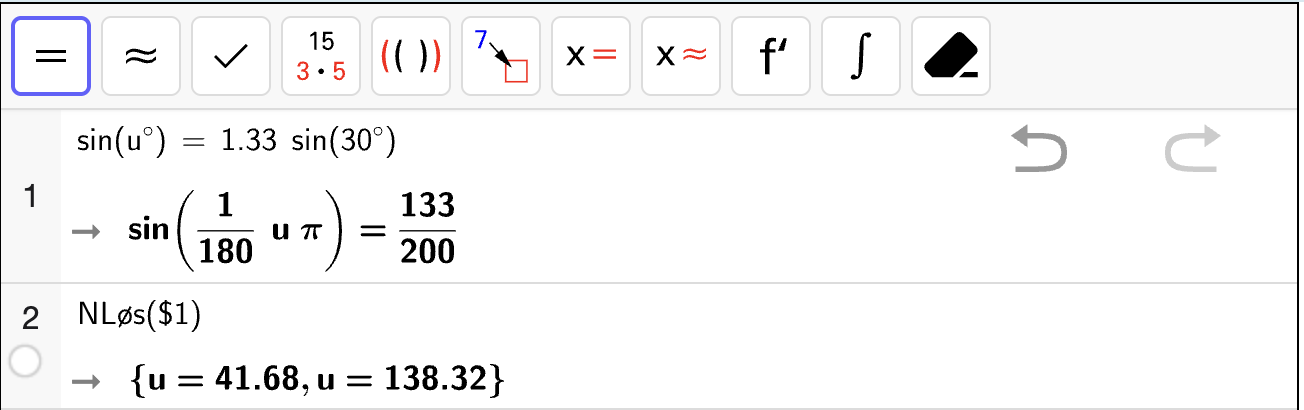
Snells lov forteller oss at når lys går fra luft til vann, vil lyset brytes slik at lysstrålen sin retning i luft og vann oppfyller

\[ \sin u = 1.33 \cdot \sin v \]

a

Hvor stor vinkel \(u\) må lyset ha for at vinkelen etter brytning i vannet skal være \(v = 30^\circ\)?

Fasit

\(u \approx 41.68 \degree\).

b

Hva blir retningen til lysstrålen i vannet når \(u\) nærmer seg \(0^\circ\). Gi en praktisk tolkning av svaret.

Fasit

Når \(u \approx 0^\circ\), vil \(\sin u \approx 0\) og dermed \(\sin v \approx 0\). Dermed vil lysstrålen gå parallelt med innfallsloddet og vannstrålen endrer ikke retning når den går gjennom vannoverflaten. Det skjer altså ingen brytning.

Oppgave 10

En lysstråle har beveget seg fra et punkt \(A(0, 1)\) i luft til et punkt \(B(10, -1)\) i vann. Lyset traff vannoverflaten i et punkt \(M(x, 0)\). Alle avstander er i kilometer.

I figuren nedenfor vises en mulig bane for lysstrålen.

a

Lag en modell \(L_\text{luft}\) som beskriver hvor mange kilometer \(L_\text{luft}(x)\) lysstrålen har beveget seg i luft før den traff vannoverflaten i punktet \(M(x, 0)\).

Fasit

\[ L_\text{luft}(x) = \sqrt{x^2 + 1} \]

b

Lag en modell \(L_\text{vann}\) som beskriver hvor mange kilometer \(L_\text{vann}(x)\) lysstrålen har beveget seg i vann etter at den traff vannoverflaten i punktet \(M(x, 0)\) og endte opp i \(B(10, -1)\).

Fasit

\[ L_\text{vann}(x) = \sqrt{(10 - x)^2 + 1} \]

c

Lys beveger seg med en fart på ca. 300 000 km/s i luft og ca. 225 000 km/s i vann.

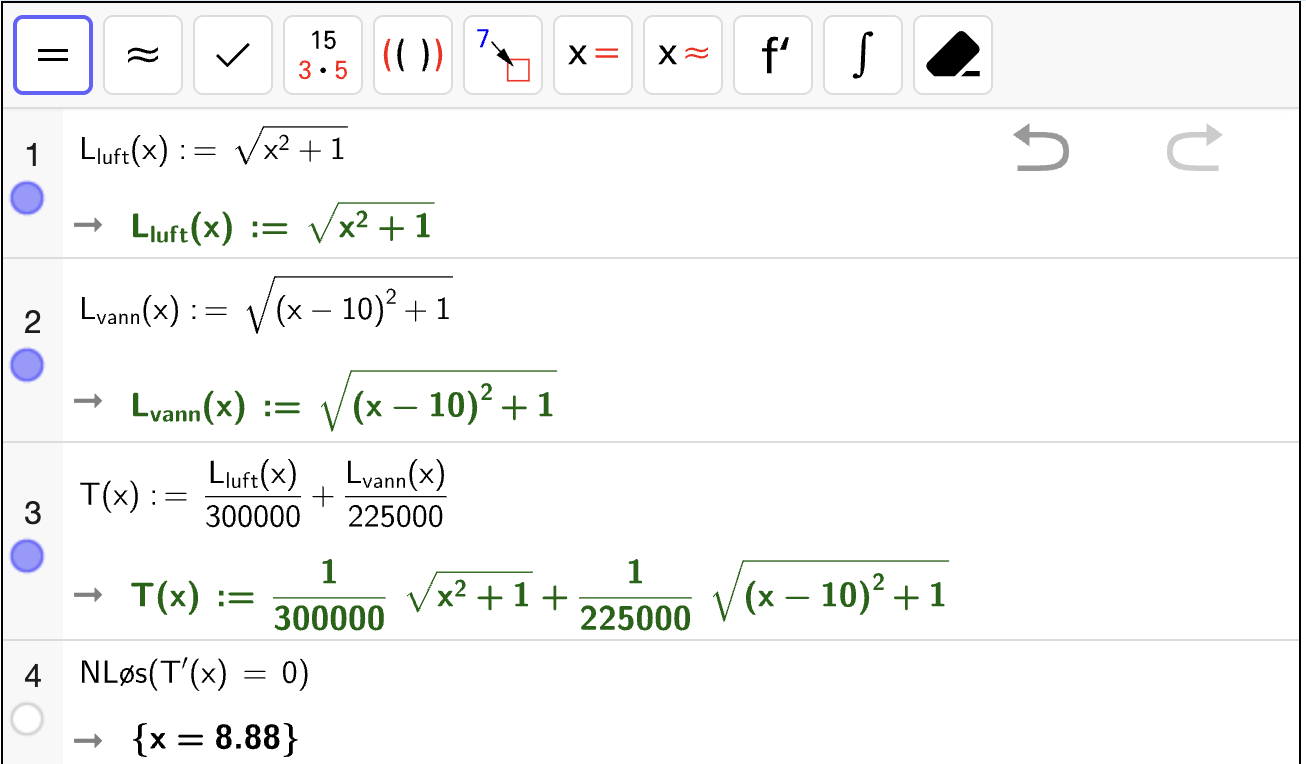
Lag en modell \(T\) som beskriver hvor mange sekunder \(T(x)\) det tar for lysstrålen å bevege seg fra \(A\) til \(B\) via punktet \(M(x, 0)\).

Hint: Vei-fart-tid

For en strekning \(L\), en fart \(v\) og en tid \(t\), gjelder

\[ L = v \cdot t. \]

Fasit

\[ T(x) = \dfrac{L_\text{luft}(x)}{300000} + \dfrac{L_\text{vann}(x)}{225000} \]

d

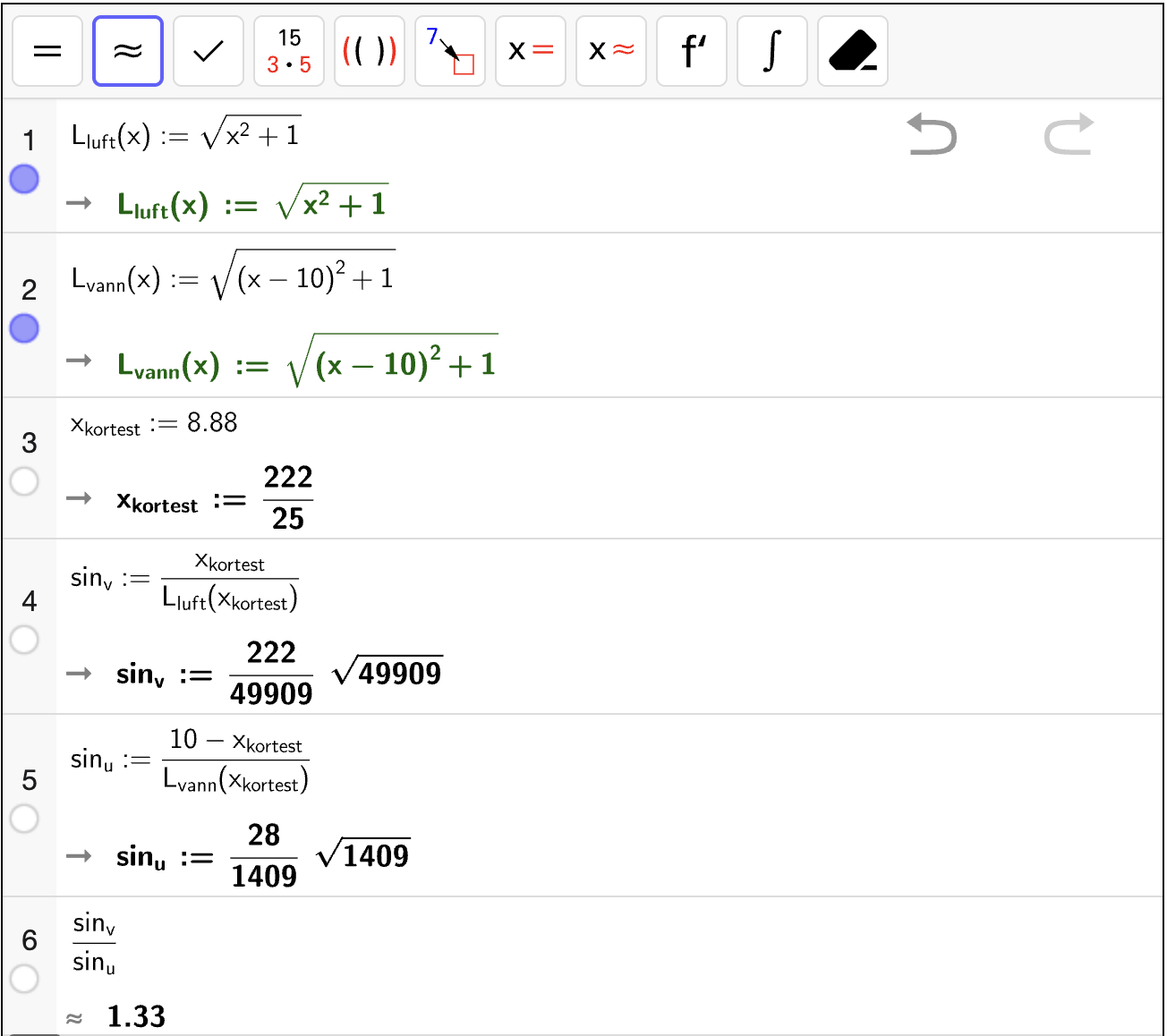
Bestem i hvilket punkt \(M(x, 0)\) lysstrålen må ha truffet dersom lysstrålen skal bruke kortest mulig tid mellom \(A\) og \(B\).

Fasit

Altså gikk vannstrålen gjennom \(M(8.88, 0)\) hvis den skulle bruke kortest mulig tid fra \(A\) til \(B\).

e

Bruk svaret ditt fra d til å vise at

\[ \dfrac{\sin u}{\sin v} = 1.33 \]

Fasit

Oppgave 11

a

Månen har en radius på ca. 1737 km og er ca. 384 400 km unna jorden.

Bestem hvor stor vinkel \(v\) månen dekker på himmelen sett fra jorden.

Fasit

\[ v = 0.5 \degree \]

b

Andromedagalaksen er vår nærmeste nabogalakse. Den er er ca. 200 000 lysår i diameter og 2.5 millioner lysår unna oss.

Bestem hvor stor vinkel \(v\) Andromeda dekker på himmelen sett fra jorden.

Dekker månen eller Andromedagalaksen størst vinkel på himmelen?

Fasit

\[ v = 4.58 \degree. \]

Oppgave 12

Nedenfor vises en rettvinklet trekant med vinkler \(u\) og \(v\).

Avgjør om påstandene nedenfor stemmer eller ikke.

a

For en rettvinklet trekant, gjelder alltid

\[ \sin v = \cos u \]

Fasit

Påstanden stemmer.

b

For en rettvinklet trekant, gjelder alltid

\[ \tan u \cdot \tan v = 1 \]

Fasit

Påstanden stemmer.

c

For en rettvinklet trekant, gjelder alltid

\[ (\cos v)^2 + (\sin v)^2 = 1 \]

Fasit

Påstanden stemmer.