CAS-kurs: Del 1

Læringsmål

• Kunne løse lineære likninger med CAS.

• Kunne løse lineære likningssystemer med CAS.

• Kunne løse lineære ulikheter med CAS.

CAS er en forkortelse for Computer Algebra System. CAS består av en samling funksjoner som er utviklet for å løse matematiske problemer symbolsk (algebraisk) på datamaskin på liknende vis som vi gjør når vi regner for hånd. Kan et problem løses for hånd, kan det også løses med CAS. Men CAS kan også løse problemer som ikke kan lar seg løses for hånd også!

Likninger

For å løse likninger med CAS, skriver vi inn likningen først – deretter bruker vi én av to innebygde funksjoner:

1. Vi bruker for å løse likningen eksakt. Eksakt løsning vil si at vi får et svar som er det nøyaktige svaret. Svaret kan blant annet inneholde kvadratrøtter eller brøker.

2. Vi bruker for å løse likningen numerisk. Numerisk løsning vil så si at vi får et tall som svar som ikke nødvendigvis er det nøyaktige svaret, men et omtrentlig svar. Svaret er ofte et desimaltall.

Eksakt løsning

For å skrive gangetegn i CAS-vinduet, bruker vi * mellom tall og variabler.

Utforsk 1

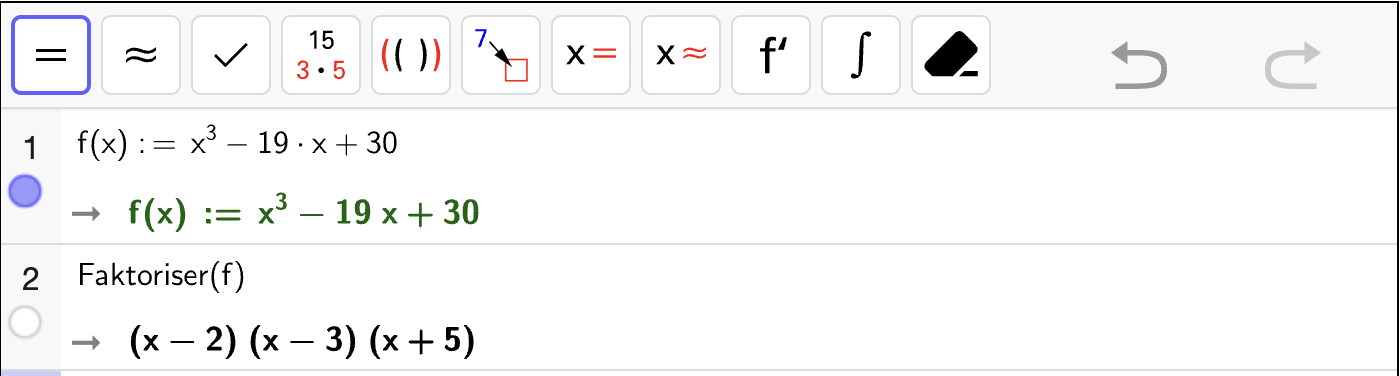
I Fig. 1 nedenfor vises det hvordan man kan løse en likning eksakt med i CAS.

Fig. 1 viser hvordan vi løser en likning eksakt med CAS. Vi skriver inn likningen og trykker på for å løse den.

Åpne CAS‑vindu

a

Hvilken likning er det som er løst i Fig. 1?

Fasit

\[ 2x - 6 = 0 \]

b

Bruk CAS til å løse likningen som er vist i Fig. 1 med å følge fremgangsmåten som er vist i figuren.

Fasit

Løsningen av likningen er derfor

\[ x = 3 \]

---

Numerisk løsning

I tilfeller hvor vi regner på noe praktisk kan det være naturlig å bruke numerisk løsning med . I disse tilfellene vil det gjerne være beregninger der vi er ute at et omtrentlig tallsvar som vi kunne målt i praksis. Andre ganger finnes det ikke en eksakt løsning i det hele tatt, men det går likevel an å finne en numerisk løsning.

Utforsk 2

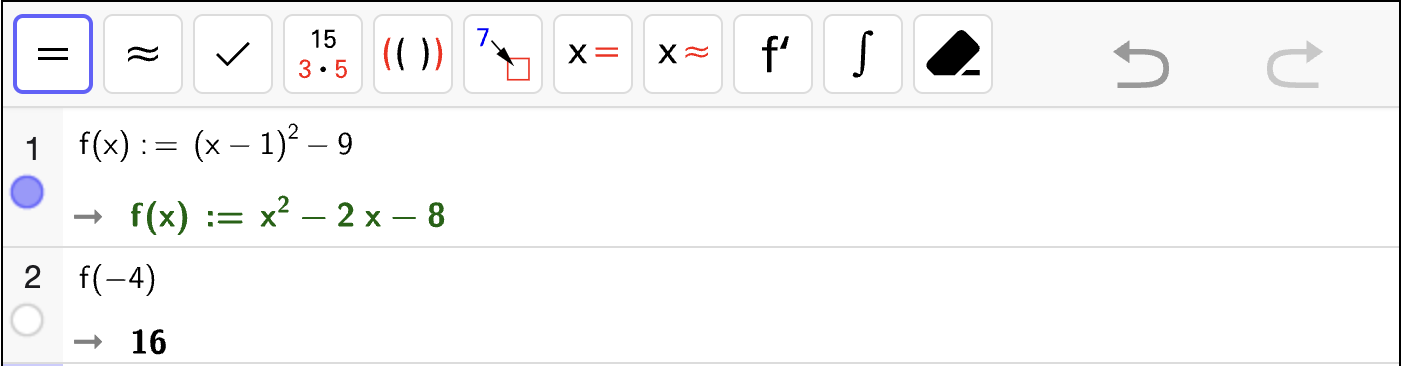
Nedenfor vises et CAS-vindu som løser en likning eksakt med og numerisk med .

a

1. Hvilken likning er det som er løst i CAS-vinduet?

2. Hva er den eksakte løsningen?

3. Hva er den numeriske løsningen?

b

Bruk CAS-vinduet til å løse likningen

\[ x^2 - 3x + 1 = 0 \]

1. Eksakt med

2. Numerisk med

Løsning

---

Ulikheter

For å løse ulikheter med CAS, bruker vi akkurat de samme funksjonene som vi bruker for å løse likninger. Forskjellen ligger i at vi må bruke ulikhetstegn i stedet for likhetstegn når vi skriver inn ulikhetene.

Eksakt løsning

Utforsk 3

I Fig. 2 nedenfor viser vi hvordan vi løser en ulikhet eksakt med CAS. Fremgangsmåten er lik den for likninger hvor vi:

1. Skriver inn ulikheten

2. Trykket på for å løse den.

Fig. 2 viser hvordan vi løser en ulikhet eksakt med CAS. Vi skriver inn ulikheter og så trykker vi på for å løse dem.

Åpne CAS‑vindu

a

Bruk CAS-vinduet til å løse ulikheten som løses i Fig. 2.

b

Bruk CAS-vinduet til å løse ulikheten

\[ -2x + 5 < 0 \]

---

Numerisk løsning

Når vi løste likninger, kunne vi løse dem numerisk med . Det kan vi ikke gjøre med ulikheter. Ønsker vi å finne en numerisk løsning av en ulikhet, må vi i stedet

1. Løse ulikheten eksakt med

2. Bruk til å finne en numerisk verdi for løsningen fra punkt 1.

I Utforsk 4 ser vi på hvordan.

Utforsk 4

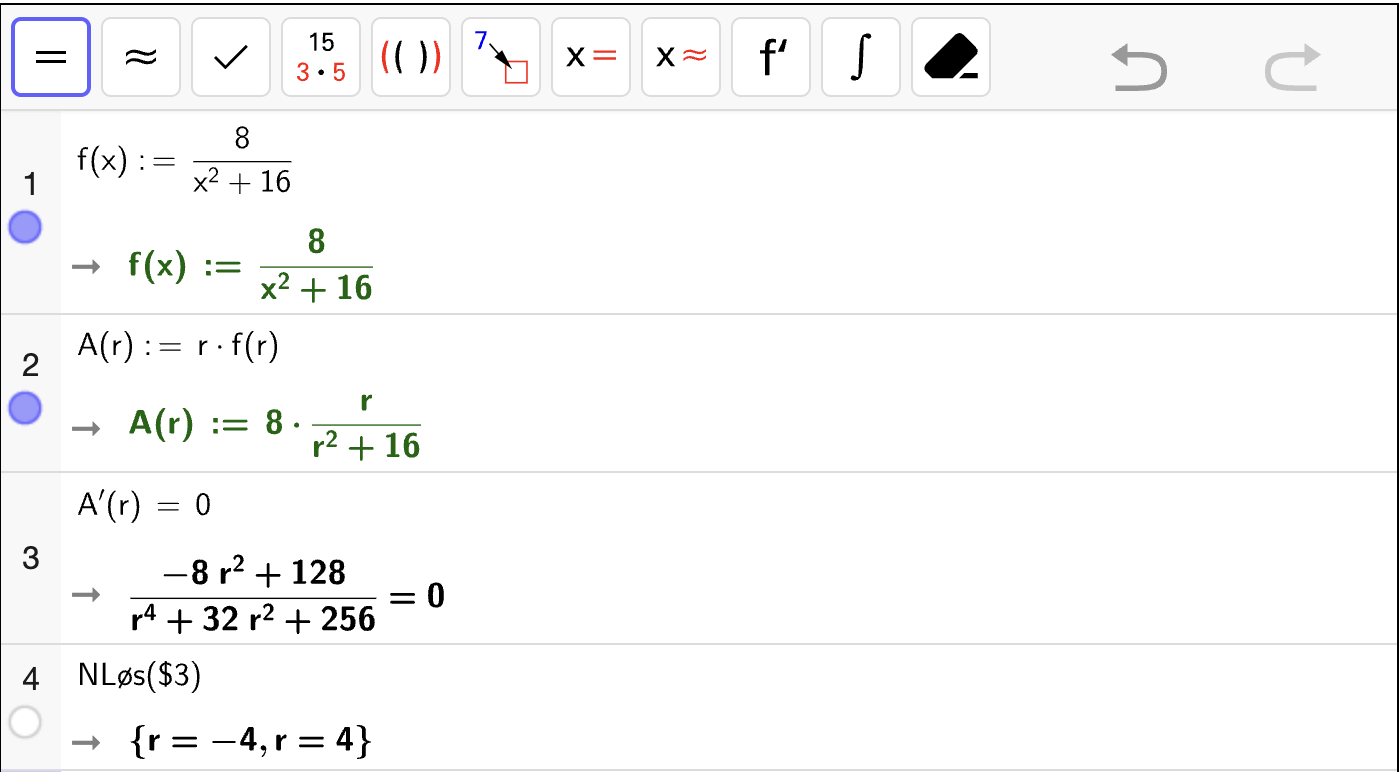
I Fig. 3 nedenfor viser vi hvordan man kan finne en numerisk løsning av en ulikhet med CAS. Det gjøres med følgende fremgangsmåte:

1. Løs ulikheten eksakt med

2. Bruk for å finne en numerisk verdi for løsningen fra punkt 1.

Fig. 3 viser hvordan man løser en ulikhet numerisk med CAS. Først løser vi den eksakt med og deretter bruker vi for å finne en numerisk verdi for løsningen.

Åpne CAS‑vindu

a

Løs ulikheten i Fig. 3 eksakt og numerisk på tilsvarende måte i CAS-vinduet.

b

Løs ulikheten nedenfor eksakt og numerisk på tilsvarende måte i CAS-vinduet.

\[ 3x + 2 < 0 \]

---

Likningssystemer

Likningssystemer kan vi løse både eksakt med og numerisk med . I Utforsk 5 ser vi på hvordan vi kan gjøre dette.

Utforsk 5

I figuren nedenfor vises det hvordan vi løser et likningssystem med CAS.

1. Først markerer vi likningene i likningssystemet.

2. Så løser vi likningssystemet eksakt med eller numerisk med .

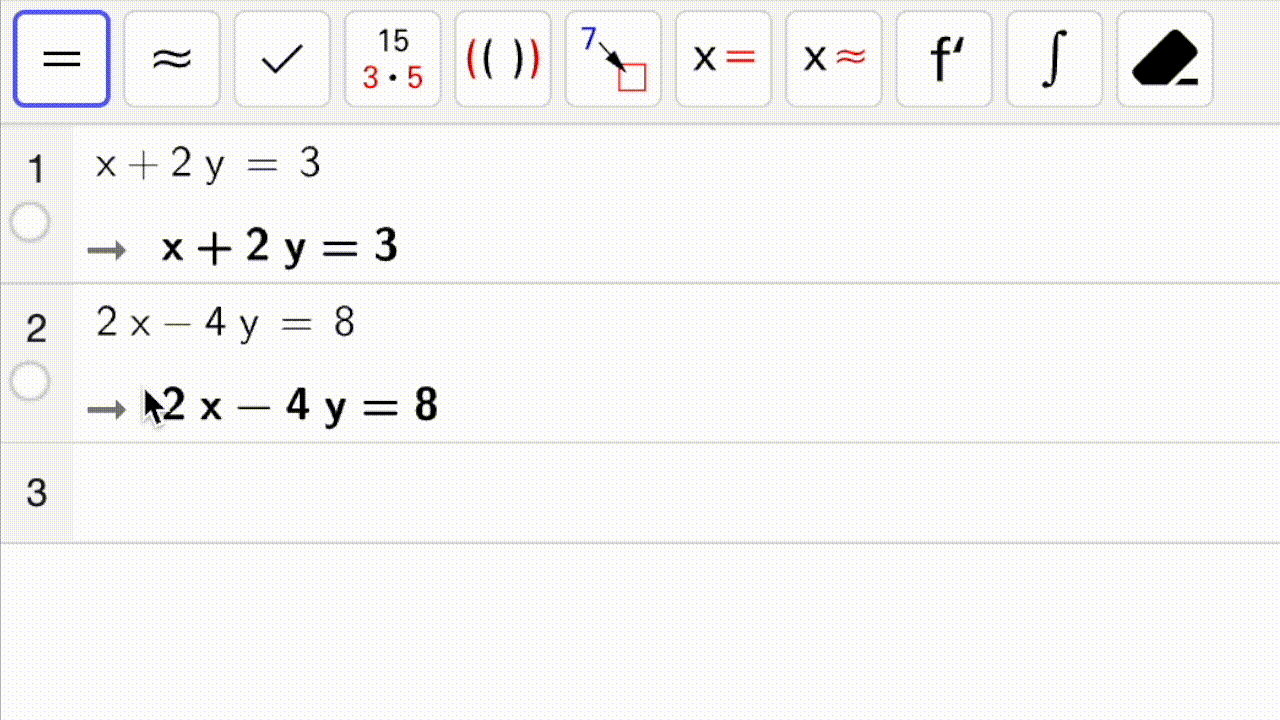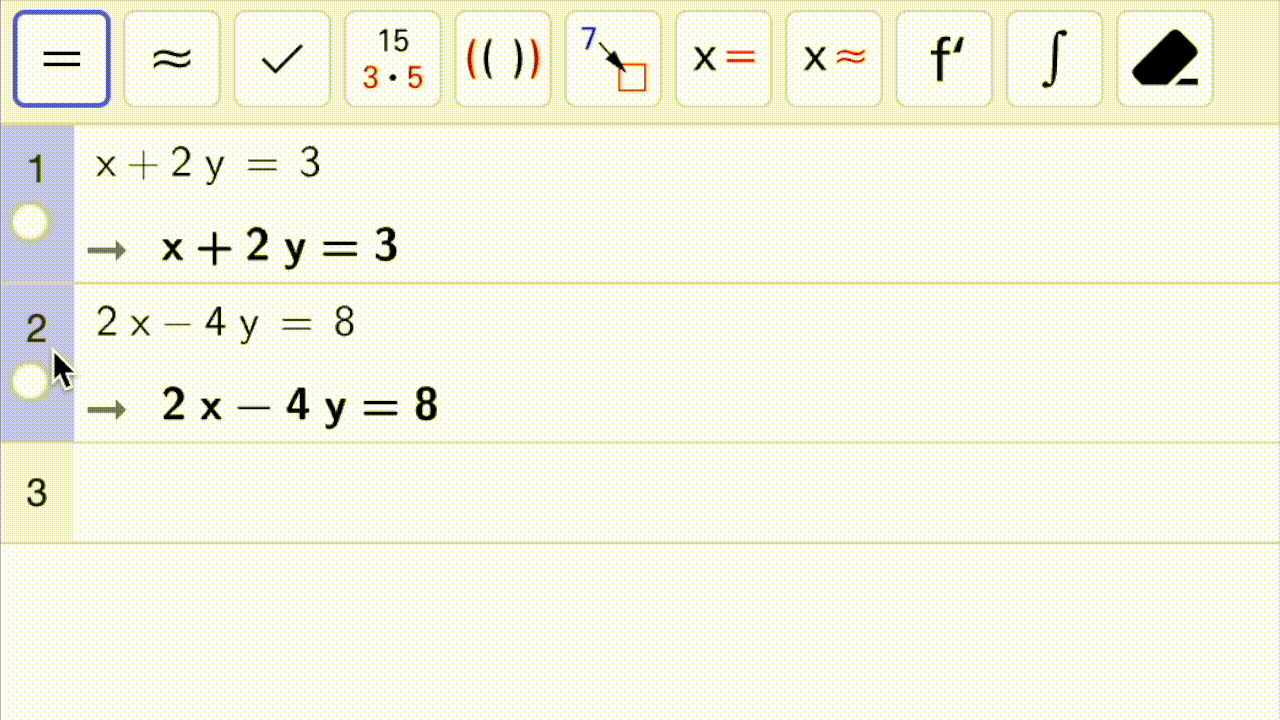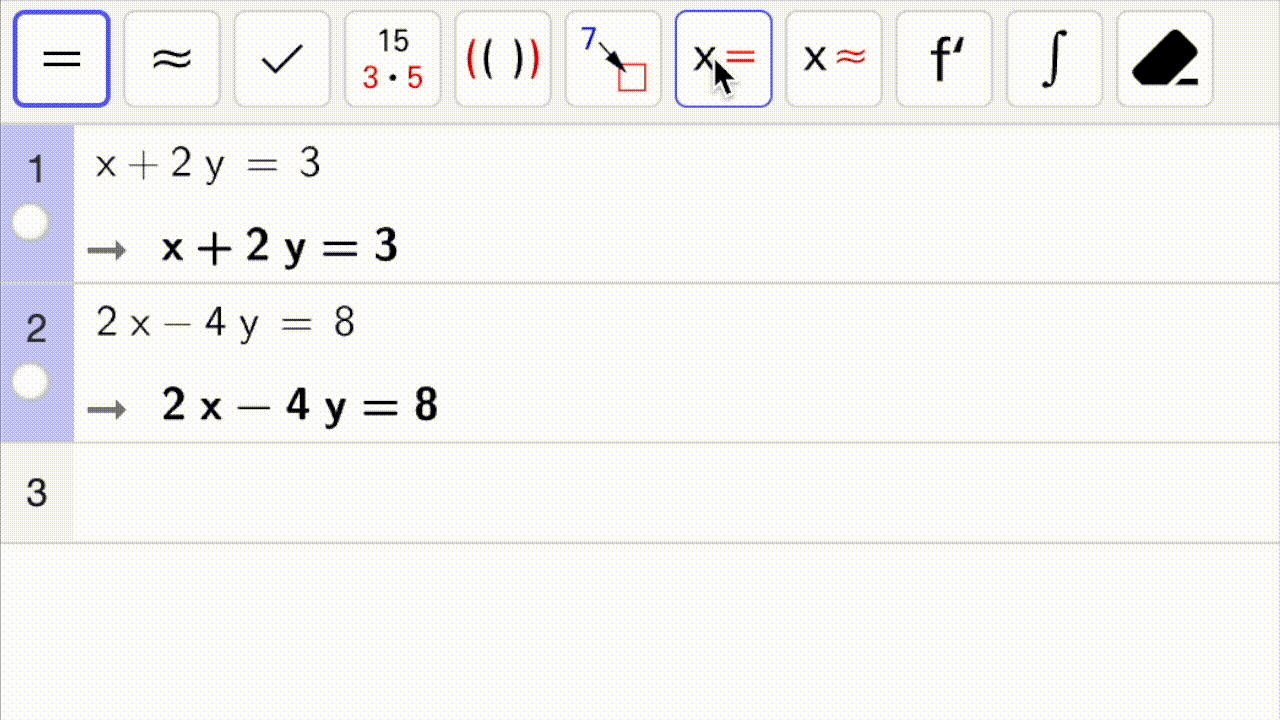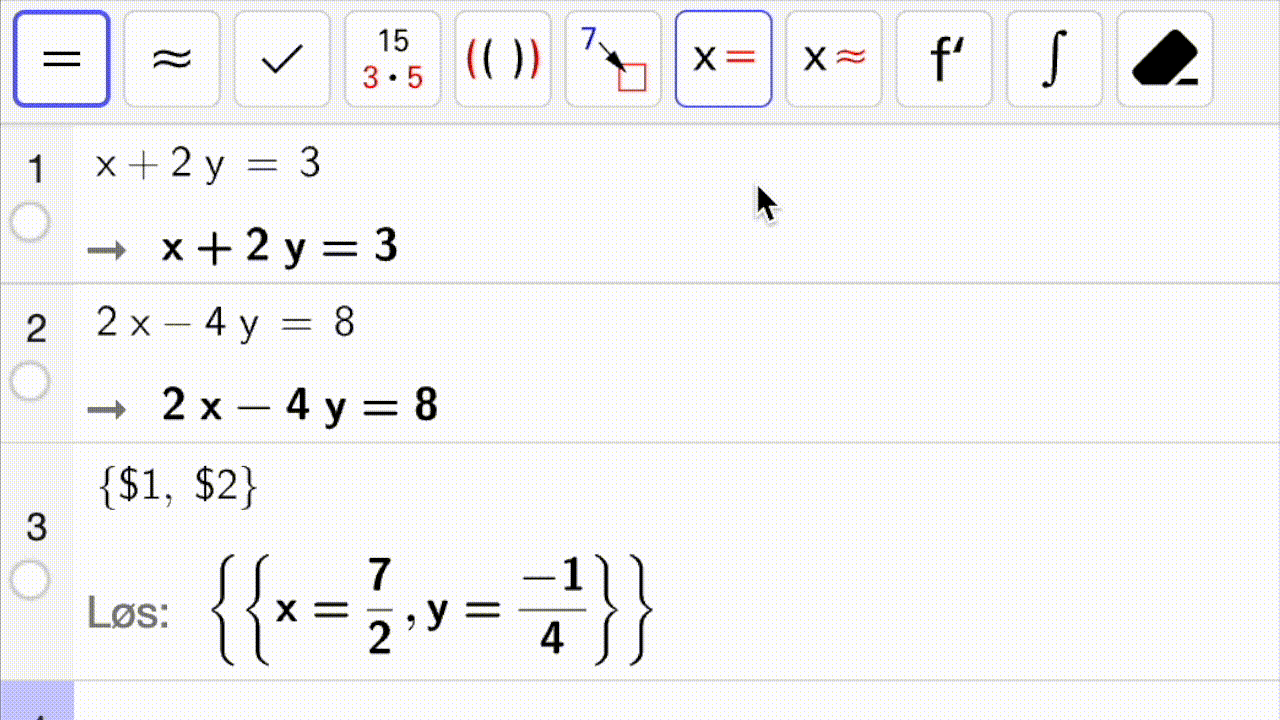
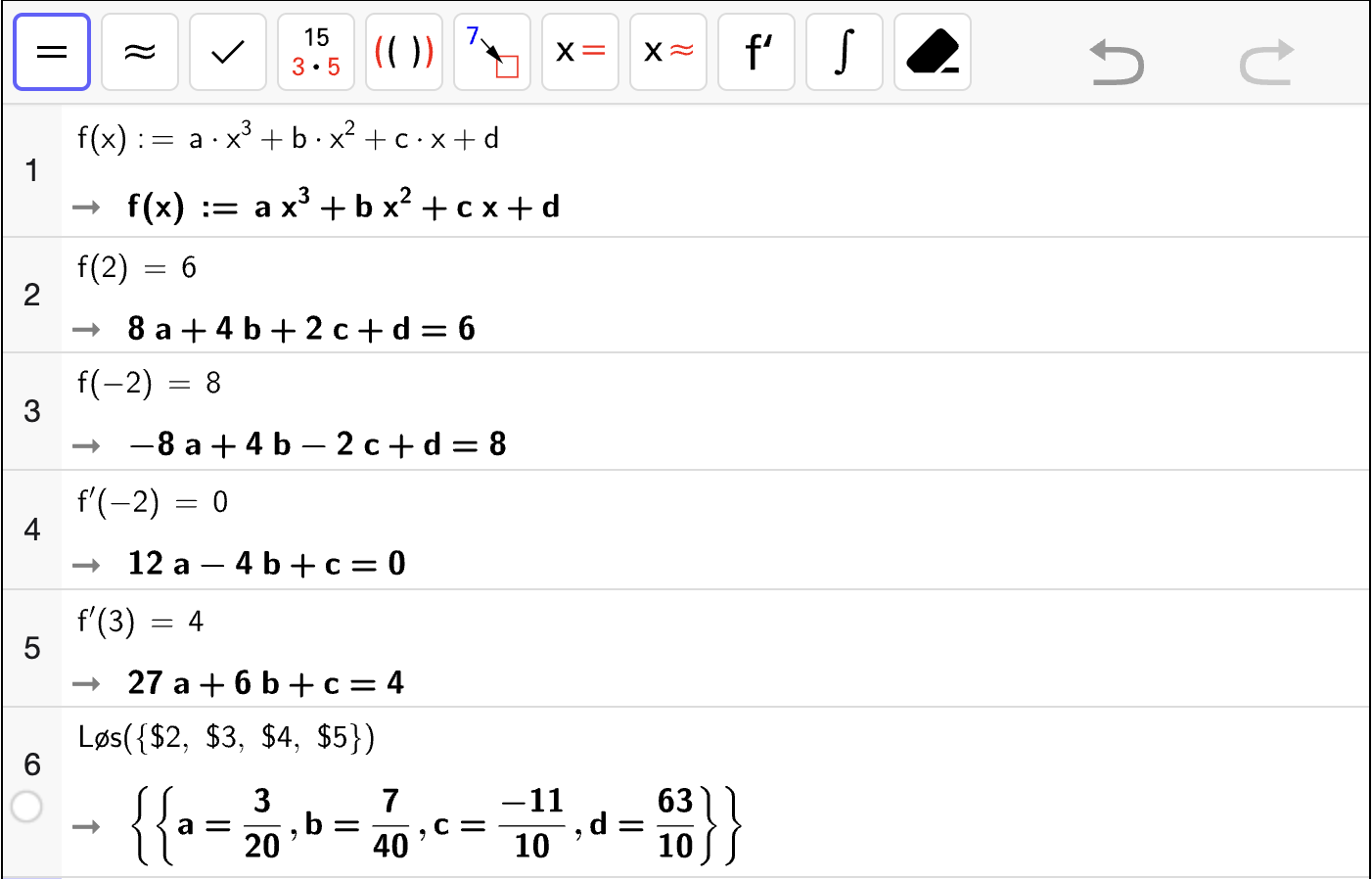
Fig. 4 viser hvordan vi først markerer likningene (klikk-og-dra) og deretter trykker på eller for å løse likningssystemet.

Bruk fremgangsmåten i figuren ovenfor til å løse likningssystemene nedenfor. Løs de både eksakt med og numerisk med .

Åpne CAS‑vindu

a

\[\begin{align*} x + 2y &= 3 \\ \\ 2x - 4y &= 8 \end{align*}\]

Ja, det er samme likningssystem som i figuren ovenfor!

Fasit

Eksakt

\[ x = \dfrac{7}{2} \and y = -\dfrac{1}{4} \]

Numerisk

\[ x \approx 3.5 \and y \approx -0.25 \]

b

\[\begin{align*} 3x - y &= 5 \\ \\ -2x + y &= 10 \end{align*}\]

Fasit

Siden løsningene er hele tall, så får vi det samme uansett om vi bruker eksakt eller numerisk løsning. Løsningen er

\[ x = 15 \and y = 40 \]

---