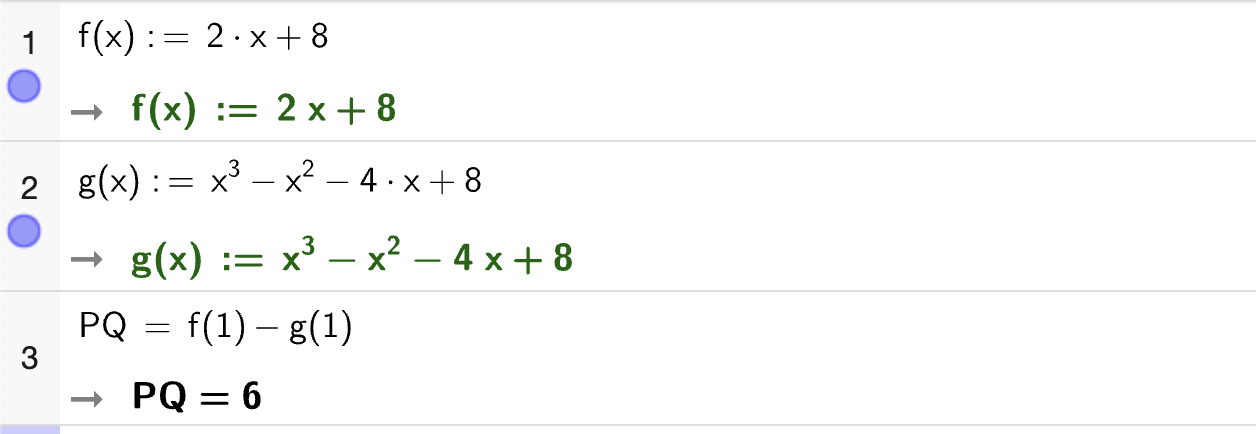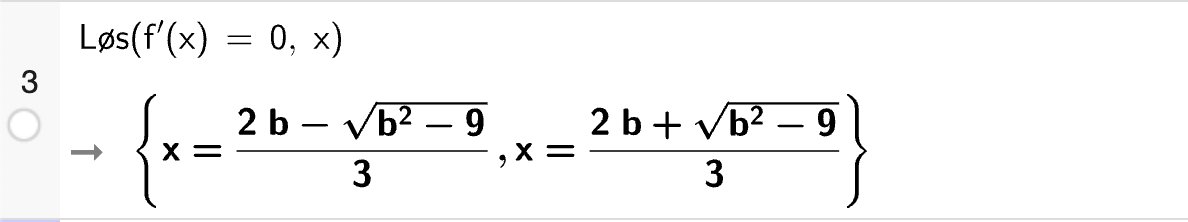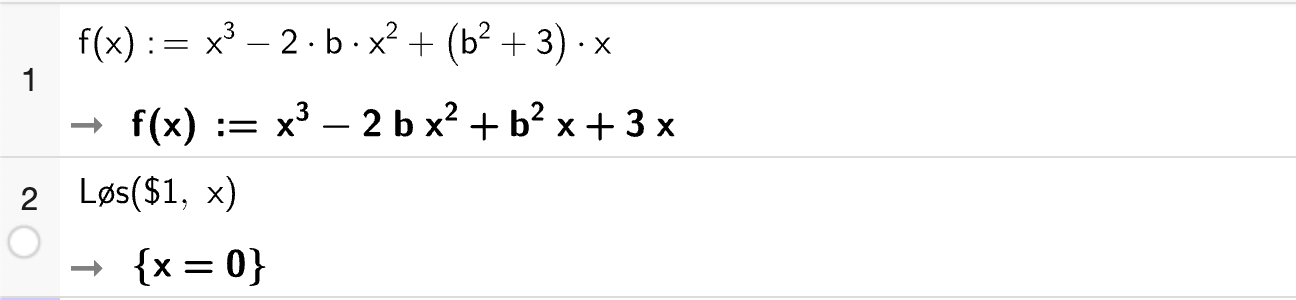CAS-kurs: Del 2

Læringsmål

• Kunne løse likninger, ulikheter og likningssystemer med CAS.

• Kunne jobbe med funksjoner i CAS til å finne funksjonsverdier, løse likninger, ulikheter, likningssystemer, bestemme den deriverte og anvende disse til å løse oppgaver.

Likninger

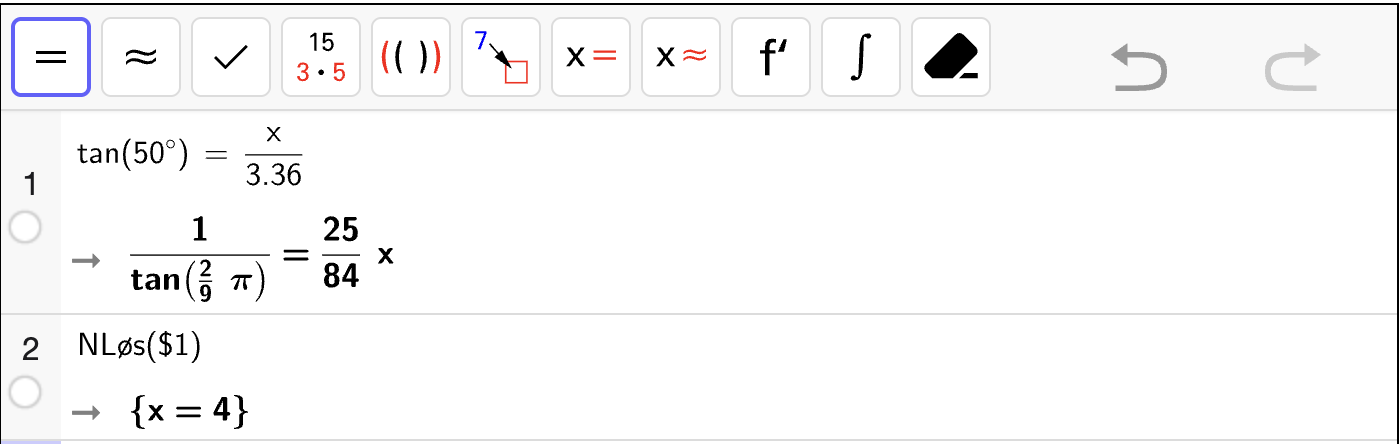
Nedenfor vises et eksempel på hvordan man løser likninger med CAS.

Utforsk 1

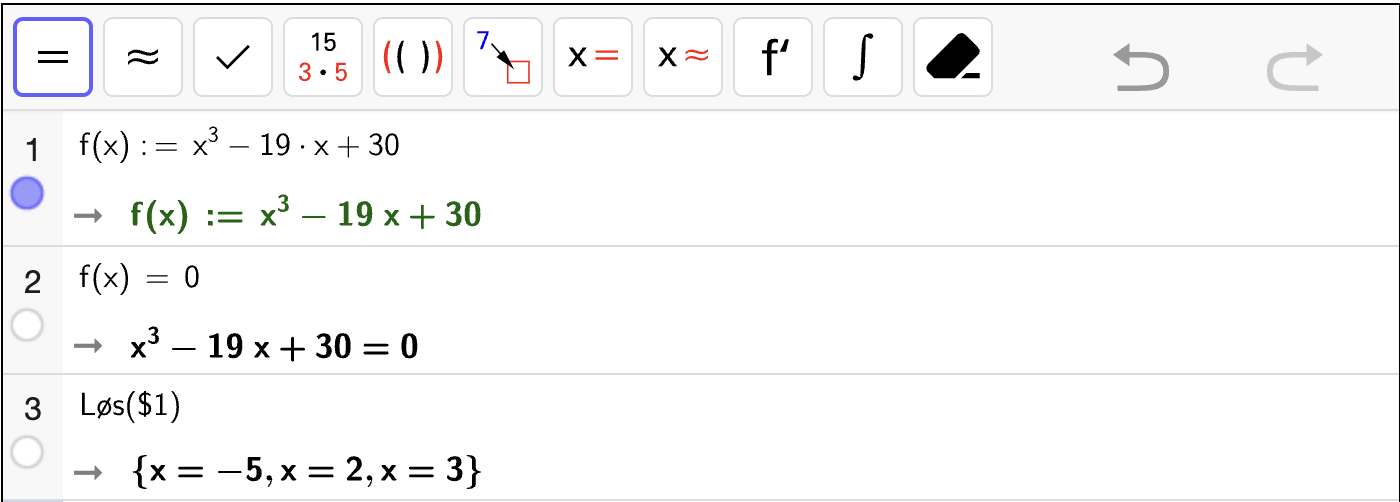
Nedenfor vises et CAS-vindu som løser likningen

\[ x^2 - x - 6 = 0. \]

Vi gjør følgende:

1. Skriver inn likningen i celle 1.

2. Bruker Løs-kommandoen til å løse likningen i celle 2. Vi skriver Løs($1) der $1 fyller inn likningen fra celle 1 for oss.

Fra utskriften i celle 2 kan vi lese av at løsningen er

\[ x = -2 \or x = 3. \]

---

Underveisoppgave 1

Bruk CAS-vinduet nedenfor til å løse likningene.

a

\[ x^2 - 3x - 4 = 0. \]

Fasit

Svar:

\[ x = -1 \or x = 4. \]

b

\[ -x^2 + 9 = 0. \]

Fasit

Svar:

\[ x = -3 \or x = 3. \]

c

\[ x^3 + 6x^2 - x - 30 = 0. \]

Fasit

Svar:

\[ x = -5 \or x = -3 \or x = 2. \]

d

\[ x^3 + x^2 - 5x + 1 = -x + 5. \]

Fasit

Svar:

\[ x = -2 \or x = -1 \or x = 2. \]

Ulikheter

Utforsk 2

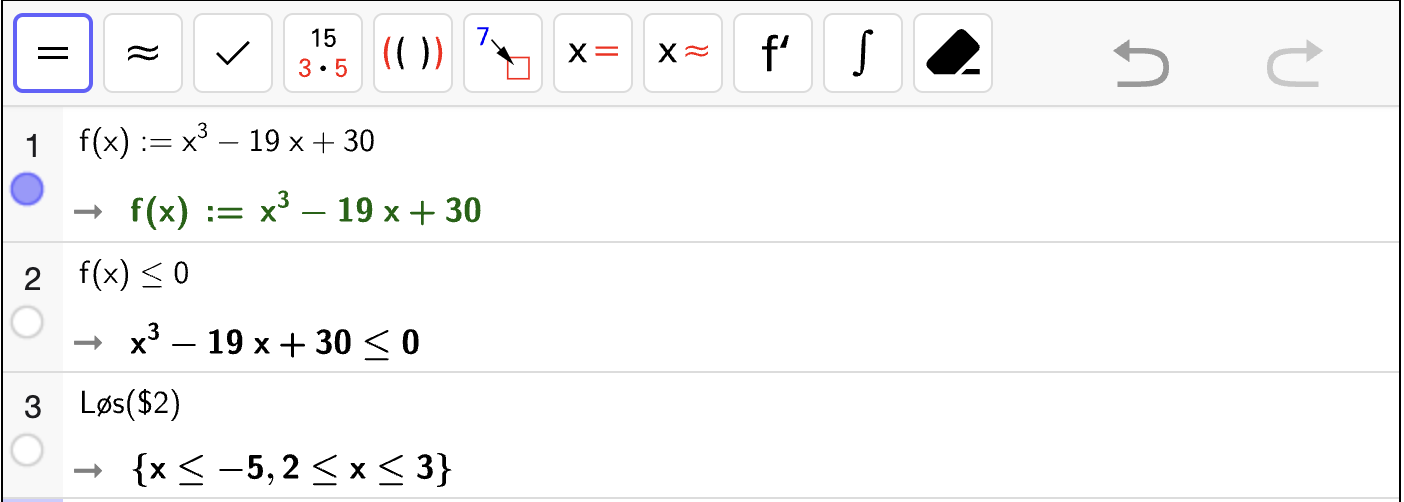
Nedenfor vises et CAS-vindu som løser ulikheten

\[ x^3 - 2x^2 - 7x - 4 < 0. \]

Vi gjør følgende:

1. Skriver inn ulikheten i celle 1.

2. Bruker Løs-kommandoen til å løse ulikheten i celle 2. Vi skriver Løs($1) der $1 fyller inn ulikheten fra celle 1 for oss.

Fra utskriften kan vi lese av at løsningen er

\[ x < -1 \or -1 < x < 4. \]

---

Underveisoppgave 2

Bruk CAS-vinduene nedenfor til å løse ulikhetene.

a

\[ (x - 1)(x + 4) \leq 0. \]

Fasit

Svar:

\[ -4 \leq x \leq 1. \]

b

\[ (x - 1)^2(x + 3) > 0. \]

Fasit

Svar:

\[ -3 < x < 1 \or x > 1. \]

c

\[ x^2 - 3x - 4 \geq 0. \]

Fasit

Svar:

\[ x \leq -1 \or x \geq 4 \]

d

\[ x^3 + x^2 - 4x - 4 \geq 0. \]

Fasit

Svar:

\[ -2 \leq x \leq -1 \or x \geq 2 \]

Likningssystemer

Utforsk 3

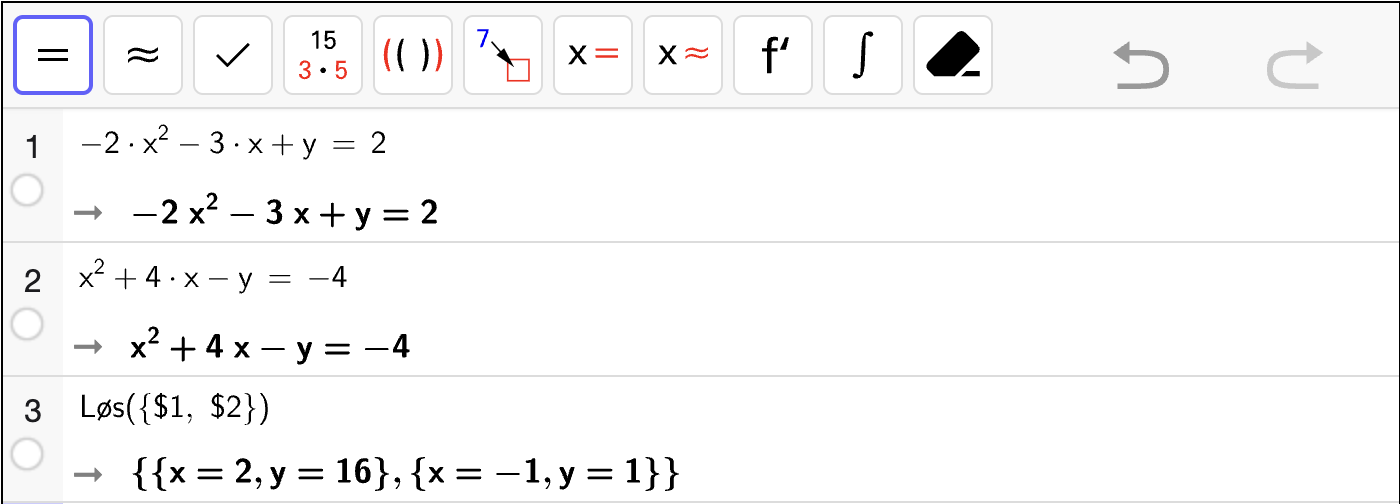
Nedenfor vises et CAS-vindu som løser likningssystemet

\[\begin{align*} 2x - y &= 1 \\ -x^2 + 3x + y &= 3 \end{align*}\]

Vi gjør følgende:

1. Vi skriver inn likningene i celle 1 og celle 2.

2. Vi bruker Løs-kommandoen til å løse likningssystemet i celle 3. Vi skriver Løs({$1, $2}) der $1 og $2 fyller inn likningene fra celle 1 og celle 2 for oss i en liste. Merk at vi lager en liste med {}-parenteser.

Fra utskriften i celle 3, kan vi lese av at løsningen av likningssystemet er

\[ x = 4 \lland y = 7 \or x = 1 \lland y = 1. \]

---

Underveisoppgave 3

a

Løs likningssystemet

\[\begin{align*} 3x + y &= 3 \\ 3x^2 - y^2 &= -9 \end{align*}\]

Fasit

Svar:

\[ x = 0 \lland y = 3 \or x = 3 \lland y = -6. \]

b

Løs likningssystemet

\[\begin{align*} -2x^2 - 3x + y &= 2 \\ x^2 + 4x - y &= -4 \end{align*}\]

Fasit

Svar:

\[ x = 2 \lland y = 16 \or x = -1 \lland y = 1. \]

c

Løs likningssystemet

\[\begin{align*} x - y &= 1 \\ -x^2 + 4x + y &= 3 \end{align*}\]

Fasit

Svar:

\[ x = 1 \lland y = 0 \or x = 4 \lland y = 3. \]

d

Løs likningssystemet

\[\begin{align*} 2x - y &= 4 \\ x^2 - 3x - 2y &= -4 \end{align*}\]

Fasit

Svar:

\[ x = 4 \lland y = 4 \or x = 3 \lland y = 2. \]

Funksjoner

Utforsk 4

Her skal vi se på hvordan vi kan jobbe med funksjoner i CAS.

Funksjonsverdier

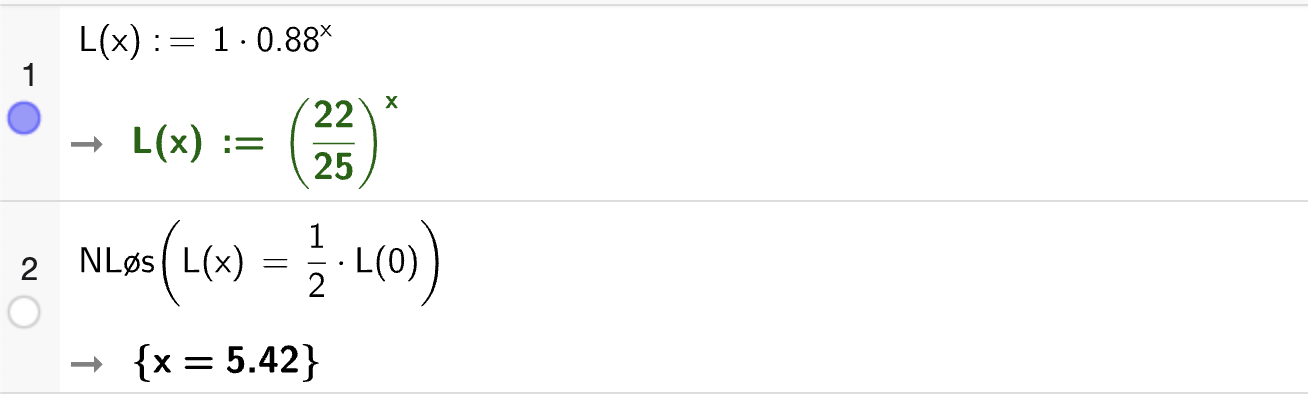
I CAS-vinduet nedenfor vises et eksempel på hvordan vi definerer en funksjon \(f(x)\) og regner ut funksjonsverdier.

• Vi definerer en funksjon ved å skrive f(x) := x^2 - 2x - 3 i celle 1. Legg merke til at vi bruker := når vi definerer en funksjon!

• I celle 2 - 4 regner vi ut funksjonsverdier med tall.

• I celle 5 regner vi ut funksjonsverdien med en variabel.

Likninger og ulikheter

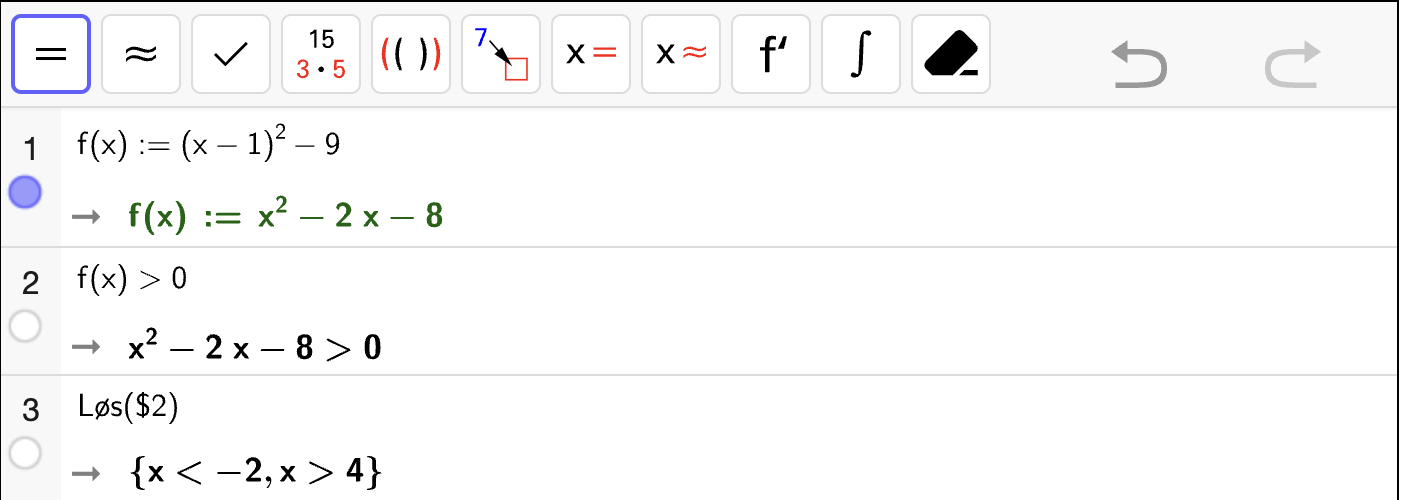
I CAS-vinduet nedenfor viser vi hvordan vi kan løse likninger og ulikheter med \(f(x)\).

• I celle 2 løser vi \(f(x) = 0\).

• I celle 3 løser vi \(f(x) \geq 0\).

• I celle 4 løser vi \(f(x) < 5\).

Underveisoppgave 4

En funksjon \(f\) er gitt ved

\[ f(x) = x^3 - 2x^2 - 7x - 4. \]

a

Definer en funksjon \(f\) og regn ut funksjonsverdiene \(f(0)\), \(f(1)\), \(f(-2)\) og \(f(k)\).

Fasit

b

Løs likningen

\[ f(x) = 0. \]

Fasit

Svar:

\[ x = -1 \or x = 4. \]

c

Løs ulikheten

\[ f(x) \geq 0. \]

Fasit

Svar:

\[ x = -1 \or x \geq 4. \]

---

Utforsk 5

Her skal vi se på hvordan vi kan bestemme \(f(x)\) fra opplysninger om en funksjon \(f\).

En tredjegradsfunksjon \(f\) er gitt ved

\[ f(x) = ax^3 + bx^2 + cx + d \]

a

Grafen til \(f\) går gjennom punktet \((2, -4)\).

Sett opp én eller flere likninger som passer med opplysningen.

Fasit

\[ f(2) = -4. \]

b

Punktet \((-1, -4)\) er et bunnpunkt på grafen til \(f\).

Sett opp én eller flere likninger som passer med opplysningen.

Fasit

• \(f(-1) = -4\) (fordi punktet ligger på grafen til \(f\)).

• \(f'(-1) = 0\) (fordi det er et bunnpunkt på grafen til \(f\)).

c

Tangenten til grafen til \(f\) i punktet \((0, f(0))\) har stigningstall \(3\).

Sett opp én eller flere likninger som passer med opplysningen.

Fasit

\[ f'(0) = 3. \]

d

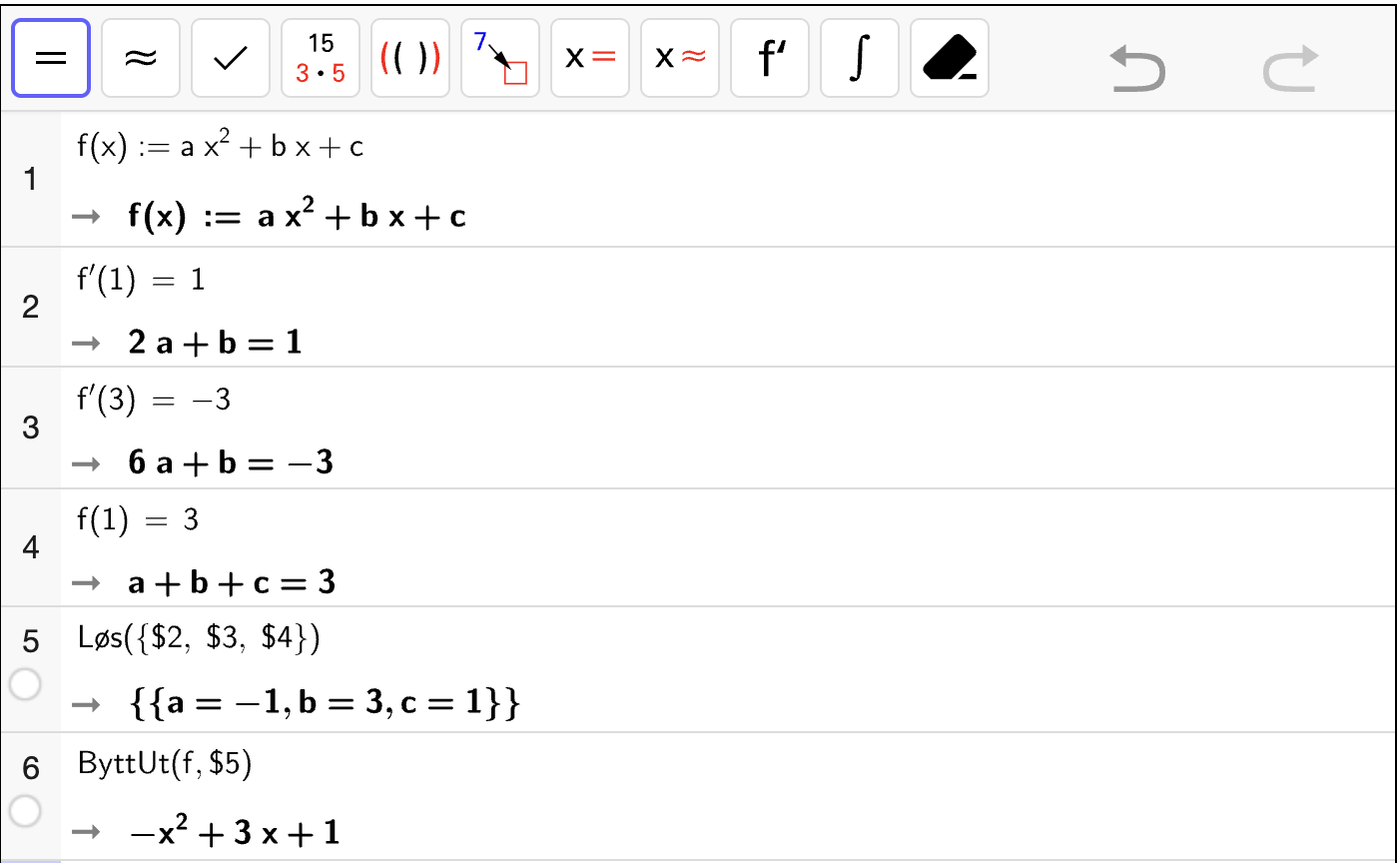
I CAS-vinduet nedenfor er tredjegradsfunksjon \(f\) definert og to av likningene er skrevet inn.

Fyll ut CAS-vinduet og bestem \(a\), \(b\), \(c\) og \(d\) ved å løse likningssystemet.

Hva var likningene igjen?

• \(f(2) = -4\)

• \(f(-1) = -4\)

• \(f'(-1) = 0\)

• \(f'(0) = 3\)

Fasit

Svar:

\[ a = -1 \and b = 0 \and c = 3 \and d = -2. \]

---

Underveisoppgave 5

En tredjegradsfunksjon \(f\) er gitt ved

\[ f(x) = ax^3 + bx^2 + cx + d. \]

Om \(f\) får du vite at

• Grafen til \(f\) skjærer \(x\)-aksen i \(x = 2\).

• Punktet \((-3, 0)\) er et toppunkt på grafen til \(f\).

• Tangenten til grafen til \(f\) i punktet \((1, f(1))\) har stigningstall \(8\).

a

Sett opp likninger som passer med opplysningene om \(f\).

Fasit

Likningene blir

1. \(f(2) = 0\).

2. \(f(-3) = 0\).

3. \(f'(-3) = 0\).

4. \(f'(1) = 8\).

b

Bestem \(a\), \(b\), \(c\) og \(d\).

Fasit

Svar:

\[ x = 1 \and b = 4 \and c = -3 \and d = -18 \]

---

Utforsk 6

Her skal vi se på et eksempel der vi skal bruke CAS til å løse en optimeringsoppgave.

I Fig. 1 vises grafen til en andregradsfunksjon \(f\) som er gitt ved

\[ f(x) = -x^2 + 9, \]

der \(D_f = [0, 3]\), og en trekant som har hjørner i punktene \((0, 0)\), \((k, 0)\) og \((k, f(k))\).

Fig. 1 viser grafen til \(f(x) = -x^2 + 9\) for \(x \in [0, 3]\) og en trekant med hjørner i \((0, 0)\), \((k, 0)\) og \((k, f(k))\).

a

Bestem arealet \(A(k)\) til uttrykt ved \(f(k)\) og \(k\).

Fasit

\[ A(k) = \dfrac{k\cdot f(k)}{2} \]

b

Sett opp en likning som kan brukes til å bestemme den verdien av \(k\) som gir størst mulig areal for trekanten.

Fasit

\[ A'(k) = 0. \]

c

I CAS-vinduet nedenfor har vi definert \(f(x)\) og \(A(k)\).

Fyll ut CAS-vinduet og bruk det til å bestemme den verdien av \(k\) som gir størst mulig areal for trekanten.

Fasit

Svar:

\[ k = \sqrt{3} \]

---

Underveisoppgave 6

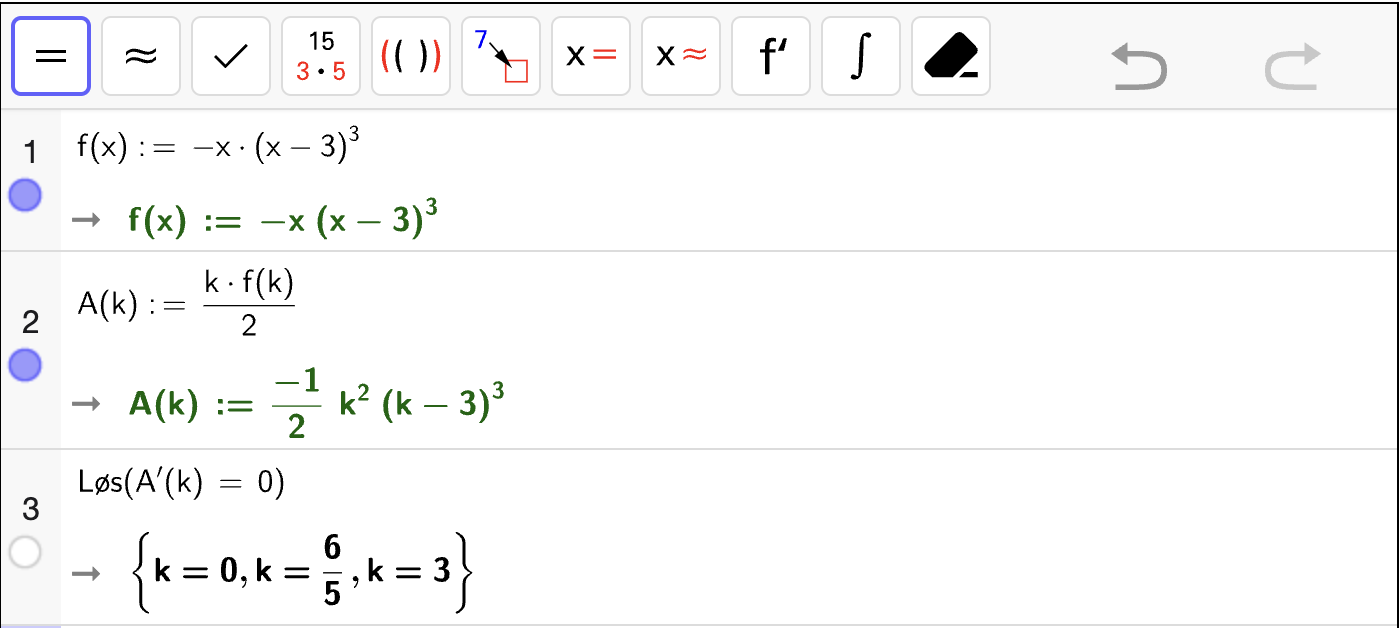
En fjerdegradsfunksjon \(f\) er gitt ved

\[ f(x) = -x(x - 3)^3, \quad D_f = [0, 3]. \]

En trekant har hjørner i \((0, 0)\), \((k, 0)\) og \((k, f(k))\). Se Fig. 2.

Bestem den verdien av \(k\) som gir størst mulig areal for trekanten.

Fig. 2 viser grafen til \(f(x) = -x(x - 3)^3\) for \(x \in [0, 3]\) og en trekant med hjørner i \((0, 0)\), \((k, 0)\) og \((k, f(k))\).

Fasit

Svar:

\[ k = \dfrac{6}{5} \]

Oppgaver

Oppgave 1

En andregradsfunksjon \(f\) er gitt ved

\[ f(x) = (x - 1)^2 - 9. \]

Løs oppgavene nedenfor med CAS.

a

Regn ut \(f(-4)\).

Fasit

Svar:

\[ f(-4) = 16. \]

b

Finn nullpunktene til \(f\).

Fasit

Svar:

\[ x = -2 \or x = 4. \]

c

Bestem ekstremalpunktet til \(f\).

Fasit

Svar:

\[ x = 1. \]

d

Løs ulikheten \(f(x) > 0\).

Fasit

Svar:

\[ x < -2 \or x > 4. \]

---

Oppgave 2

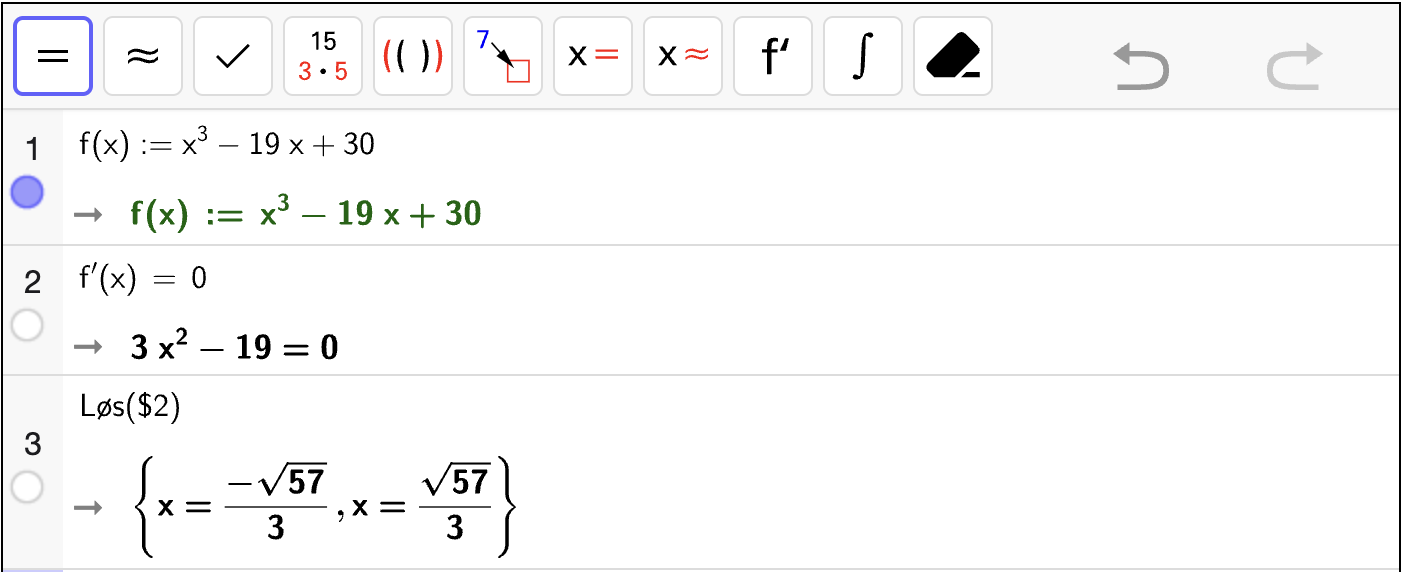
En tredjegradsfunksjon \(f\) er gitt ved

\[ f(x) = x^3 - 19x + 30. \]

a

Bestem i hvilke punkter grafen til \(f\) skjærer \(x\)-aksen.

Fasit

Svar:

\[ x = -5 \or x = 2 \or x = 3. \]

b

Faktoriser \(f(x)\).

Hint: Du kan bruke en funksjon i CAS som heter Faktoriser(f) til å faktorisere \(f(x)\).

Fasit

Svar:

\[ f(x) = (x - 2)(x - 3)(x + 5). \]

c

Løs ulikheten \(f(x) \leq 0\).

Fasit

Svar:

\[ x \leq -5 \or 2 \leq x \leq 3. \]

d

Bestem ekstremalpunktene til \(f\).

Fasit

Svar:

\[ x = -\dfrac{\sqrt{57}}{3} \or x = \dfrac{\sqrt{57}}{3} \]

---

Oppgave 3

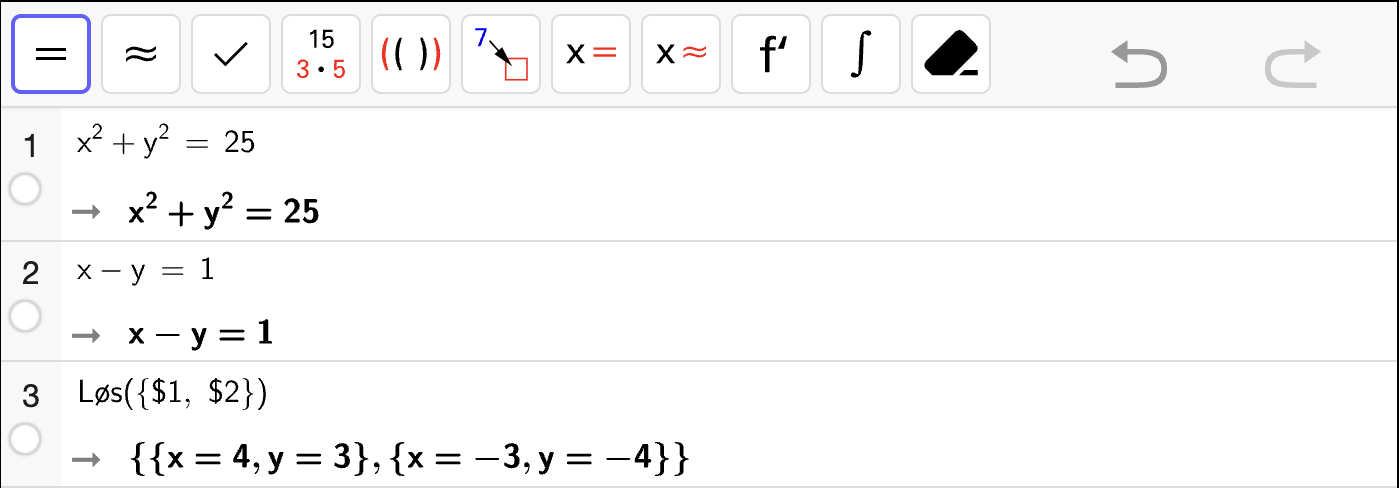
Et likningssystem er gitt ved

\[ x^2 + y^2 = 25 \and x - y = 1. \]

I Fig. 3 vises en grafisk representasjon av de to likningene.

Fig. 3 viser en grafisk representasjon av likningene \(x^2 + y^2 = 25\) og \(x - y = 1\).

a

Bruk Fig. 3 til å bestemme løsningen av likningssystemet.

Fasit

\[ x = -3 \lland y = -4 \or x = 4 \lland y = 3. \]

b

Bruk innsettingsmetoden til å bestemme løsningen av likningssystemet.

Fasit

\[ x = -3 \lland y = -4 \or x = 4 \lland y = 3. \]

Løsning

Likning 2 gir oss

\[ x - y = 1 \liff y = x - 1. \]

Vi setter inn dette uttrykket for \(y\) i likning 1:

\[\begin{align*} x^2 + y^2 &= 25 \\ \\ x^2 + (x - 1)^2 &= 25 \\ \\ x^2 + x^2 - 2x + 1 &= 25 \\ \\ 2x^2 - 2x - 24 &= 0 \\ \\ x^2 - x - 12 &= 0 \end{align*}\]

som gir

\[ x = \dfrac{1 \pm \sqrt{1 + 4 \cdot 12}}{2} = \dfrac{1 \pm 7}{2} \]

som betyr at

\[ x = -3 \or x = 4. \]

Kombinerer vi disse løsningene med \(y = x - 1\), får vi:

\[ x = -3 \implies y = -3 - 1 = -4 \]

og

\[ x = 4 \implies y = 4 - 1 = 3. \]

Dermed er løsningene av likningssystemet gitt ved

\[ x = -3 \lland y = -4 \or x = 4 \lland y = 3. \]

c

Bruk CAS-vindu nedenfor til å løse likningssystemet.

Fasit

Svar:

\[ x = -3 \lland y = -4 \or x = 4 \lland y = 3. \]

---

Oppgave 4

Om en tredjegradsfunksjon \(f\) gitt ved

\[ f(x) = ax^3 + bx^2 + cx + d \]

får du vite at

• Grafen til \(f\) går gjennom punktet \((2, 6)\).

• Punktet \((-2, 8)\) er et toppunkt på grafen til \(f\).

• Tangenten til grafen til \(f\) i punktet \((3, f(3))\) har stigningstall \(4\).

a

Sett opp et likningssystem som passer med opplysningene om \(f\).

Fasit

• \(f(2) = 6\).

• \(f(-2) = 8\).

• \(f'(-2) = 0\).

• \(f'(3) = 4\).

b

Bruk likningssystemet fra oppgave a til å bestemme koeffisientene \(a\), \(b\), \(c\) og \(d\).

Fasit

Svar:

\[ a = \dfrac{3}{20} \lland b = \dfrac{7}{40} \lland c = -\dfrac{11}{10} \lland d = \dfrac{63}{10} \]

---

Oppgave 5

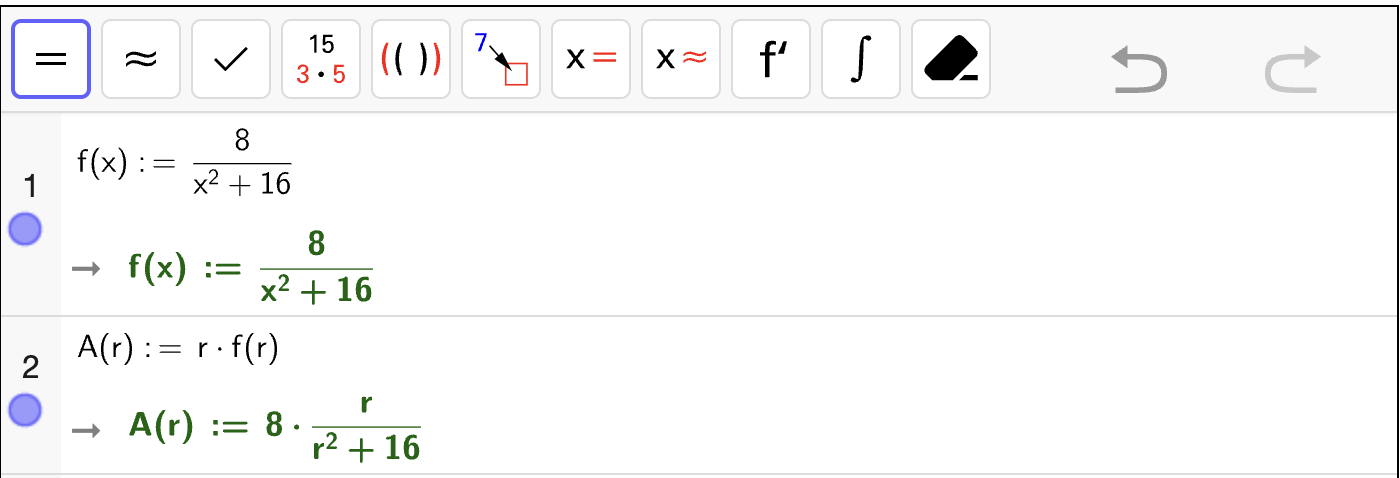
En rasjonal funksjon \(f\) er gitt ved

\[ f(x) = \dfrac{8}{x^2 + 16} \quad \text{der} \quad D_f = [0, \to\rangle \]

Et rektangel har hjørner i \((0, 0)\), \((r, 0)\), \((r, f(r))\) og \((0, f(r))\).

a

Lag en modell \(A\) som beskriver arealet \(A(r)\) til rektangelet.

Fasit

Svar:

\[ A(r) = \dfrac{8r}{r^2 + 16} \]

b

Bestem \(r\) slik at arealet blir størst mulig.

Fasit

Svar:

\[ r = 4. \]

---

Oppgave 6

I Fig. 4 vises grafen til en andregradsfunksjon \(f\) og to tangenter.

• Tangenten i \((1, f(1))\) har stigningstall \(1\).

• Tangenten i \((3, f(3))\) har stigningstall \(-3\).

• Tangentene skjærer hverandre i \((2, 4)\).

Fig. 4 viser grafen til en andregradsfunksjon \(f\) og to tangenter gjennom \((1, f(1))\) og \((3, f(3))\).

a

Sett opp et likningssystem for \(f(x)\) ut ifra opplysningene.

Fasit

• \(f(x) = ax^2 + bx + c\).

• \(f'(1) = 1\)

• \(f'(3) = -3\).

• \(f(1) = 3\).

b

Bestem \(f(x)\).

Fasit

Svar:

\[ f(x) = -x^2 + 3x + 1. \]