Oppgaver: Arealsetningen

Oppgave 1

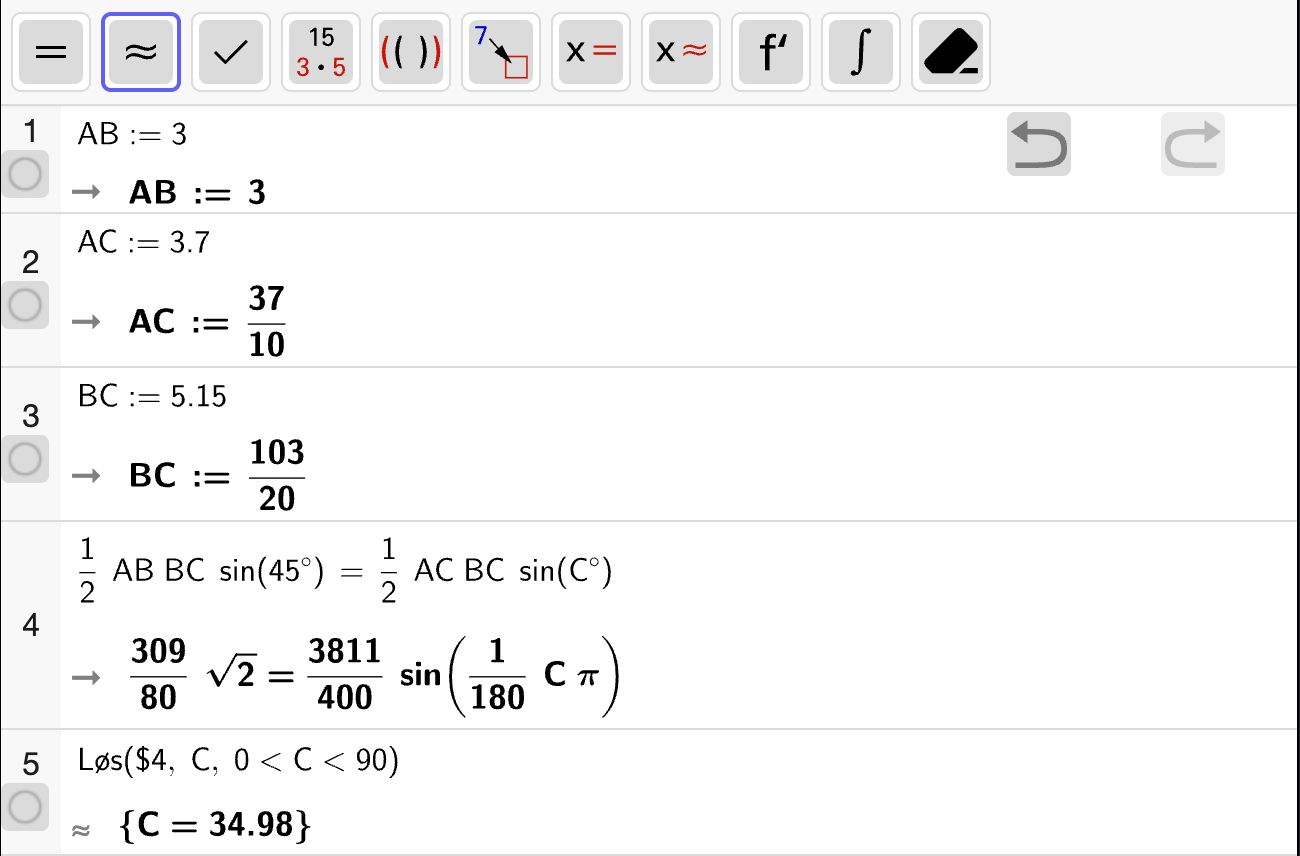
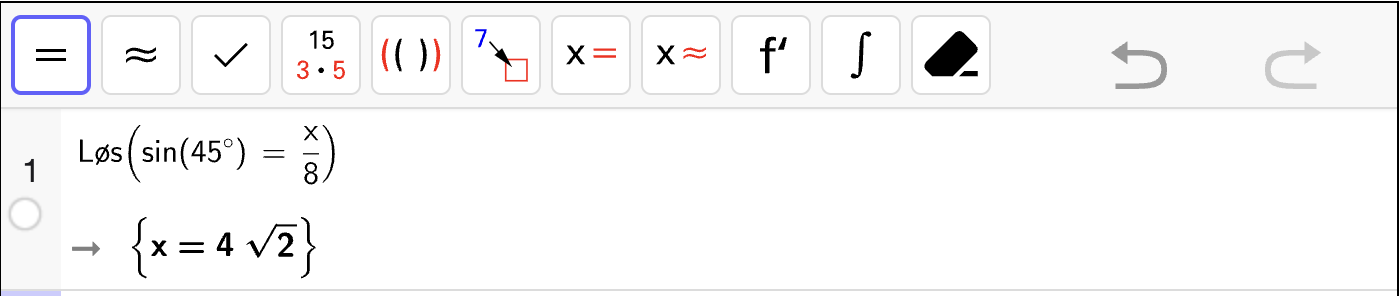
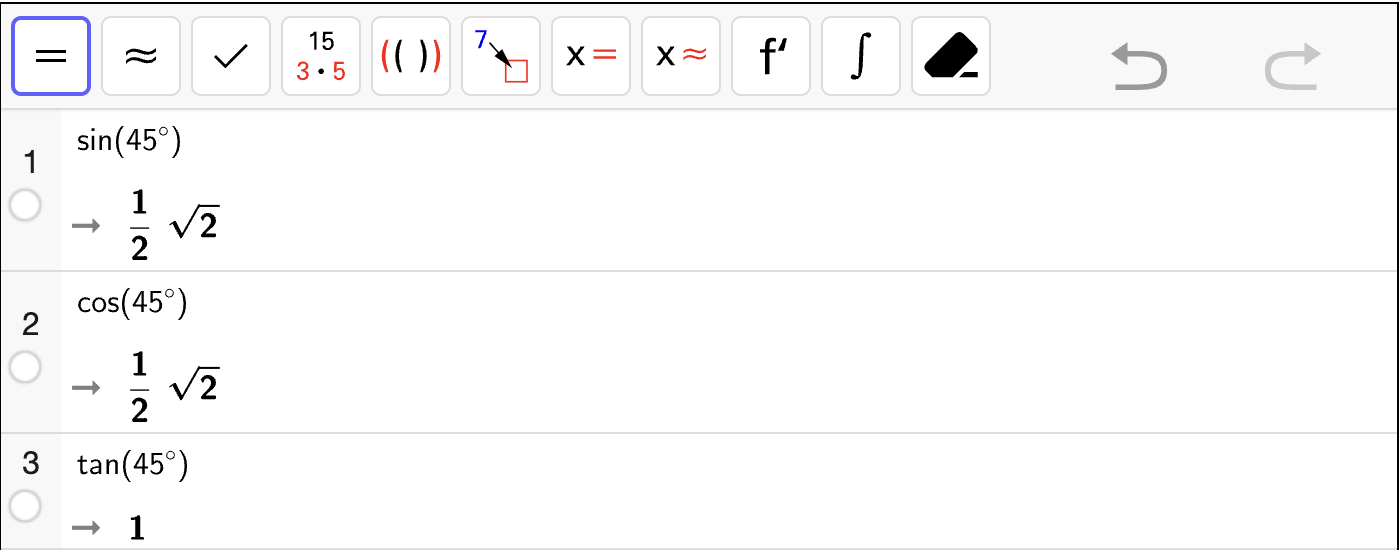
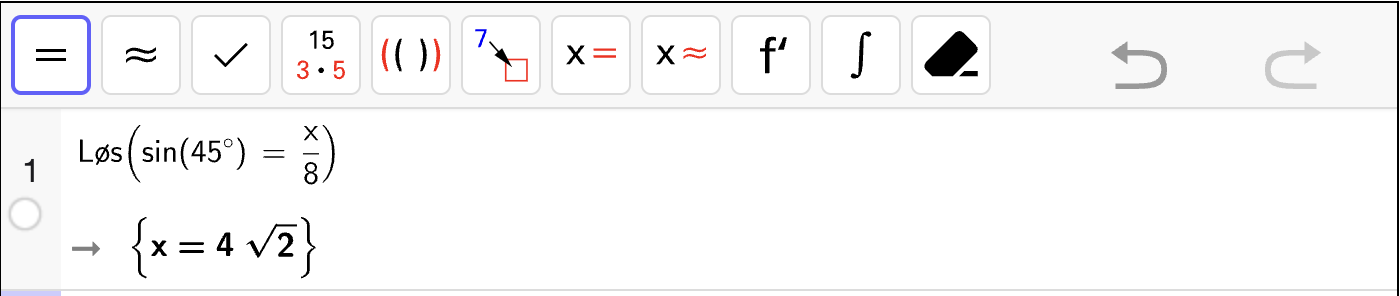
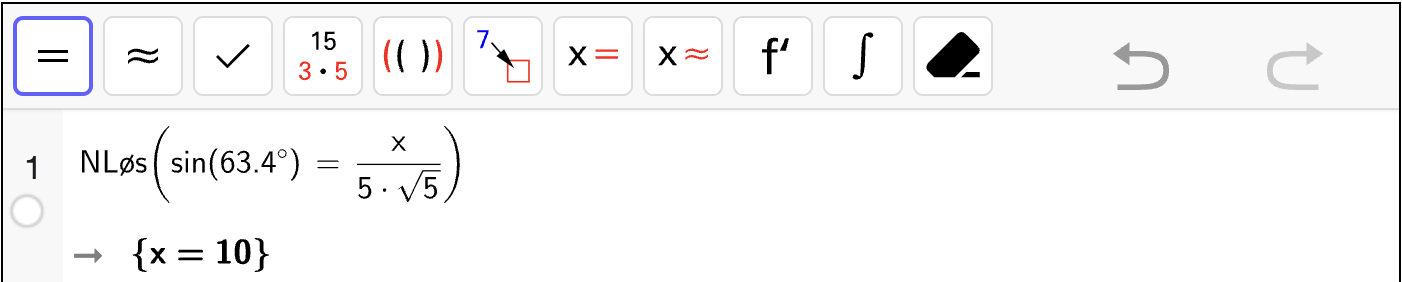
Her trenger du CAS til å regne ut \(\sin v\).

Åpne CAS‑vindu

a

Bestem arealet av trekanten nedenfor.

Fasit

Arealet er derfor

\[ T = \dfrac{3 \sqrt{3}}{2} \]

b

Bestem arealet av trekanten nedenfor.

Fasit

Arealet er derfor

\[ T \approx 3.22 \]

c

Bestem arealet av trekanten nedenfor.

Fasit

Arealet er derfor

\[ T \approx 5.75. \]

---

Oppgave 2

Åpne CAS‑vindu

a

Bestem \(\angle A\) i trekanten nedenfor.

Hint

Lag en likning ved å bestemme arealet av trekanten på to måter, og sett dem lik hverandre!

CAS-vindu

Fasit

Altså er \(\angle A \approx 30.13 \degree\).

b

Bestem \(\angle C\) i trekanten nedenfor.

Fasit

Altså er \(\angle C \approx 34.98 \degree\).

c

Bestem \(\angle B\) i trekanten nedenfor.

Fasit

Vinkel \(\angle B\) er spiss, så \(\angle B \approx 35.52 \degree\).

---

Oppgave 3

Åpne CAS‑vindu

a

I en \(\triangle ABC\) er \(AB = 8\), \(AC = 6\) og \(\angle A = 30 \degree\).

Bestem arealet av trekanten.

Fasit

\[ T_{\triangle ABC} = 12 \]

Løsning

Altså er arealet av \(\triangle ABC\) gitt ved

\[ T_{\triangle ABC} = 12 \]

b

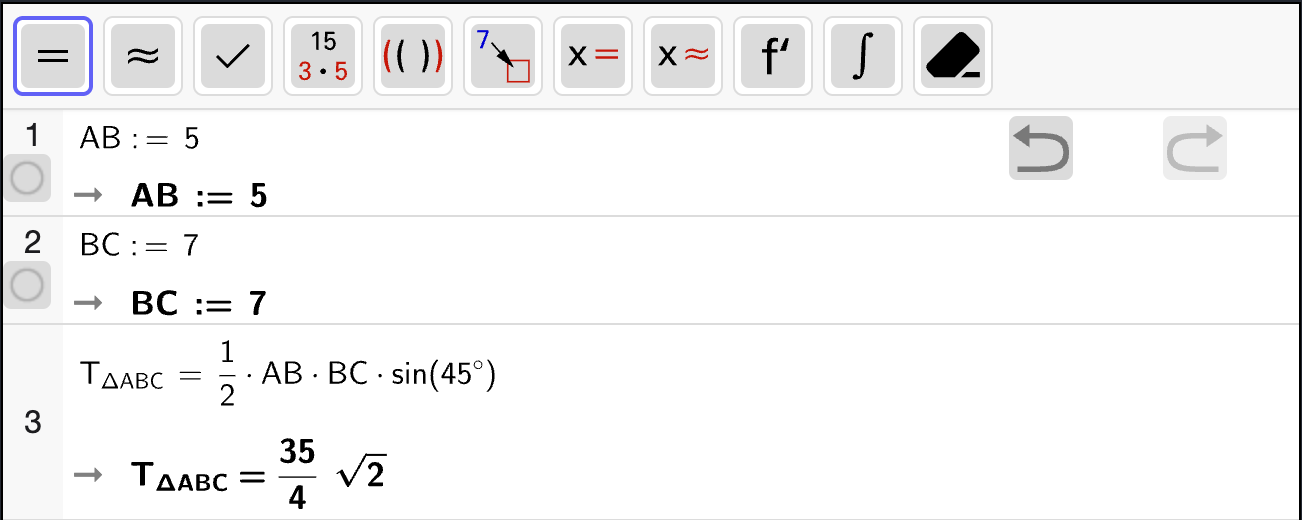
I en \(\triangle ABC\) er \(AB = 5\), \(BC = 7\) og \(\angle B = 45 \degree\).

Bestem arealet av trekanten.

Fasit

\[ T_{\triangle ABC} = \dfrac{35}{4}\sqrt{2} \]

Løsning

c

I en \(\triangle ABC\) er \(BC = 10\), \(AC = 8\) og \(\angle C = 120 \degree\).

Bestem arealet av trekanten.

Fasit

\[ T_{\triangle ABC} = 20 \sqrt{3} \]

Løsning

---

Oppgave 4

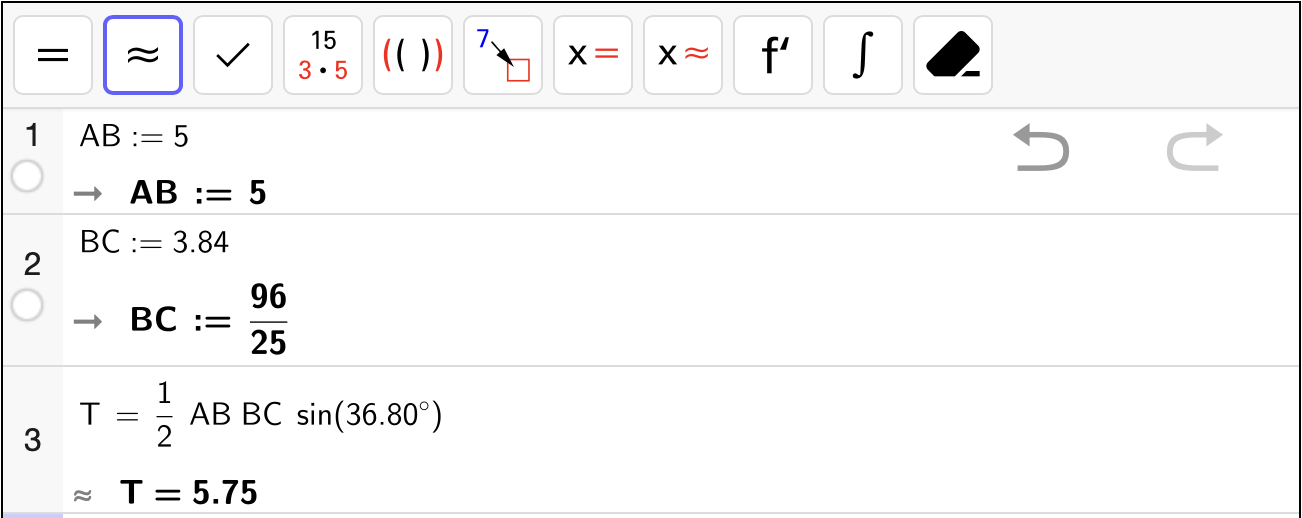
Nedenfor vises en skisse av en boligtomt.

Bestem arealet av tomten.

Åpne CAS‑vindu

Fasit

Arealet av tomta er

\[ T \approx 152.45 \; \mathrm{m}^2. \]

Løsning

Arealet av tomta er derfor

\[ T \approx 152.45 \; \mathrm{m}^2. \]

---

Oppgave 5

Nedenfor vises en sirkel med radius \(2\). Tre trekanter \(\triangle SAC\), \(\triangle CSB\) og \(\triangle CAS\) er tegnet inn i sirkelen. Punktet \(S\) er i sentrum av sirkelen og \(\angle ASB = 120 \degree\).

Åpne CAS‑vindu

a

Bestem en eksakt verdi for arealet av \(\triangle SAB\).

Fasit

Arealet er

\[ T_{SAB} = \sqrt{3}. \]

Løsning

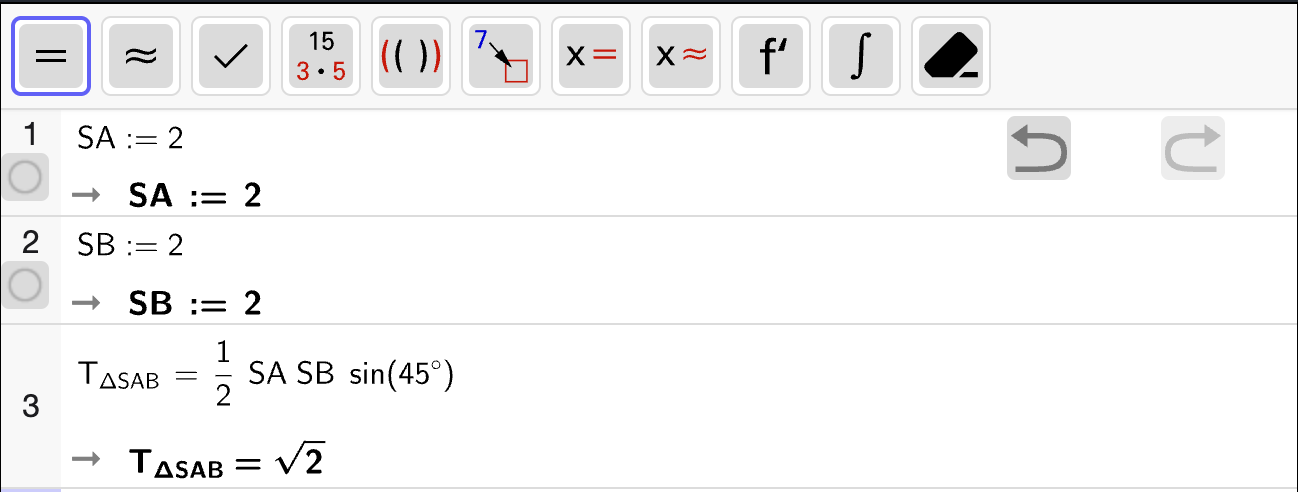
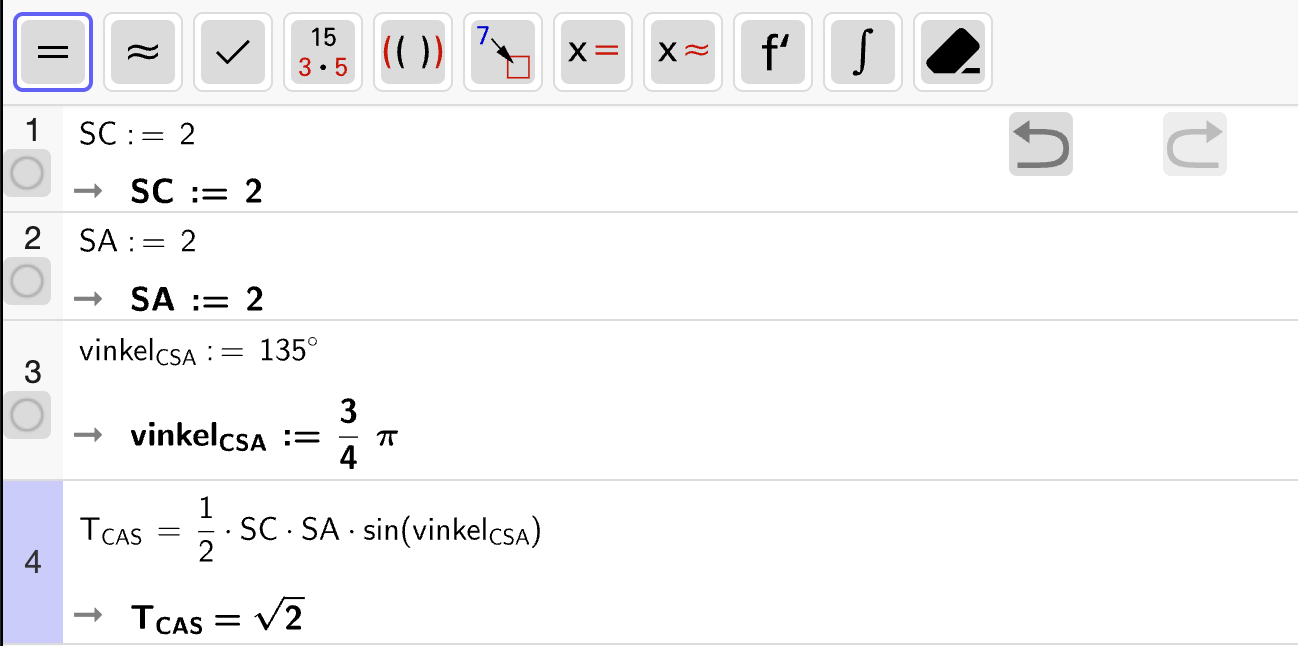
Vi kan bruke arealsetningen med \(\angle ASB = 120\degree\) som utgangspunkt. Sidene som spenner ut vinkelen er \(SA = SB = 2\). Arealet av trekanten er derfor

\[ T_{SAB} = \dfrac{1}{2} \cdot SA \cdot SB \cdot \sin (120 \degree) \]

vi regner ut med CAS og får:

Dermed er arealet av \(\triangle SAB\)

\[ T_{SAB} = \sqrt{3}. \]

b

Bestem en eksakt verdi for arealet av \(\triangle CAB\).

Fasit

Arealet er

\[ T_{CAB} = 2\sqrt{3}. \]

Løsning

Trekant \(\triangle CAB\) består av to trekanter \(\triangle CSB\) og \(\triangle SAB\). Begge trekanter har samme grunnlinje siden \(CS = SA = 2\) og høyde siden de har samme “toppunkt” \(B\) som betyr at de to trekantene har samme areal. Derfor er arealet av \(\triangle CAB\) er det dobbelte av arealet til \(\triangle SAB\). Dermed har vi at

\[ T_{CAB} = 2\cdot T_{SAB} = 2 \sqrt{3}. \]

---

Oppgave 6

Nedenfor vises en firkant \(\square ABCD\).

Åpne CAS‑vindu

a

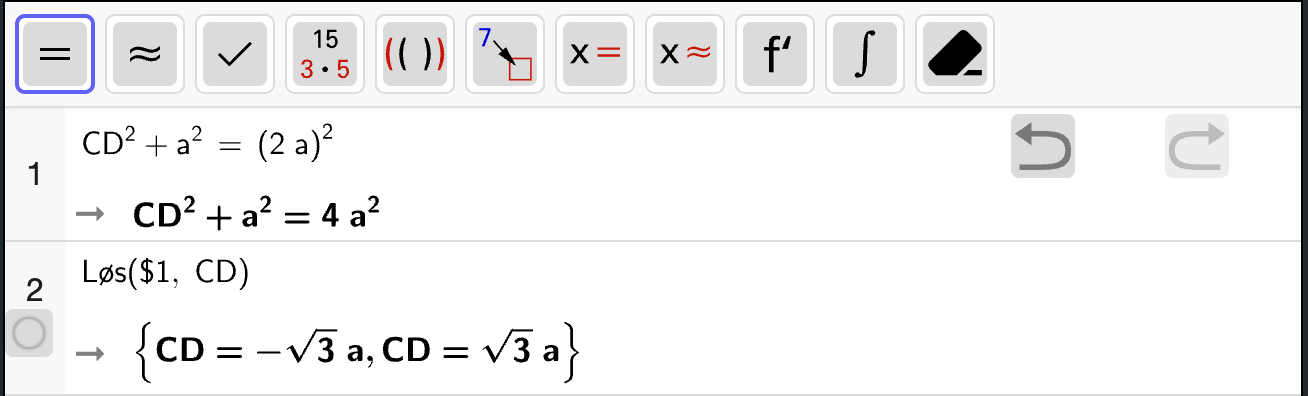
Bestem en eksakt verdi for lengden av \(CD\) uttrykt ved \(a\).

Fasit

\[ CD = \sqrt{3} \cdot a \]

Løsning

Vi kan observere at \(\triangle ACD\) er en rettvinklet trekant slik at vi kan bruke Pytagoras’ setning med:

\[ CD^2 + AD^2 = AC^2. \]

Vi regner ut med CAS:

Vi må velge den positive løsningen siden dette er en lengde. Dermed har vi at

\[ AD = \sqrt{3} \cdot a. \]

b

Bestem en eksakt verdi for arealet av firkanten uttrykt ved \(a\).

Fasit

\[ T_{\square ABCD} = \dfrac{1}{2}\left(3 + \sqrt{3}\right) \cdot a^2 \]

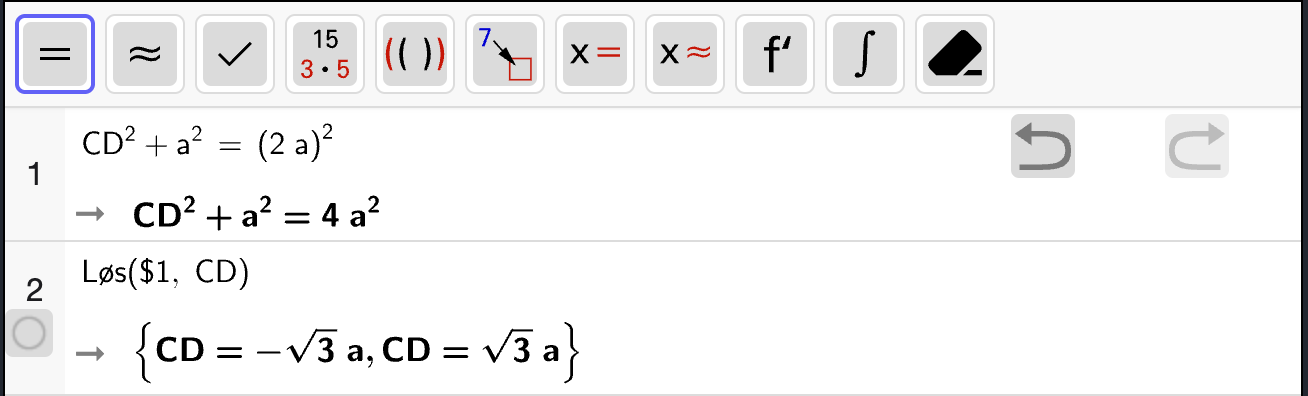
Løsning

Først kan vi merke oss at \(\square ABCD\) består av to trekanter \(\triangle ACD\) og \(\triangle ABC\). Vi kan derfor regne ut arealet av \(\square ABCD\) ved å summere arealene til de to trekantene.

Arealet av \(\triangle ACD\) er gitt ved

\[ T_{\triangle ACD} = \dfrac{1}{2} \cdot AD \cdot CD \]

Vi regner ut med CAS:

Videre kan vi merke oss at \(\triangle ACD\) er en \(30\degree\)-\(60\degree\)-\(90\degree\) trekant siden \(\angle ACD = 90\degree\) og den korteste kateten er halvparten så lang som hypotenusen. Det er \(\angle ACD = 30 \degree\).

Dermed følger det at

\[ \angle ACD + \angle BCA = 150 \degree \liff \angle BCA = 150\degree - 30\degree = 120 \degree. \]

Arealet av \(\triangle ABC\) kan derfor regnes ut ved

\[ T_{\triangle ABC} = \dfrac{1}{2} \cdot BC \cdot AC \cdot \sin(120 \degree). \]

Vi regner ut med CAS:

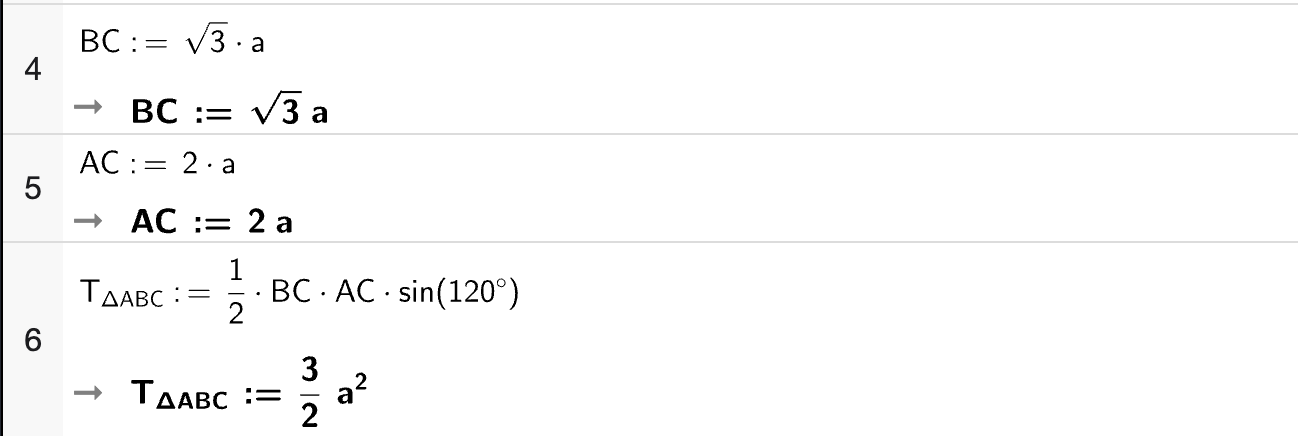
Til slutt summerer vi de to arealene for å finne arealet \(T_{\square ABCD}\). Vi får:

Altså er

\[ T_{\square ABCD} = \dfrac{1}{2}\left(3 + \sqrt{3}\right) \cdot a^2 \]

c

Bestem en eksakt verdi for \(a\) slik at arealet av firkanten er \(3\).

Fasit

\[ a = \sqrt{3 - \sqrt{3}} \]

Løsning

Arealet \(T_{\square ABCD}(a)\) er en funksjon av \(a\) slik at vi kan bestemme \(a\) ved å løse likningen

\[ T_{\square ABCD}(a) = 3. \]

Vi gjør dette med CAS:

som betyr arealet til firkanten er \(3\) dersom

\[ a = \sqrt{3 - \sqrt{3}} \]

---

Oppgave 7

Nedenfor vises en sirkel med radius \(2\) og tre trekanter \(\triangle SAB\), \(\triangle CAS\) og \(\triangle CAB\). Punktet \(S\) er i sentrum av sirkelen og \(\angle ACS = 22.5 \degree\).

Åpne CAS‑vindu

a

Bestem en eksakt verdi for arealet av \(\triangle CAS\).

Fasit

\[ T_{\triangle CAS} = \sqrt{2}. \]

Løsning

Fra figuren har vi at \(\angle ACS = 22.5 \degree\). Siden hjørnene \(C\) og \(A\) ligger på sirkelen og \(S\) er i sentrum av sirkelen, følger det at \(SC = SA = 2\). Dermed er \(\triangle CAS\) en likebeint trekant med \(S\) som toppunkt som betyr at

\[ \angle CSA + 2\cdot 22.5 \degree = 180 \degree \liff \angle CSA = 135 \degree. \]

Nå kjenner vi til vinkelen \(\angle CSA\) og sidene som spenner ut vinkelen \(SC = SA = 2\). Dermed kan vi bruke arealsetningen til å finne arealet av \(\triangle CAS\):

\[ T_{\triangle CAS} = \dfrac{1}{2} \cdot SC \cdot SA \cdot \sin(135 \degree). \]

Vi regner ut svaret med CAS:

Altså er arealet av \(\triangle CAS\)

\[ T_{\triangle CAS} = \sqrt{2}. \]

b

Bestem en eksakt verdi for arealet av \(\triangle CAB\).

Fasit

\[ T_{\triangle CAB} = 2\sqrt{2}. \]

Løsning

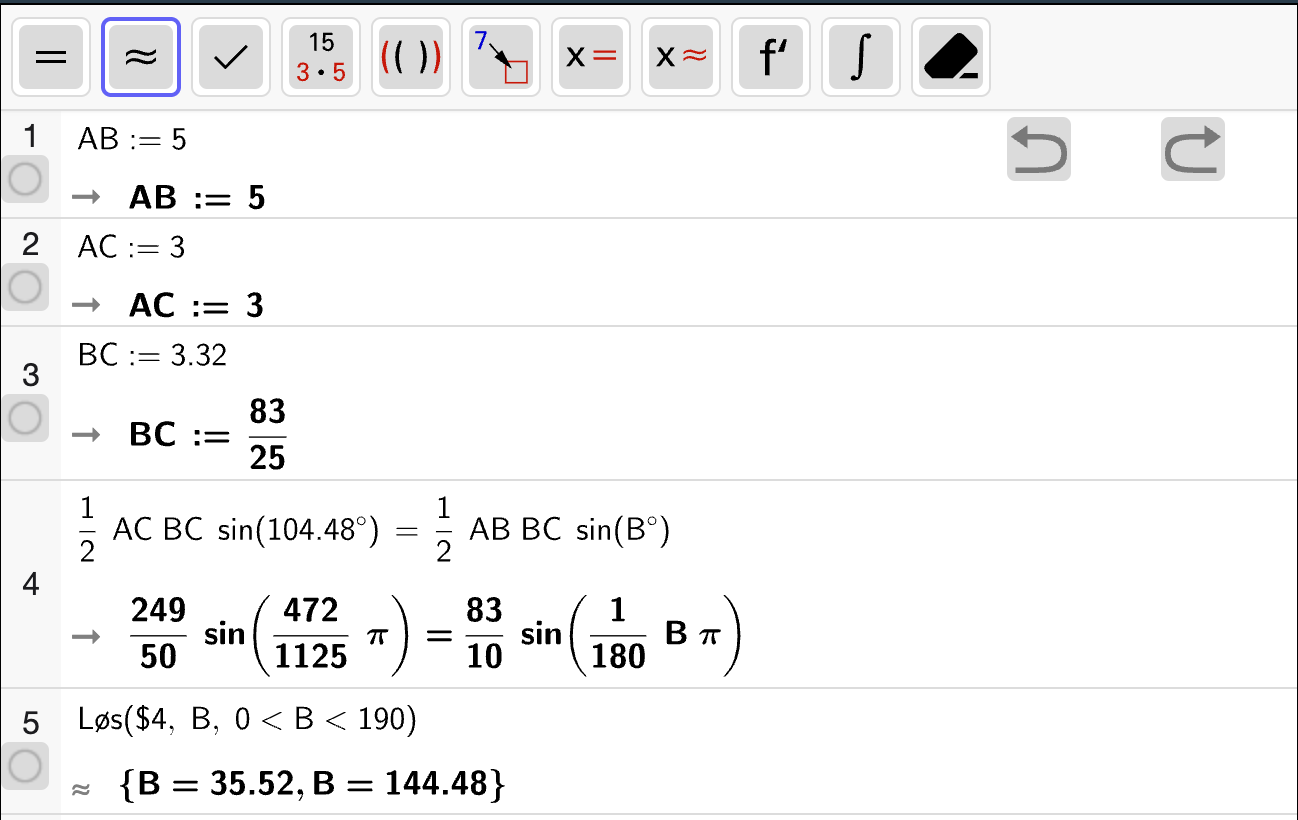
Sentralvinklene i en sirkel må summere til \(360 \degree\). Både \(\angle CSA\) og \(\angle ASB\) er toppvinkler, men ikke like som betyr at

\[\begin{align*} 2 \angle CSA + 2 \angle ASB &= 360 \degree \\ \\ \angle CSA + \angle ASB &= 180 \degree \\ \\ 135 \degree + \angle ASB &= 180 \degree \\ \\ \angle ASB &= 45 \degree \end{align*}\]

Videre er sidene som spenner ut \(\angle ASB\) gitt ved \(SA = SB = 2\) siden både \(A\) og \(B\) ligger på sirkelperiferien. Dermed kan vi bruke arealsetningen til å finne arealet av \(\triangle SAB\):

\[ T_{\triangle SAB} = \dfrac{1}{2} \cdot SA \cdot SB \cdot \sin(45 \degree). \]

Vi regner ut svaret med CAS:

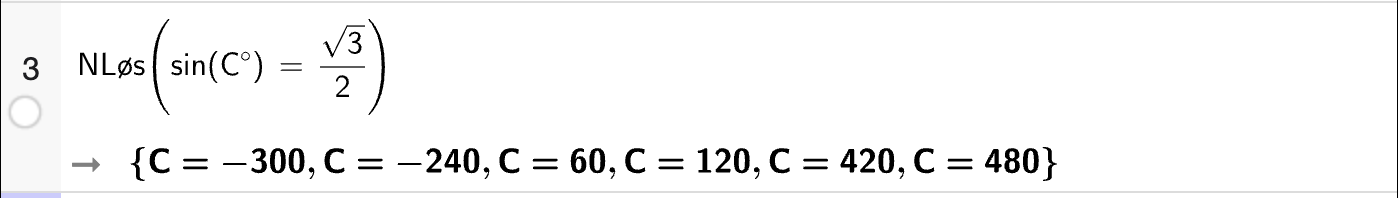
Altså er arealet av \(\triangle SAB\) gitt ved \(T_{\triangle SAB} = \sqrt{2}\). Arealet av \(\triangle CAB\) summen av arealene til de trekantene som gir

\[ T_{\triangle CAB} = T_{\triangle CAS} + T_{\triangle SAB} = \sqrt{2} + \sqrt{2} = 2\sqrt{2}. \]

---

Oppgave 8

En regulær \(n\)-kant er en \(n\)-kant hvor alle sider og vinkler er like store.

I figuren nedenfor vises en regulær \(6\)-kant som er innskrevet i en sirkel med radius \(6\). En trekant er tegnet inn der det éne hjørnet er i sentrum av sirkelen og de to andre hjørnene er på sirkelen.

Åpne CAS‑vindu

a

Bestem en eksakt verdi for arealet av trekanten.

Fasit

\[ T_\triangle = 9\sqrt{3} \]

b

Bestem en eksakt verdi for arealet av 6-kanten.

Fasit

\[ T_{6-\mathrm{kant}} = 54\sqrt{3} \]

---

Oppgave 9

I figuren nedenfor vises en regulær \(12\)-kant som innskrevet i en sirkel med radius \(r\).

Åpne CAS‑vindu

a

Bestem en eksakt verdi for arealet av \(12\)-kanten uttrykt ved \(r\).

Fasit

Arealet av \(12\)-kanten er

\[ T = 3r^2 \]

b

Bestem en formel for arealet av en regulær \(n\)-kant som er innskrevet i en sirkel med radius \(r\).

Fasit

\[ T = \dfrac{n}{2} \cdot r^2 \cdot \sin \left( \dfrac{360\degree}{n} \right) \]

c

Bruk formelen fra b til å bestemme arealet til en \(4096\)-kant.

Stemmer svaret ditt overens med det du forventer?

Fasit

\[ T \approx 3.14 r^2 \]

Løsning

Vi bruker CAS til å regne ut arealet av den regulære \(4096\)-kanten:

Altså er arealet av en regulær \(4096\)-kant som er innskrevet i en sirkel med radius \(r\) ca.

\[ T \approx 3.14 r^2 \]

som stemmer godt overens med at arealet bør være ganske nærme arealet av en sirkel med radius \(r\).