Oppgaver: Cosinussetningen

Oppgaver: Cosinussetningen#

Oppgave 1

a

Bestem $x$ i trekanten nedenfor.

Fasit

\[ x \approx 4.14 \]

Løsning

\[ x \approx 4.14 \]

b

Bestem $x$ i trekanten nedenfor.

Fasit

\[ x \approx 3.99 \]

Løsning

\[ x \approx 3.99 \]

c

Bestem $x$ i trekanten nedenfor.

Fasit

\[ x \approx 2.99 \]

Løsning

$AB < AC = 5$ som betyr at $AB \approx 5.59$ ikke er en mulighet. Dermed har vi at

\[ x \approx 2.99 \]

Oppgave 2

a

Bestem $x$ i trekanten nedenfor.

Fasit

\[ x \approx 117.28\degree \]

Løsning

\[ x \approx 117.28\degree \]

b

Bestem $x$ i trekanten nedenfor.

Fasit

\[ x \approx 104.48\degree \]

Løsning

\[ x \approx 104.48\degree \]

c

Bestem $x$ i trekanten nedenfor.

Fasit

\[ x \approx 58.81\degree \]

Løsning

\[ x \approx 58.81\degree \]

Oppgave 3

En trekant $\triangle ABC$ er vist nedenfor.

a

Bestem et eksakt uttrykk for arealet av trekanten uttrykkt ved $\ell$.

Fasit

\[ T = \dfrac{5}{2}\sqrt{3} \cdot \ell^2 \]

Løsning

Bruker arealsetningen og regner ut med CAS:

\[ T = \dfrac{5}{2}\sqrt{3} \cdot \ell^2 \]

b

Bestem et eksakt uttrykk for lengden $BC$ uttrykt ved $\ell$.

Fasit

\[ x = \sqrt{19} \cdot \ell \]

Løsning

La $x = BC$. Vi bruker cosinussetningen til å bestemme $x$ uttrykt ved $\ell$:

Vi antar at $\ell > 0$, som betyr at

\[ x = \sqrt{19} \cdot \ell \]

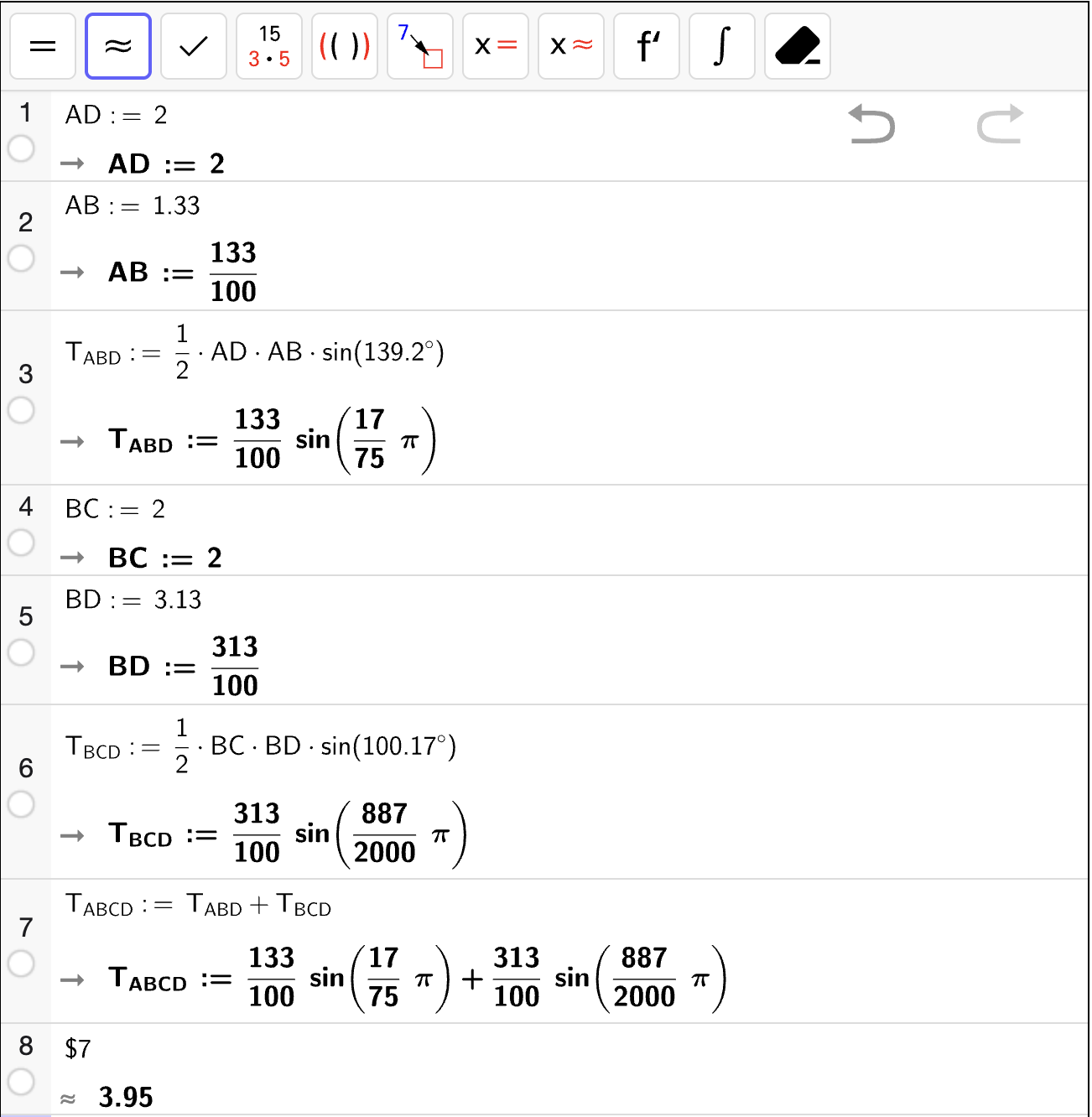
Oppgave 4

En firkant $\square ABCD$ er vist nedenfor.

a

Bestem omkretsen $\mathcal{O}$ av $\square ABCD$.

Fasit

\[ \mathcal{O} = 4 + \sqrt{3} + \sqrt{7}. \]

Løsning

Vi deler opp firkant $\square ABCD$ i to trekanter $\triangle ABC$ og $\triangle ACD$.

Først bestemmer vi lengden på diagonalen $AC$ som vi kan gjøre med Pytagoras’ setning:

\[ AC^2 = 1^2 + (\sqrt{3})^2 = 1 + 3 = 4 \limplies AC = 2 \]

Vi kan merke oss at $\triangle ABC$ er en $30\degree$-$60\degree$-$90\degree$ trekant fordi den korteste kateten er halvparten av hypotenusen. Da følger det at

\[ \angle BCA = 60\degree \limplies \angle ACD = 60\degree. \]

Da kan vi bruke cosinussetningen til å bestemme lengden $x = CD$. Vi regner det ut med CAS:

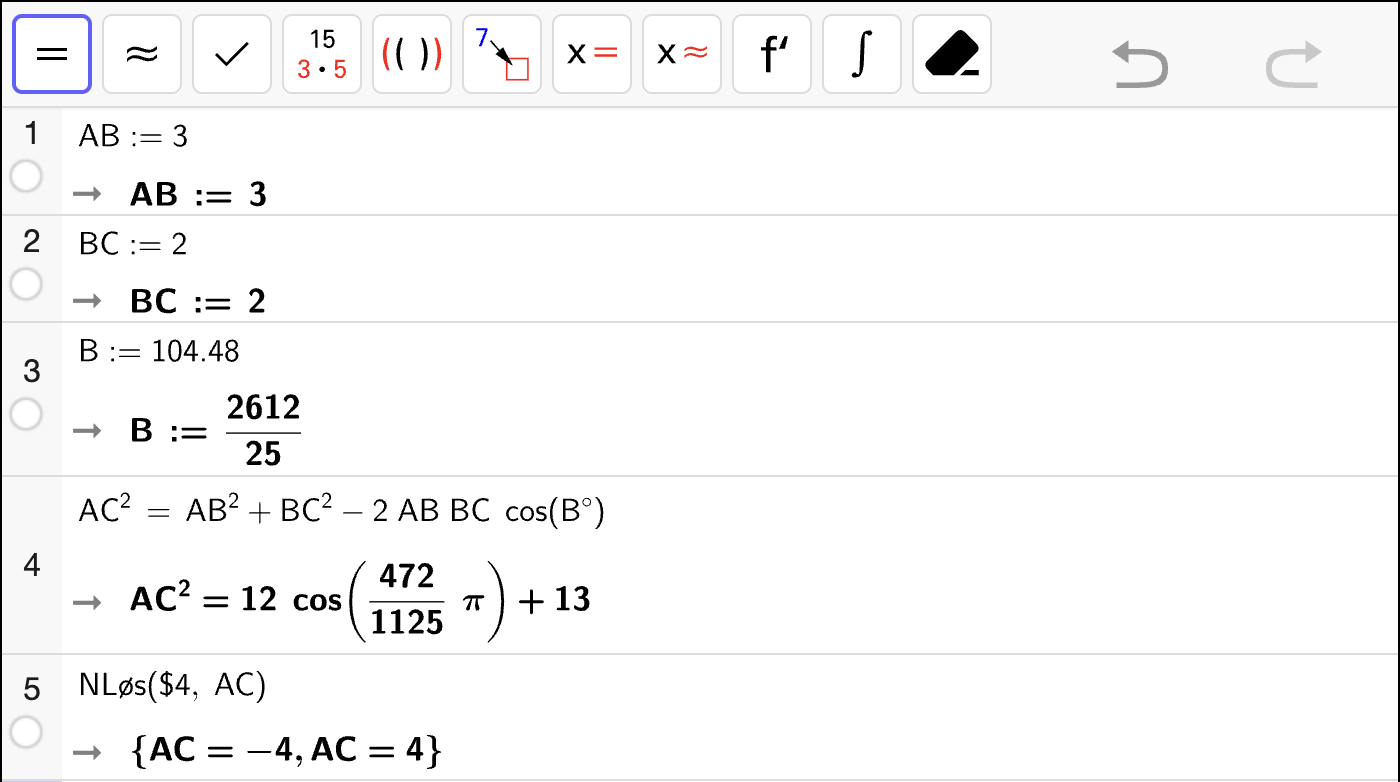
Altså er $CD = 3$. Dermed blir omkretsen til $\square ABCD$:

\[ \mathcal{O} = AB + BC + CD + DA = \sqrt{3} + 1 + 3 + \sqrt{7} = 4 + \sqrt{3} + \sqrt{7}. \]

b

Bestem arealet $T$ av $\square ABCD$.

Fasit

\[ T = 2\sqrt{3} \]

Løsning

Arealet av $\triangle ABC$ kan regnes ut direkte med grunnlinje $AB$ og høyde $BC$ (siden trekanten er rettvinklet):

\[ T_{\triangle ABC} = \dfrac{1}{2} \cdot AB \cdot BC = \dfrac{1}{2} \cdot \sqrt{3} \cdot 1 = \dfrac{\sqrt{3}}{2}. \]

For $\triangle ACD$ kan vi bruke arealsetningen ut ifra vinkel $\angle ACD$. Vi regner det ut med CAS:

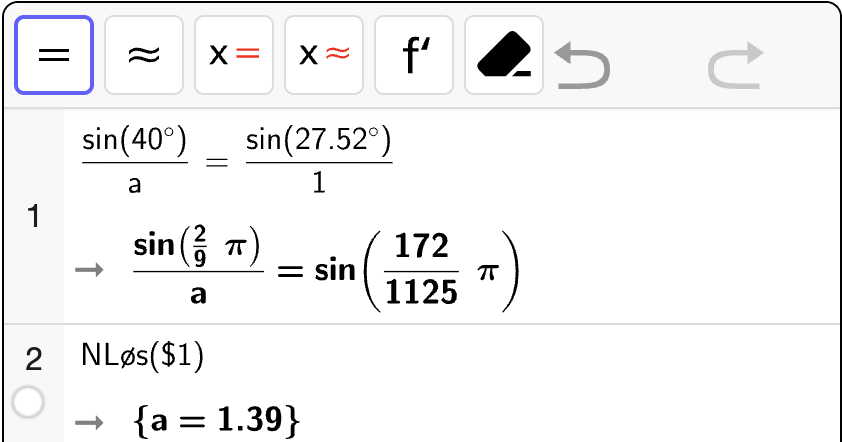
Dermed følger det at arealet av $\square ABCD$ er

\[ T = T_{\triangle ABC} + T_{\triangle ACD} = \dfrac{\sqrt{3}}{2} + \dfrac{3\sqrt{3}}{2} = 2\sqrt{3}. \]

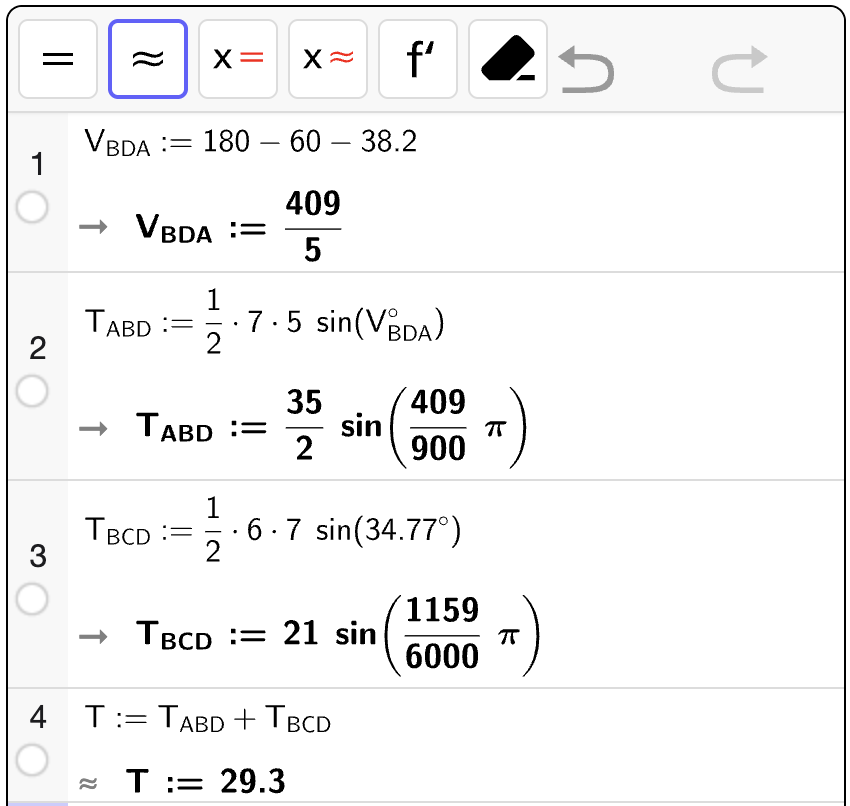
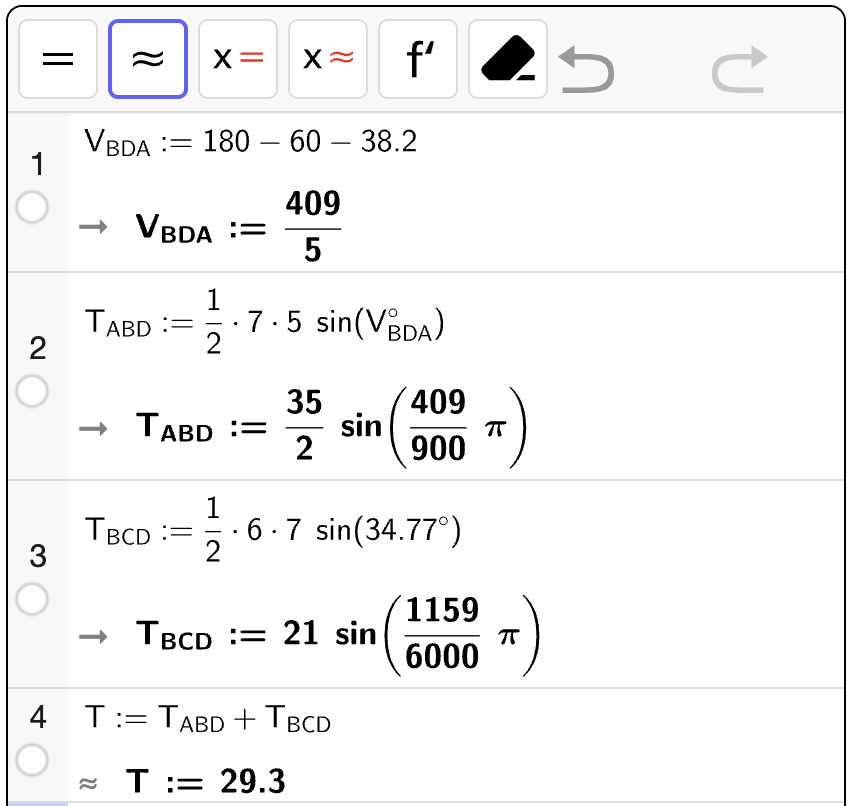
Oppgave 5

Nedenfor vises en firkant $\square ABCD$.

a

Bestem omkretsen av $\square ABCD$.

Fasit

\[ \mathcal{O} \approx 9.33. \]

Løsning

Vi bruker cosinussetningen på $\triangle BCD$ for å bestemme lengden $BD$:

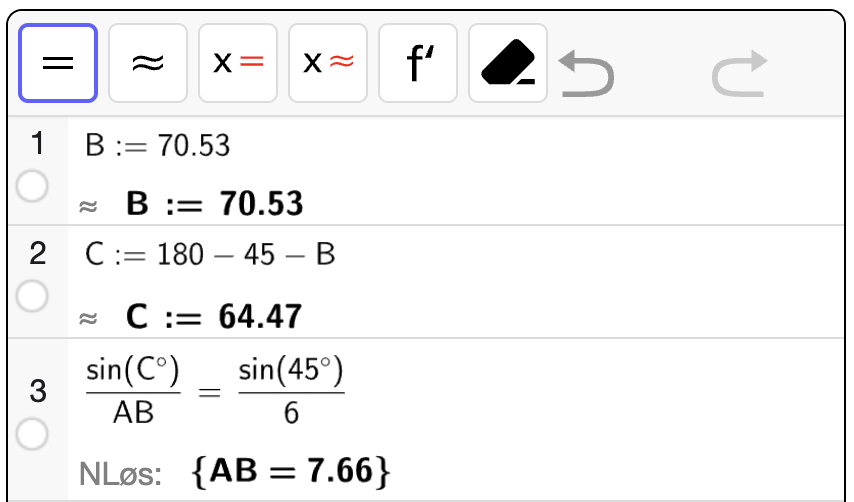
som gir

\[ BD \approx 3.13. \]

Deretter bruker vi cosinussetningen på $\triangle ABD$ for å bestemme lengden $AB$:

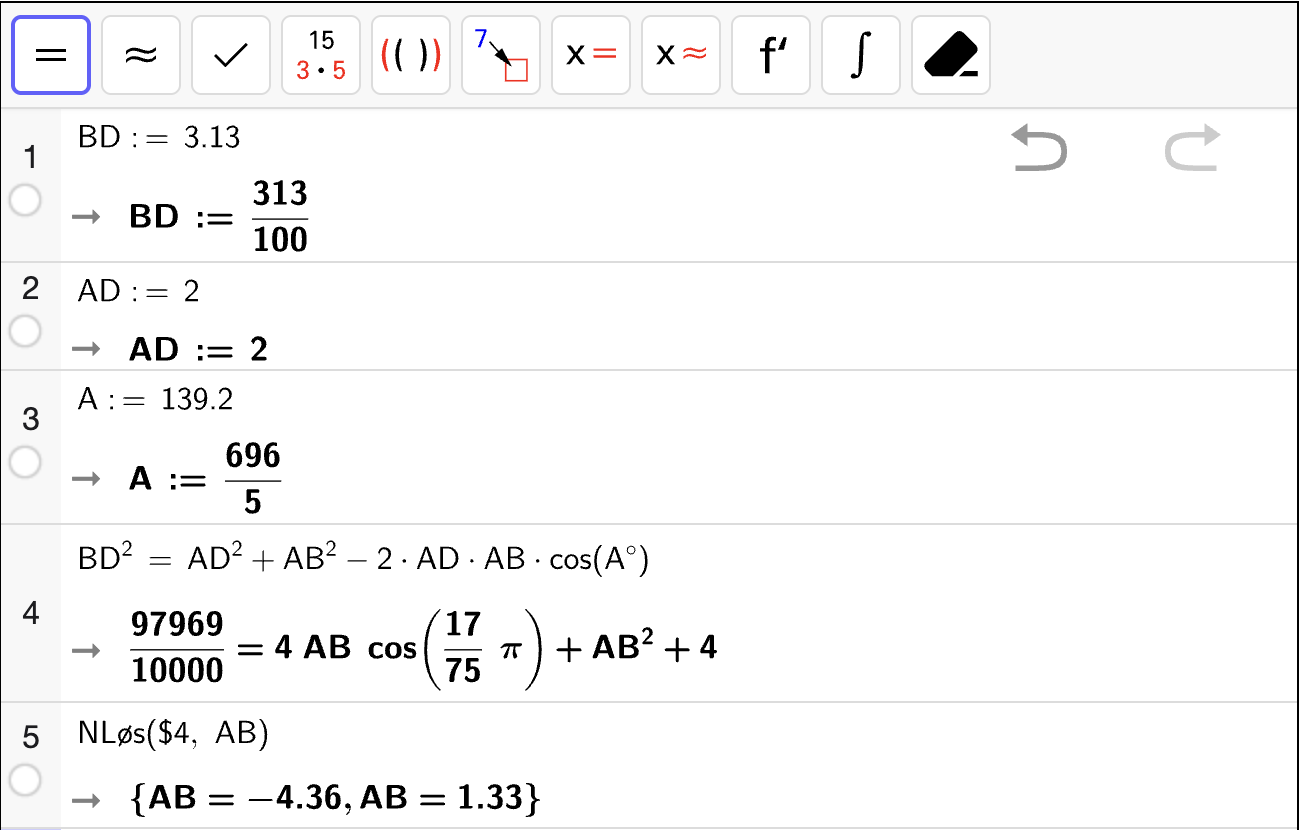
som gir

\[ AB \approx 1.33 \]

Omkretsen til $\square ABCD$ er derfor

\[ \mathcal{O} = AB + BC + CD + DA \approx 1.33 + 2 + 4 + 2 = 9.33. \]

b

Bestem arealet av $\square ABCD$.

Løsning

Fra oppgave a fant vi at

\[ AB \approx 1.33 \quad \text{og} \quad BD \approx 3.13. \]

Arealet av $\triangle ABD$ kan regnes ut med arealsetningen:

\[ T_{\triangle ABD} = \dfrac{1}{2} \cdot AB \cdot AD \cdot \sin \angle A \]

og tilsvarende for $\triangle BCD$:

\[ T_{\triangle BCD} = \dfrac{1}{2} \cdot BC \cdot BD \cdot \sin \angle CBD \]

som vi gjør med CAS:

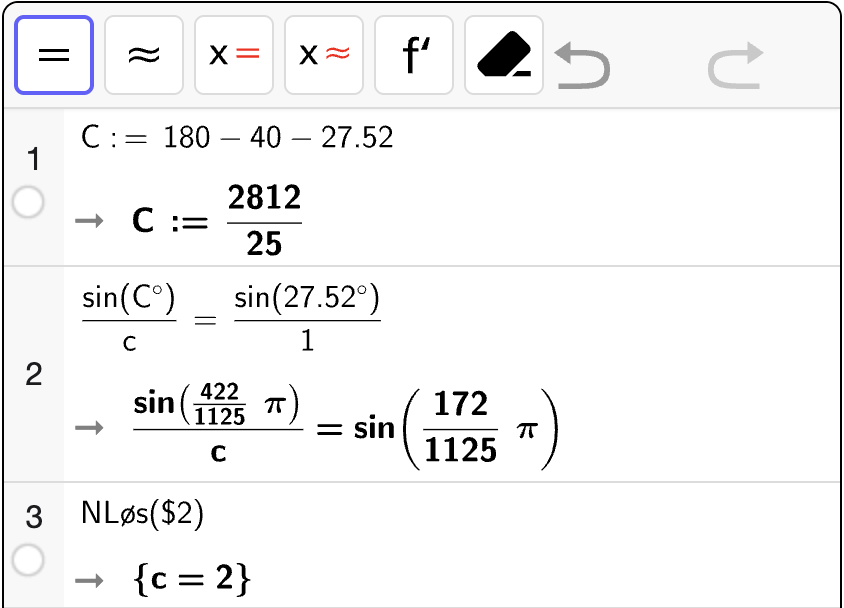
Altså er

\[ T_{\square ABCD} \approx 3.95. \]

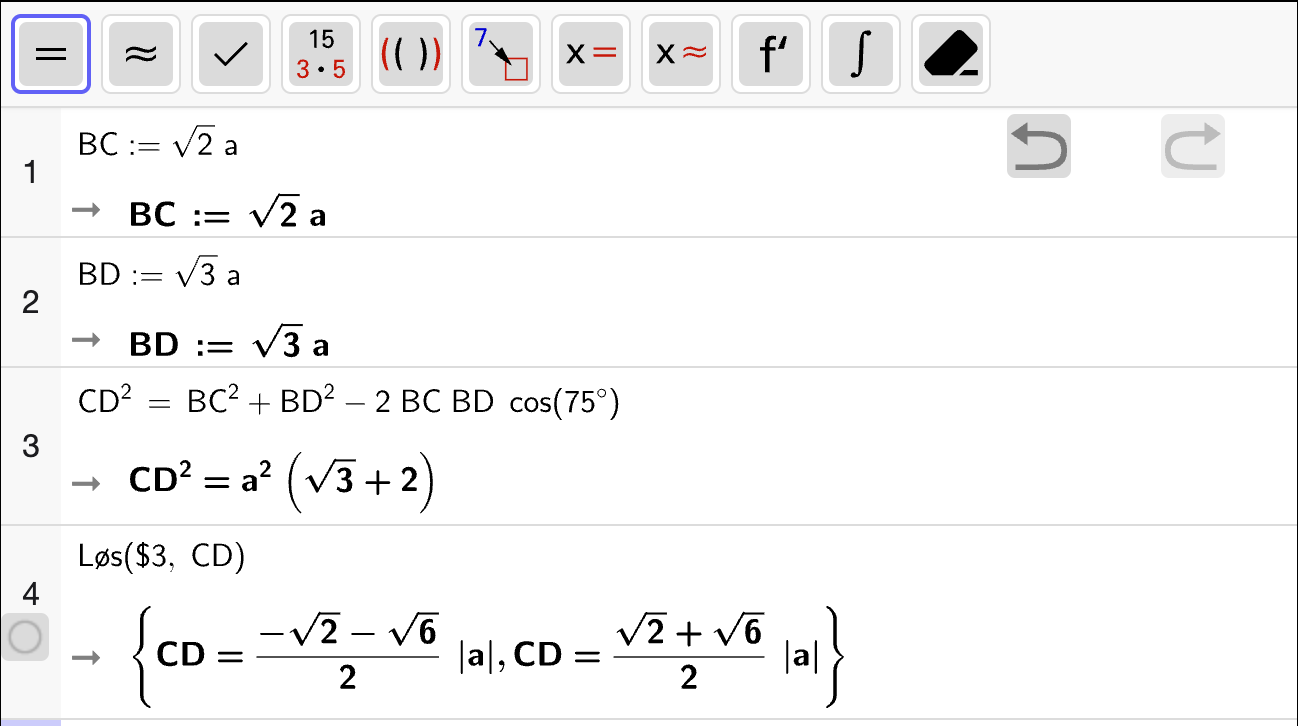
Oppgave 6

En firkant $\square ABCD$ er vist nedenfor.

a

Bestem et eksakt uttrykk for $BD$ uttrykt ved $a$.

Fasit

\[ BD = \sqrt{3} \cdot a. \]

Løsning

La $x = BD$. Vi kan merke oss at siden $\angle ADB = 30 \degree$ og $\angle A = 120\degree$, så følger det at $\angle ABD = 30\degree$ som betyr at $\triangle ABD$ er en likebeint trekant. Dermed er $AB = AD = a$. Da kan bruke cosinussetningen til å bestemme $x$:

Dermed er

\[ x = BD = \sqrt{3} \cdot a. \]

b

Bestem et eksakt uttrykk for omkretsen til $\square ABCD$.

Fasit

\[ \mathcal{O} = \dfrac{1}{2}\cdot a \cdot \left(3\sqrt{2} + \sqrt{6} + 4\right). \]

Løsning

Vi bestemmer lengden $CD$ ved å bruke cosinussetningen ut ifra vinkel $\angle DBC$ som gir

\[ CD^2 = BC^2 + BD^2 - 2 \cdot BC \cdot BD \cdot \cos(75\degree). \]

Vi gjør utregningene med CAS:

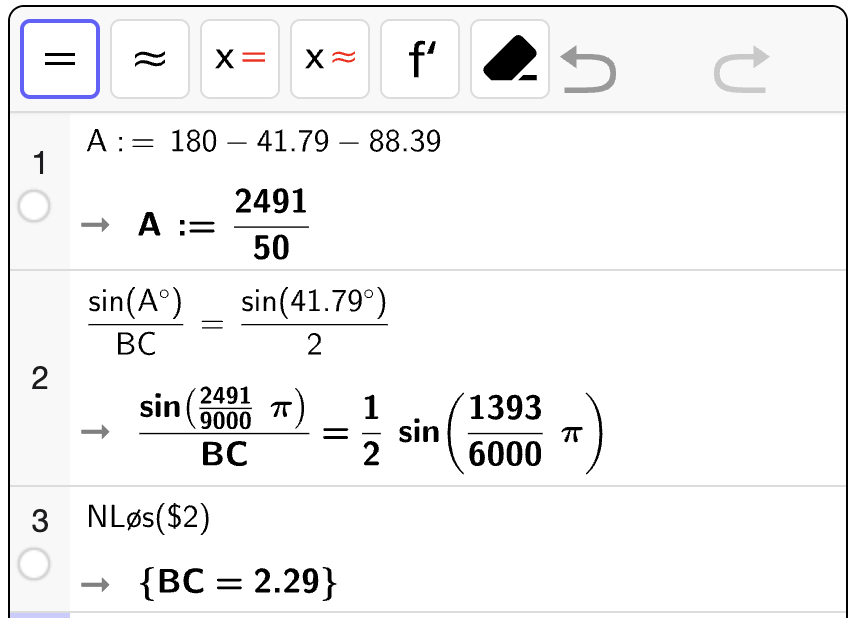
Det er bare den positive løsningen som gir mening, så vi får at

\[ CD = \dfrac{\sqrt{2} + \sqrt{6}}{2} \cdot a \]

der $a = |a|$ siden $a$ er positiv. Nå kjenner vi alle sidelenger i $\square ABCD$ og kan regne ut omkretsen:

\[ \mathcal{O} = AB + BC + CD + DA \]

vi gjør selve utregningen med CAS:

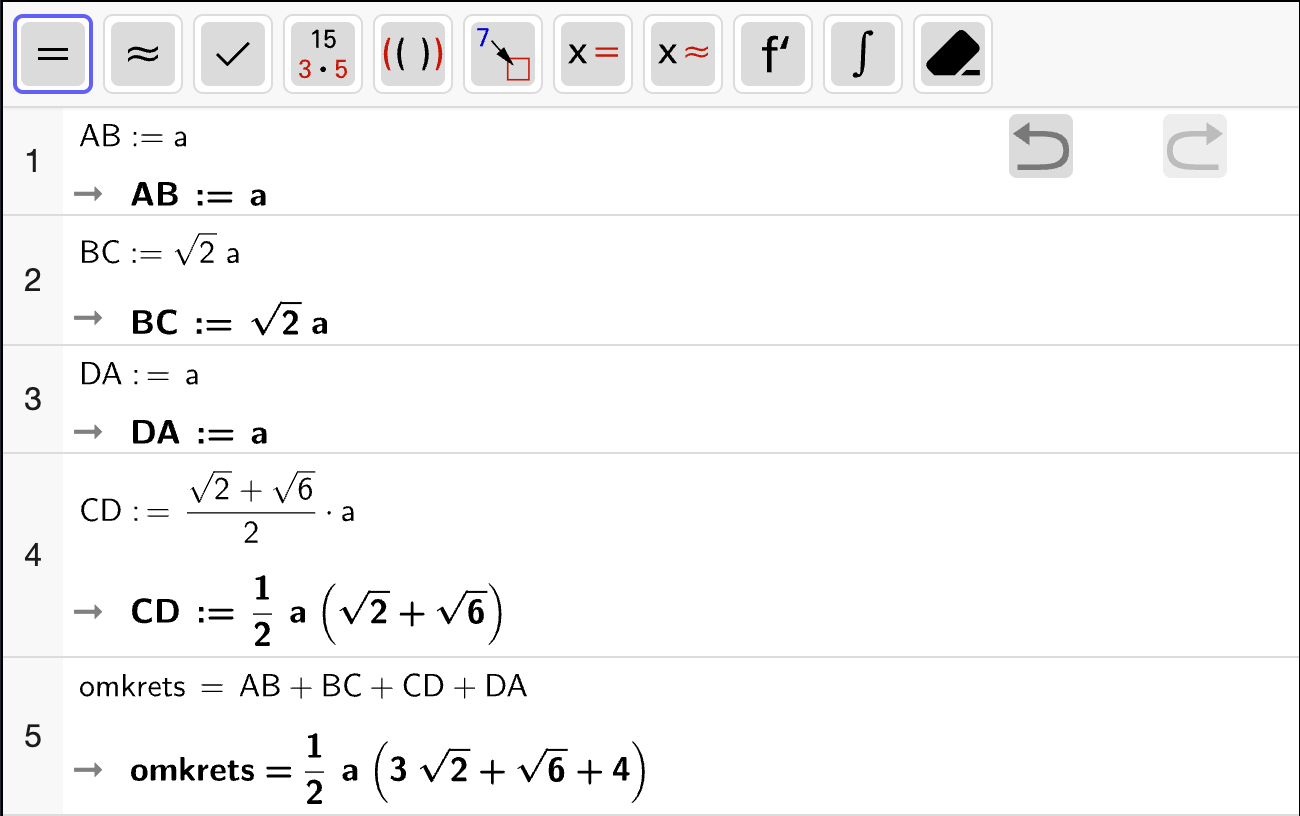
Altså er omkretsen til $\square ABCD$:

\[ \mathcal{O} = \dfrac{1}{2}\cdot a \cdot \left(3\sqrt{2} + \sqrt{6} + 4\right). \]

c

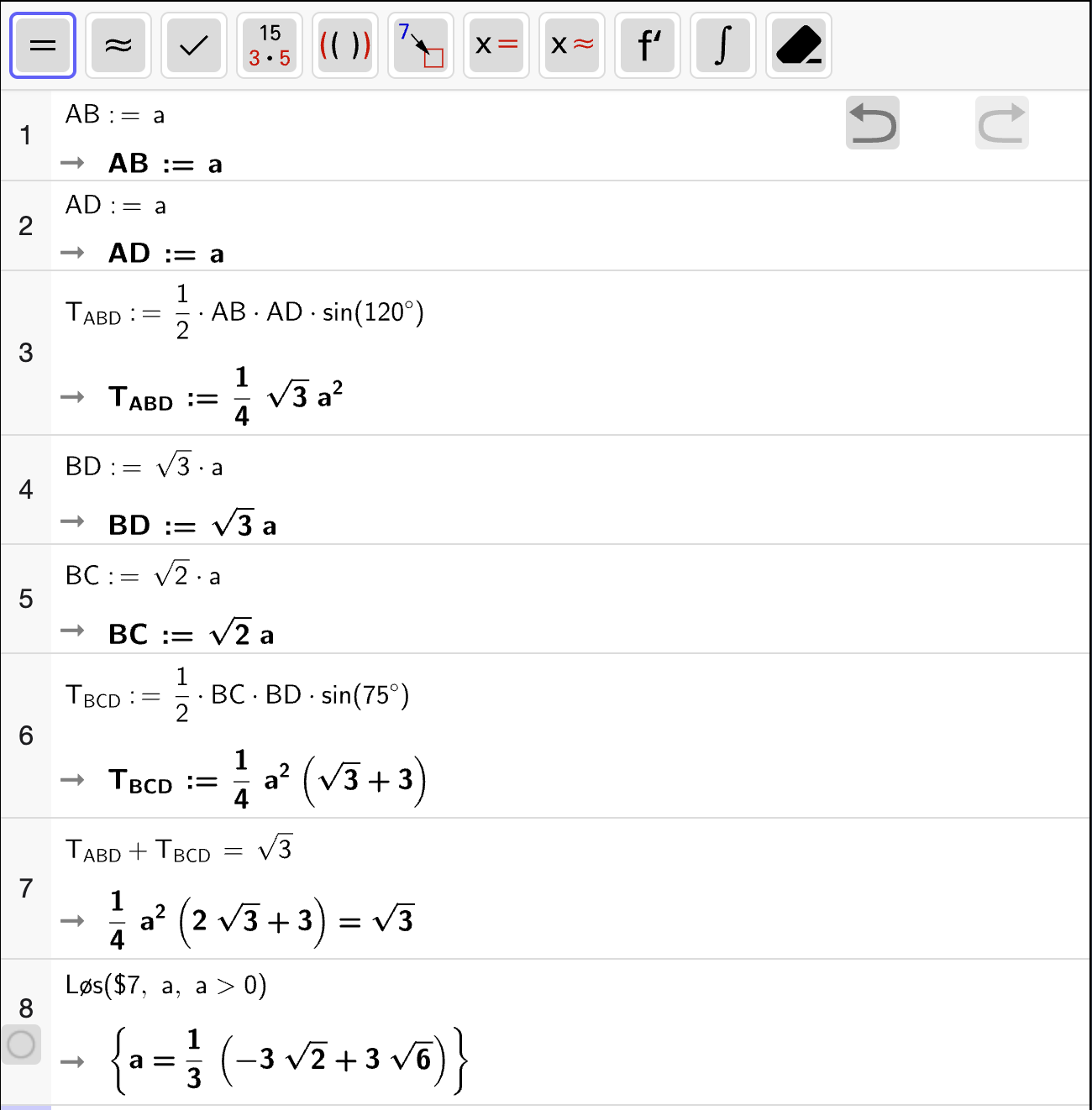
Bestem $a$ slik at arealet av firkanten er $\sqrt{3}$.

Fasit

\[ a = \sqrt{6} - \sqrt{2} \]

Løsning

Vi setter opp en likning der vi uttrykket arealet til $\square ABCD$ ved $a$ ved å bruke arealsetningen på $\triangle ABD$ og $\triangle BCD$, som vi løser med CAS:

Altså er arealet av $\square ABCD$ lik $\sqrt{3}$ dersom

\[ a = \sqrt{6} - \sqrt{2} \]

Oppgave 7

Nedenfor vises en regulær 5-kant $ABCDE$. Alle sidelengdene er $\ell$ og vinklene i hvert hjørne er $108 \degree$.

a

Bestem et eksakt uttrykk for $AC$ uttrykt ved $\ell$.

Fasit

\[ AC = \dfrac{1}{2}\left(\sqrt{5} + 1\right)\cdot \ell \]

Løsning

Vi bruker cosinussetningen med $AB = BC = \ell$ som gir:

\[ AC = \dfrac{1}{2}\left(\sqrt{5} + 1\right)\cdot \ell \]

b

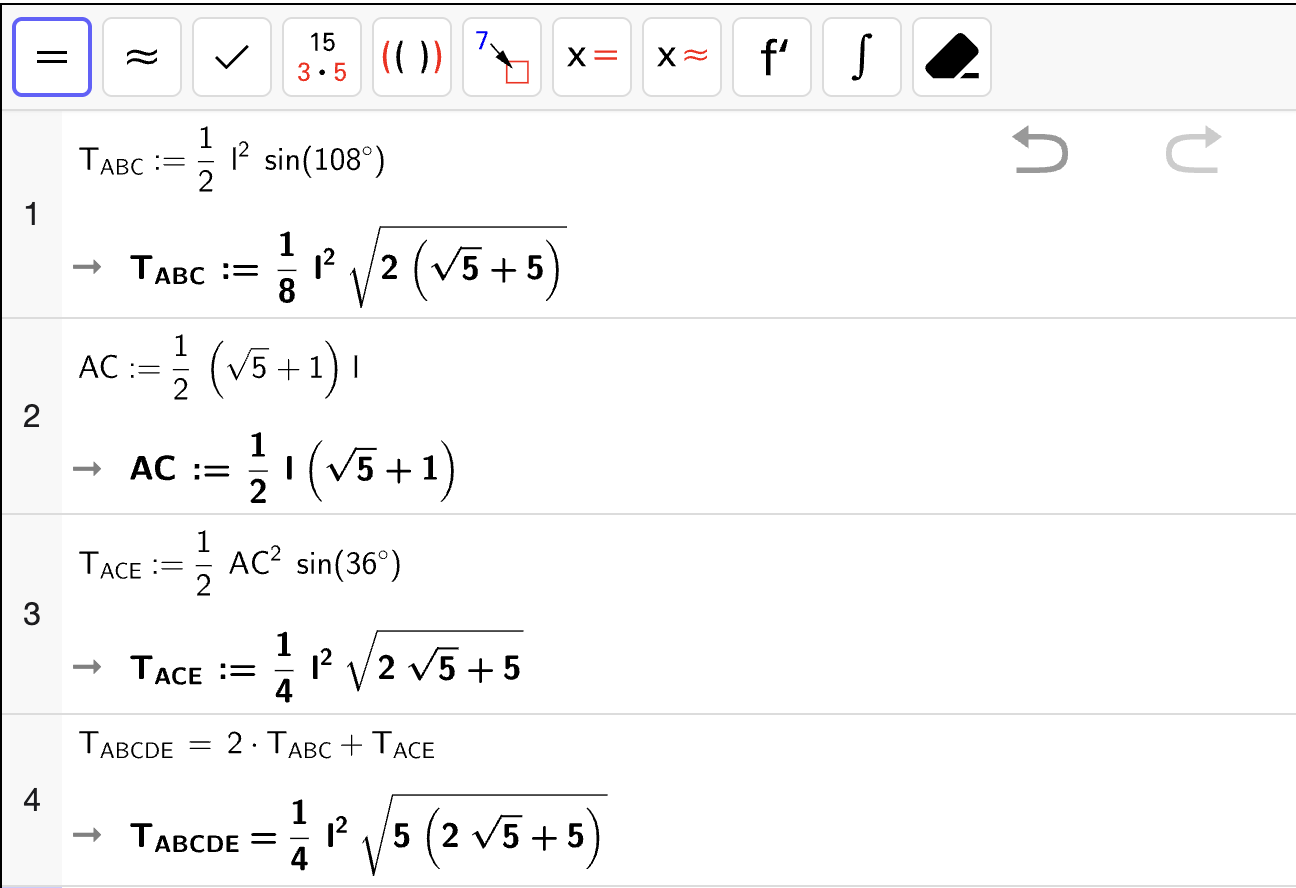
Bestem et eksakt uttrykk for arealet av 5-kanten uttrykt ved $\ell$.

Fasit

\[ T_{ABCDE} = \dfrac{1}{4} \sqrt{5\left(2\sqrt{5} + 5\right)} \cdot \ell^2 \]

Løsning

Fra figuren, kan vi merke oss at 5-kant $ABCDE$ er delt opp i tre trekanter $\triangle ABC$, $\triangle ACE$ og $\triangle CDE$. Vi kan også merke oss at $\triangle ABC$ og $\triangle CDE$ er kongruente (de er formlike og like store) fordi $\angle D = \angle B$ og $CD = DE = \ell$. Dermed kan vi uttrykke arealet av 5-kanten som

\[ T_{ABCDE} = T_{\triangle ABC} + T_{\triangle ACE} + T_{\triangle CDE} = 2T_{\triangle ABC} + T_{\triangle ACE}. \]

Arealet av $\triangle ABC$ kan regnes ut med arealsetningen:

\[ T_{\triangle ABC} = \dfrac{1}{2} \ell^2 \cdot \sin(108\degree). \]

I $\triangle ACE$ kan vi konkludere at $AC = CE$ ettersom de er tilsvarende sider i $\triangle ABC$ og $\triangle CDE$. Vi trenger å kjenne til vinkelen som spenner ut av sidene $AC$ og $CE$. Vi bruker en hjelpefigur for å bestemme vinkelen:

Her kan vi se at

\[ \angle C = 108\degree = \gamma + 2\alpha. \]

Men vi vet også at

\[ 2\alpha + 108\degree = 180\degree \liff 2\alpha = 72\degree \]

som betyr at

\[ 108\degree = \gamma + 2\alpha = \gamma + 72\degree \liff \gamma = 36\degree. \]

Da følger det at arealet at $\triangle ACE$ er

\[ T_{\triangle ACE} = \dfrac{1}{2} AC^2 \cdot \sin(36\degree). \]

Vi regner ut med CAS:

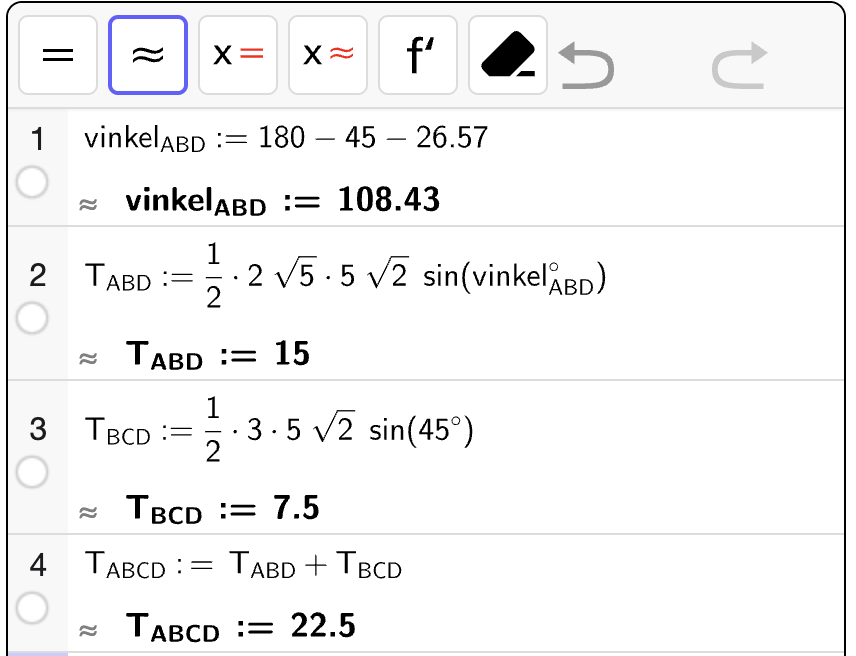
Dermed finner vi at arealet av $5$-kanten er

\[ T_{ABCDE} = \dfrac{1}{4} \sqrt{5\left(2\sqrt{5} + 5\right)} \cdot \ell^2 \]

Oppgave 8

Anna jobber med å finne en ukjent side $x$ i trekant.
Hun har brukt cosinussetningen og har satt opp likningen

\[ 14^2 = 16^2 + x^2 - 16x. \]

Hvilke opplysninger kan Anna ha fått om trekanten?

Løsning

Cosinussetningen kan skrives som

\[ a^2 = b^2 + c^2 - 2\cdot b \cdot c \cdot \cos A. \]

Sammenlikner vi likningen ovenfor med likningen til Anna, kan vi se at det passer dersom

\[ a = 14 \and b = 16 \and c = x \and \cos A = \dfrac{1}{2} \]

Det betyr at

\[ A = 60 \degree. \]

Dette er en mulighet for opplysningene Anna kan ha fått.

Oppgave 9

Nedenfor vises en regulær $7$-kant med sidelengder $2$.

Bestem arealet av $7$-kanten.

Fasit

\[ T_{\mathrm{7-kant}} \approx 14.5. \]

Løsning

Vi starter med å bestemme $AC$ ved hjelp av cosinussetningen. La $L = 2$ være sidelengdene i $7$-kanten slik at $L = AB = BC$. Da kan vi bestemme $AC$ som følger:

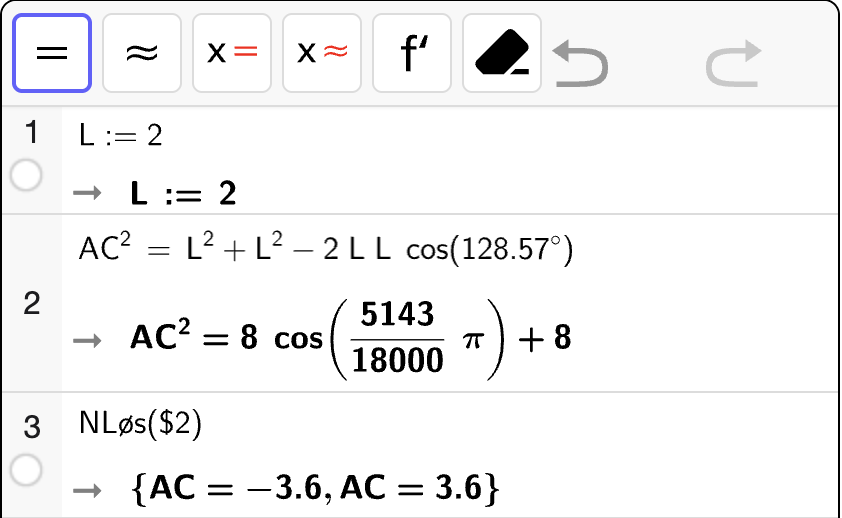
Altså er $AC \approx 3.6$.

Vi kan nå regne ut arealet til $\triangle ABC$, $\triangle CDE$ og $\triangle FGA$ siden alle disse trekantene er kongruente. Men vi trenger å bestemme noen flere lengder og vinkler for å bestemme arealet av de resterende trekantene i figuren.

La oss lage en liste med mål:

Vi må bestemme lengden $CF$ og vinkelen $\angle FAC$ for å bestemme arealet av $\triangle ACF$
Vi må bestemme lengden vinkelen $\angle FCE$ for å bestemme arealet av $\triangle CEF$

Når vi har disse størrelsene kan vi bestemme arealet av de to resterende trekantene i figuren. Vi starter med å bestemme $CF$ og $\angle CAF$. I $\triangle ACF$ vet vi allerede at

\[ AC = AF = 3.6 \]

Vi må for å kunne bruke cosinussetningen, må vi bestemme vinkelen $\angle FAC$ først. Først kan vi observere at $\angle CAB = \angle BCA$ og

\[ \angle CAB + \angle BCA + 128.57 \degree = 180 \degree \liff 2\cdot \angle CAB = 180 \degree - 128.57 \degree \]

som betyr at

\[ \angle CAB = 25.71 \degree. \]

Videre kan vi observere at $\angle CAB = \angle GAF$ siden $\triangle ABC \cong \triangle FGA$. Trekantene er kongruente. Dermed følger det at

\[\begin{align*} \angle CAB + \angle GAF + \angle FAC &= 128.57\degree \\ \\ 2\cdot \angle CAB + \angle FAC &= 128.57\degree \\ \\ \angle FAC &= 128.57\degree - 2\cdot \angle CAB \\ \\ \angle FAC &= 128.57\degree - 2\cdot 25.71\degree \\ \\ \angle FAC &= 77.14\degree. \end{align*}\]

Nå har vi opplysningene vi trenger for å bestemme sidelengden $CF$ med cosinussetningen:

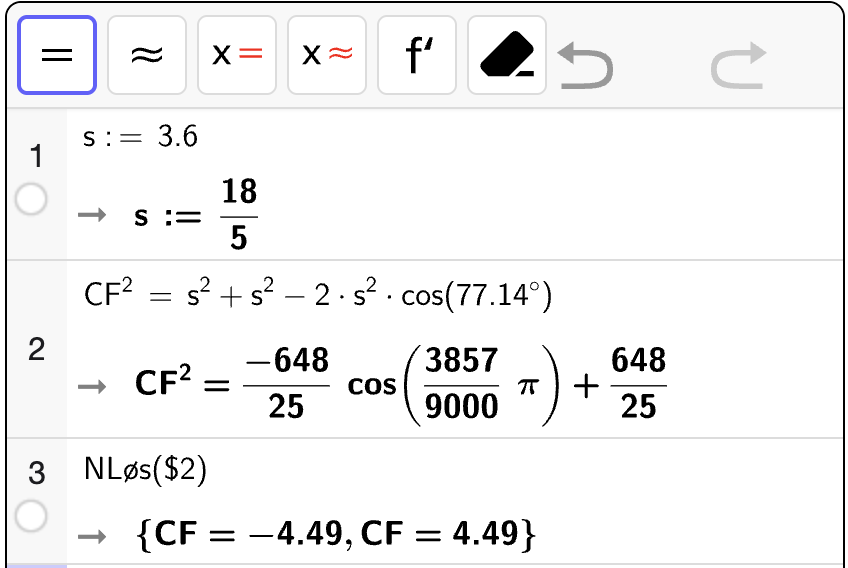
Altså er $CF \approx 4.49$. Da har vi alle opplysninger vi trenger for å bestemme arealet av $\triangle ACF$.

Vi går nå videre til å bestemme $\angle CEF$ for å kunne bestemme arealet av $\triangle CEF$. Siden $\triangle ABC \cong \triangle CEF$, så følger det at

\[ \angle DEF = \angle CAB = 25.71\degree. \]

så vi har

\[ \angle DEF + \angle CEF = 128.57 \degree \liff \angle CEF = 128.57\degree - 25.71\degree \]

som betyr at

\[ \angle DEF = 102.86\degree. \]

Nå har vi alle opplysninger vi trenger for å bestemme arealet av alle trekantene i figuren. Vi bruker arealsetningen til å bestemme arealet av hver trekant:

\[\begin{align*} T_{\text{7-kant}} &= \underbrace{T_{\triangle ABC} + T_{\triangle CDE} + T_{\triangle FGA}}_{\displaystyle 3 \cdot T_{\triangle ABC}} + T_{\triangle ACF} + T_{\triangle CEF} \\ \\ &= 3\cdot T_{\triangle ABC} + T_{\triangle ACF} + T_{\triangle CEF} \end{align*}\]

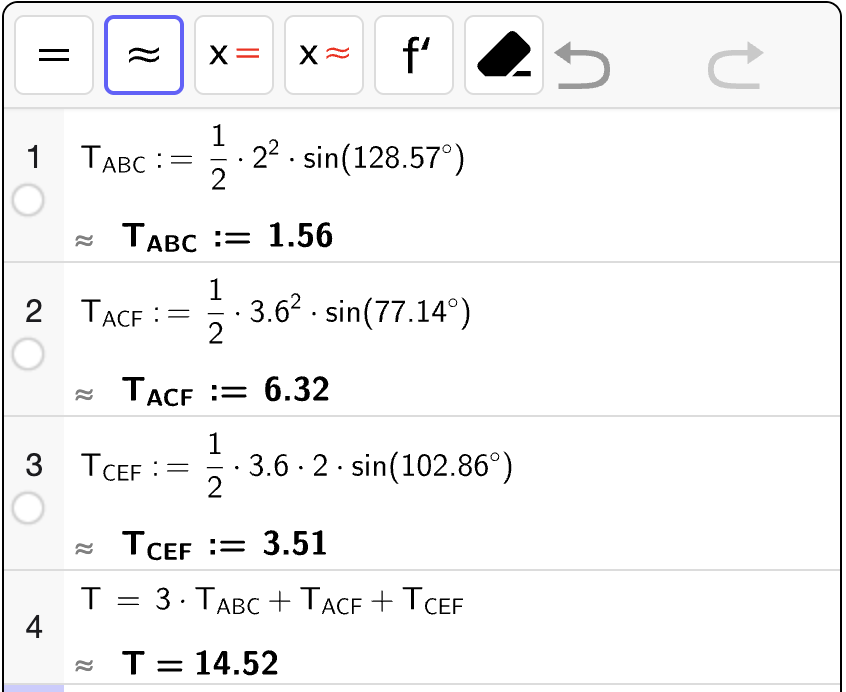
Altså er arealet av $7$-kanten

\[ T_{\mathrm{7-kant}} \approx 14.5. \]