19. Vekstfart#
Læringsmål
Kunne bestemme gjennomsnittlig vekstfart til en funksjon.
Kunne bestemme den momentane vekstfarten til en funksjon.
Kunne bestemme den deriverte til en andregradsfunksjon og bruke den til å finne egenskaper ved funksjonen.
Når vi jobbet med lineære funksjoner, så var en sentral egenskap at de har et stigningstall. Stigningstallet forteller oss hvor mye funksjonsverdier endrer seg når vi endrer \(x\)-verdien med én enhet. Mer generelt kaller vi dette for en funksjon sin vekstfart. Målet vårt her er å definere meningsfulle måter å måle hvor mye funksjonsverdien til en andregradsfunksjon endrer seg når vi endrer på \(x\)-verdien.
Gjennomsnittlig vekstfart#
Gjennomsnittlig vekstfart er et mål på hvor mye funksjonsverdien endrer seg i gjennomsnitt i et intervall dersom vi øker \(x\) med én enhet. Vi kan tolke dette som stigningstallet til en rett linje som går gjennom to punkter på grafen til funksjonen.
Gjennomsnittlig vekstfart
Den gjennomsnittlige vekstfarten til en andregradsfunksjon \(f\) i intervallet \([a, b]\) er gitt ved
Se figuren nedenfor. Linja som går gjennom de to punktene kaller vi for en sekant. Den gjennomsnittlige vekstfarten er altså stigningstallet til sekanten.
La oss se på et eksempel:
Eksempel 1
Nedenfor vises grafen til en andregradsfunksjon \(f\).
Bestem den gjennomsnittlige vekstfarten til \(f\) i intervallet \([1, 3]\).
Løsning
Fra grafen til \(f\) ser vi at \(f(1) = -4\) og \(f(3) = 0\). Den gjennomsnittlige vekstfarten i intervallet \([1, 3]\) er da gitt ved
Altså øker funksjonsverdien til \(f\) i gjennomsnitt med \(2\) når vi øker \(x\) med \(1\) i intervallet \([1, 3]\).
Underveisoppgave 1
En andregradsfunksjon \(f\) er vist i figuren nedenfor.
Bestem den gjennomsnittlige vekstfarten til \(f\) i intervallet \([-2, 1]\).
Fasit
Løsning
Vi ser fra grafen til \(f\) at \(f(-2) = 3\) og \(f(1) = 0\). Den gjennomsnittlige vekstfarten i intervallet \([-2, 1]\) er da gitt ved
Momentan vekstfart#
Momentan vekstfart er et mål på hvor mye funksjonsverdien endrer seg når vi øker \(x\) med en veldig liten verdi. Vi kan tolke det som et mål på hvor bratt grafen er i et punkt. Vi skal se på momentan vekstfart som stigningstallet til en lineær funksjon som vi kaller for en tangent.
Momentan vekstfart
Den momentane vekstfarten til en andregradsfunksjon \(f\) i \(x = a\), er gitt ved stigningstallet til en linje som berører grafen til \(f\) i punktet \((a, f(a))\). Denne linjen kaller vi for en tangent.
Vi definerer en ny skrivemåte for den momentane vekstfarten:
Se figuren nedenfor.
Det er ikke opplagt hvordan vi kan finne stigningstallet til en tangent, siden det er en linje der vi bare vet om ett punkt på linja. Vi skal snart se hvordan vi kan gjøre dette med regning, men det er hensiktsmessig å først se hvordan vi kan gjøre det med digitale verktøy. La oss se på et eksempel:
Eksempel 2
I gif-en nedenfor viser vi hvordan vi kan bestemme likningen til en tangent til grafen til en andregradsfunksjon \(f\) i punktet \((3, f(3))\). Andregradsfunksjonen er gitt ved
Likningen til tangenten i \((3, f(3))\) er
Stigningstallet til tangenten er \(2\). Den momentane vekstfarten til \(f\) i punktet \((3, f(3))\) er dette stigningstallet. Vi skriver dette som
Underveisoppgave 2
En andregradsfunksjon \(f\) er gitt ved
Bruk Geogebra-vinduet til å bestemme den momentane vekstfarten til \(f\) i punktet \((1, f(1))\).
Fasit
Løsning
Vi skriver inn funksjonsuttrykket, lager punktet og bruker Tangent(punkt, funksjon) for å finne likningen til tangenten. Se figuren nedenfor:
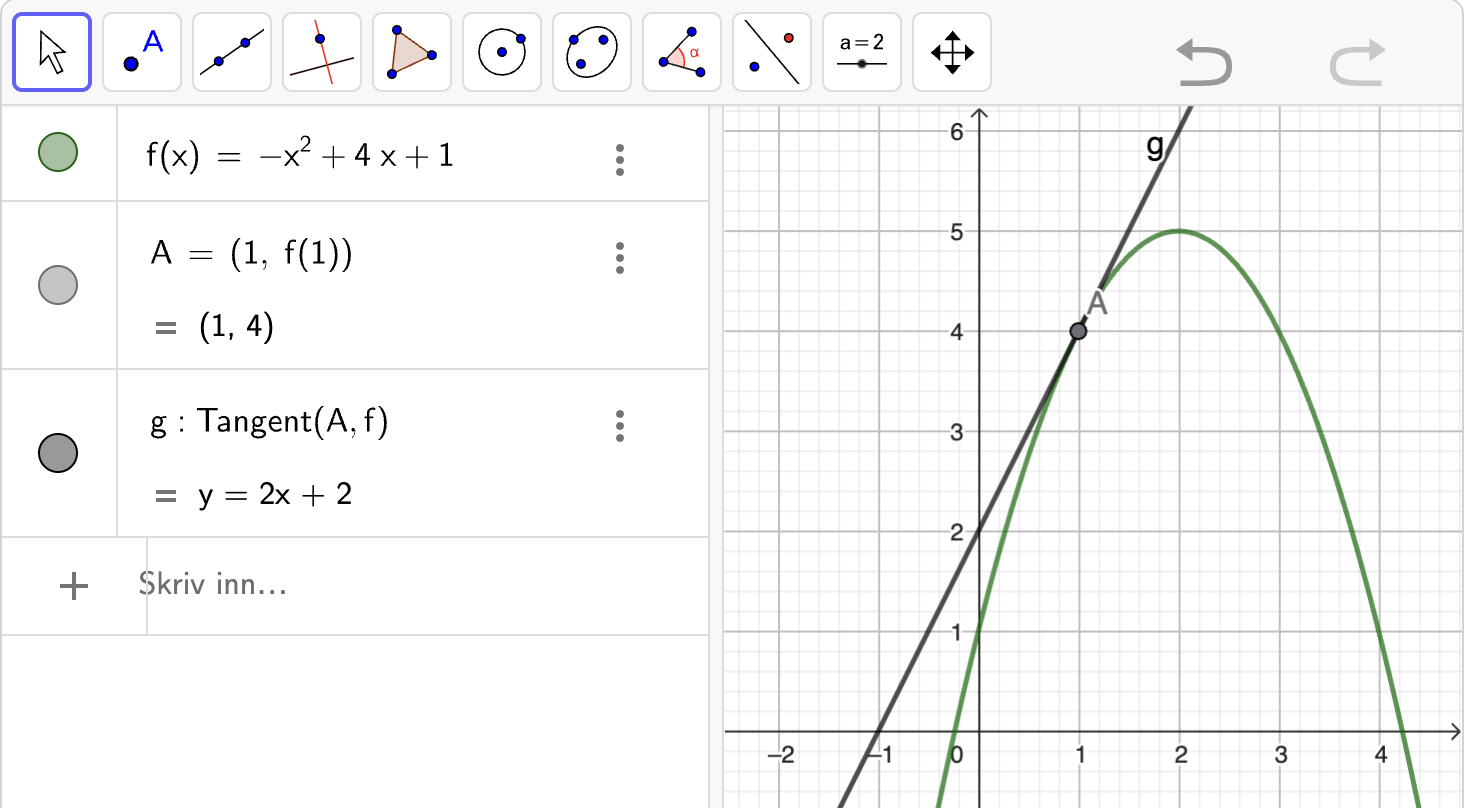
Vi ser at likningen til tangenten er
Stigningstallet til tangenten er \(2\). Den er den momentane vekstfarten til \(f\) i punktet \((1, f(1))\) er dette stigningstallet. Vi skriver dette som:
Den deriverte#
Siden vi kan bestemme stigningstallet til tangenter overalt på grafen til en andregradsfunksjon, er det naturlig å lure på om det finnes en funksjon som gir oss stigningstallet i alle punkter på grafen. Det gjør det, og denne funksjonen kaller vi for den deriverte til \(f\). Vi skriver denne funksjonen som \(f'\) og leser det som “\(f\)-derivert”.
Den deriverte
Den deriverte til en andregradsfunksjon \(f(x) = ax^2 + bx + c\) er en lineær funksjon gitt ved
Bevis
La \(f\) være en andregradsfunksjon og la \(T\) være en tangent til grafen til \(f\) i et vilkårlig punkt \((x_0, f(x_0))\). Vi kan uttrykke de to funksjonene som
der \(A\) er stigningstallet til tangenten. Siden stigningstallet til tangenten er lik den momentane vekstfarten til \(f\) i punktet \((x_0, f(x_0))\), er målet vårt å bestemme et uttrykk for \(A\). Først kan vi observere at siden tangenten bare skjærer grafen til \(f\) i ett punkt, vil likningen
bare ha én løsning. Hvis vi trekker \(T(x)\) over på venstre side, får vi en andregradsfunksjon \(f - T\) som bare skjærer \(x\)-aksen i \(x = x_0\). Dette derfor også symmetrilinja til \(f - T\). Se figuren nedenfor:
La oss utføre denne regningen:
Siden denne funksjonen har \(x = x_0\) som symmetrilinje, kan vi bruke formelen for symmetrilinja til en andregradsfunksjon:
Siden \(A\) er stigningstallet til tangenten, er det også den momentane vekstfarten til \(f\) i punktet \((x_0, f(x_0))\). Vi skriver dette som
Punktet \(x_0\) var vilkårlig, så dette vil stemme for alle punkter på grafen til \(f\). Derfor kan vi konkludere at funksjonen for den momentane vekstfarten – den deriverte – er
La oss se på et eksempel hvor vi bruker formelen:
Eksempel 3
En andregradsfunksjon \(f\) er gitt ved
Bestem \(f'(x)\).
Løsning
Den deriverte er gitt ved
Vi har at \(a = 3\) og \(b = -6\), så
Vi kan også se på en konkret sammenheng mellom \(f\) og \(f'\) dersom \(f(x)\) er skrevet på ekstremalpunktsform ved å merke oss at nullpunktet til \(f'\) ligger i symmetrilinja til \(f\). Dette stemmer fordi
Derfor må det være mulig å skrive \(f'(x)\) på nullpunktsform som
Den deriverte på nullpunktsform
Den deriverte til en andregradsfunksjon \(f(x) = a(x - x_0)^2 + y_0\) er gitt ved
Grafisk sammenheng mellom \(f\) og \(f'\)#
I animasjonen nedenfor vises sammenhengen mellom grafen til \(f\) og grafen til \(f'\). Grafen til en andregradsfunksjon \(f\) er vist til venstre og grafen til den deriverte \(f'\) er vist til høyre.
Vi kan oppsummere noen viktige observasjoner fra animasjonen:
Grafisk sammenheng mellom \(f\) og \(f'\)
Grafen til \(f\) stiger når \(f'(x) > 0\).
Grafen til \(f\) synker når \(f'(x) < 0\).
Grafen til \(f\) har et ekstremalpunkt når \(f'(x) = 0\). Symmetrilinja til \(f\) svarer til nullpunktet til den deriverte \(f'\).
La oss se på et konkret eksempel som illustrerer dette:
Eksempel 4
I figuren nedenfor vises grafen til en andregradsfunksjon \(f\) til venstre og grafen til den deriverte \(f'\) til høyre.
Fig. 19.1 grafen til \(f\) vises til venstre og grafen til \(f'\) vises til høyre.#
Vi kan legge merke til følgende:
Symmetrilinja til \(f\) er \(x = -2\). Vi kan også se at da skjærer grafen til \(f'\) gjennom \(x\)-aksen. Med andre ord er \(f'(x) = 0\) ved ekstremalpunktet til \(f\).
Til venstre for ekstremalpunktet til \(f\), så stiger grafen. Vi kan se at på det tilsvarende område, så ligger grafen til \(f'\) over \(x\)-aksen. Altså er \(f'(x) > 0\) og da stiger grafen til \(f\).
Til høyre for ekstremalpunktet til \(f\), så synker grafen. Vi kan se at på det tilsvarende område, så ligger grafen til \(f'\) under \(x\)-aksen. Altså er \(f'(x) < 0\) og da synker grafen til \(f\).
Underveisoppgave 4
Grafen til en andregradsfunksjon \(f\) er vist i figuren til høyre.
Nedenfor vises det fire grafer der én viser grafen til den deriverte \(f'\).
Hvilken graf viser grafen til \(f'\)?
Fasit
Graf A.
Løsning
Grafen til \(f\) har symmetrilinje i \(x = 2\). Det betyr at \(f'\) må skjære \(x\)-aksen i \(x = 2\) som både bare graf A og B gjør. Dermed kan vi utelukke graf C og D. Til venstre for symmetrilinja synker grafen til \(f\) så her må
Til høyre for symmetrilinja stiger grafen til \(f\) så her må
Dette stemmer for graf A, men ikke for graf B. Dermed er det graf A som viser grafen til \(f'\).
Anvendelser av den deriverte#
Den deriverte gir oss et nytt verktøy for å finne egenskapene til en andregradsfunksjon. Vi kan bruke den til å finne symmetrilinja til grafen, likningen til tangenter, og vi kan bruke den til å bestemme \(f(x)\) og \(f'(x)\) når vi har informasjon om grafen.
Bestemme ekstremalpunkt#
Vi har sett at grafen til den deriverte \(f'\) skjærer \(x\)-aksen i samme punkt som grafen til \(f\) har ekstremalpunkt. Eller sagt med andre ord, samme \(x\)-verdi som grafen til \(f\) har symmetrilinje. Vi kan se at dette stemmer ved å sette \(f'(x) = 0\) og løse likningen for \(x\):
Her har vi gode gamle formelen for symmetrilinja til en andregradsfunksjon! Det betyr at vi nå har et nytt verktøy for å finne symmetrilinja – eller \(x\)-koordinaten til ekstremalpunktet til grafen til \(f\). La oss se på et eksempel:
Eksempel 5
En andregradsfunksjon \(f\) er gitt ved
Bestem symmetrilinja til grafen til \(f\).
Løsning
Vi bestemmer \(f'(x)\) først. Vi ser at \(a = 1\) og \(b = -8\), så vi får
Deretter løser vi likningen
Altså er symmetrilinja til grafen til \(f\) gitt ved
Vi sjekker at dette stemmer overens med formelen for symmetrilinja til en andregradsfunksjon:
Det stemmer!
Underveisoppgave 5
Bruk den deriverte til å finne \(x\)-verdien til ekstremalpunktet til
Sjekk at svaret ditt stemmer overens ved å bruke formelen for symmetrilinja til en andregradsfunksjon.
Fasit
Løsning
Vi har at \(a = -2\) og \(b = 4\), så vi får
Deretter løser vi likningen
Vi sjekker at dette stemmer overens med formelen for symmetrilinja til en andregradsfunksjon:
Det stemmer!
Likningen til en tangent#
Når vi introduserte begrepet momentan vekstfart, så vi hvordan vi kan bestemme likningen til en tangent med digitale verktøy. Nå skal vi se hvordan vi kan gjøre det ved regning. Først minner vi oss på at likningen til en lineær funksjon med stigningstall \(a\) som går gjennom ett punkt \((x_0, y_0)\) er gitt ved ettpunktsformelen
Når linja er en tangent, så er stigningstallet \(a\) lik den momentane vekstfarten til \(f\) i punktet \((x_0, f(x_0))\). Det vil si at \(a = f'(x_0)\) og \(y_0 = f(x_0)\).
Likningen til en tangent
Likningen til en tangent til grafen til en andregradsfunksjon \(f\) i punktet \((x_0, f(x_0))\) er gitt ved
La oss se på et eksempel:
Eksempel 6
En andregradsfunksjon \(f\) er gitt ved
Bestem likningen til tangenten til grafen til \(f\) i punktet \((2, f(2))\).
Løsning
Likningen til tangenten er gitt ved
Vi har at \(x_0 = 2\). For å bestemme \(y\)-koordinaten til punktet, regner vi ut \(f(2)\):
For å bestemme stigningstallet \(a = f'(2)\), regner vi først ut den deriverte.
Deretter setter vi inn \(x = 2\):
Altså er stigningstallet til tangenten \(a = 1\). Da får vi at likningen til tangenten er gitt ved
Underveisoppgave 6
En andregradsfunksjon \(f\) er gitt ved
Bestem likningen til tangenten til grafen til \(f\) i punktet \((1, f(1))\).
Fasit
Løsning
Likningen til tangenten er gitt ved
Vi har at \(x_0 = 1\). For å bestemme \(y\)-koordinaten til punktet, regner vi ut \(f(1)\):
For å bestemme stigningstallet \(a = f'(1)\), regner vi først ut den deriverte.
Deretter setter vi inn \(x = 1\):
Da får vi at likningen til tangenten er gitt ved
Bestemme \(f(x)\) og \(f'(x)\)#
Vi kan bruke opplysninger om grafen til \(f\) og grafen til \(f'\) til å bestemme funksjonsuttrykkene \(f(x)\) og \(f'(x)\). La oss se på et eksempel:
Eksempel 7
I figuren nedenfor vises grafen til en andregradsfunksjon \(f\). Grafen har en tangent i punktet \((3, f(3))\) med likningen \(y = -4x + 13\).
Bestem \(f(x)\) og \(f'(x)\).
Løsning
Her bruker vi CAS til å sette opp et likningssystem for å bestemme \(f(x)\) og \(f'(x)\). Bruk CAS-vinduet til å utføre utregningene som vises nedenfor!
Vi skriver \(f(x)\) på standardform:
Vi ser at grafen til \(f\) skjærer \(y\)-aksen i \((0, 4)\) som betyr at \(f(0) = 4\).
Likningen til tangenten er gitt ved \(y = -4x + 13\). Siden tangenten går gjennom punktet \((3, f(3))\), kan vi bestemme \(f(3)\) ved å sette inn \(x = 3\) i likningen til tangenten:
Stigningstallet til tangenten er \(-4\), som betyr at \(f'(3) = -4\) siden stigningstallet til tangenten er lik den momentane vekstfarten til \(f\) i punktet \((3, f(3))\). Da har vi tre likninger:
Vi løser likningsssystemet med CAS for å bestemme \(a\), \(b\) og \(c\):

Vi skriver
f'(x)for å få den deriverte til \(f\) i CAS-vinduet.
Fra utskriften ser vi at
Det betyr at
og
Underveisoppgave 7
I figuren nedenfor vises grafen til en andregradsfunksjon \(f\).
Grafen har en tangent i punktet \((-2, f(-2))\) med stigningstall \(2\) og en tangent som går gjennom ett av nullpunktene til \(f\) med likningen \(y = -4x + 4\).
Bestem \(f(x)\) og \(f'(x)\).
Fasit
Løsning
Vi starter med tangenten som går gjennom punktet \((-2, f(-2))\). Siden stigningstallet er \(2\), så betyr det at den deriverte er lik denne verdien i \(x = -2\). Altså er \(f'(-2) = 2\).
Den andre tangenten går gjennom den ene nullpunktet til \(f\). Vi kan bestemme nullpunktet ved å sette likningen til tangenten lik null:
Da vet vi at ett av nullpunktene til \(f\) er \(x = 1\) og da må \(f(1) = 0\).
Stigningstallet til den samme tangenten er \(-4\) så da må \(f'(1) = -4\). Da har vi tre likninger:
Da kan vi bruke CAS til å løse likningssystemet:

Fra utskriften ser vi at
Det betyr at
