Oppgaver: Lineære likninger#
Oppgave 1
I figuren nedenfor vises grafen til \(f(x) = x + 3\).
Bruk figuren til å løse likningen
Fasit
Bruk figuren til å løse likningen
Fasit
Bruk figuren til å løse likningen
Fasit
Bruk figuren til å løse likningen
Fasit
Oppgave 2
Løs likningene grafisk med graftegneren i Geogebra.
Hvordan løser jeg likningen grafisk med Geogebra?
En likning er gitt ved
Nedenfor ser du en gif som viser hvordan man løser likningen med grafvinduet i Geogebra. Vi trykker på (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktet.
Skjæringspunktet er \((-1, -4)\). Det er \(x\)-koordinaten som er løsningen av likningen, så løsningen er
Fasit
Løsning
Vi skriver uttrykkene til venstre og høyre side i algebrafeltet og trykker på (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktet. Se figuren nedenfor.
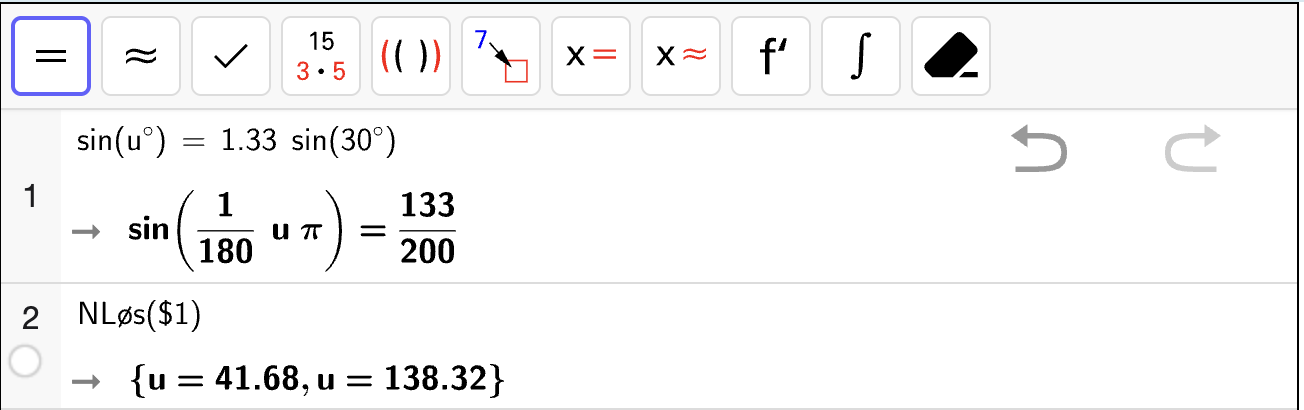
Vi ser at skjæringspunktet er \((3, 1)\). Det er \(x\)-koordinaten som er løsningen av likningen, så løsningen er
Fasit
Løsning
Vi skriver inn uttrykkene på venstre og høyre side av likningen i algebrafeltet og trykker på (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktene. Se figuren nedenfor.
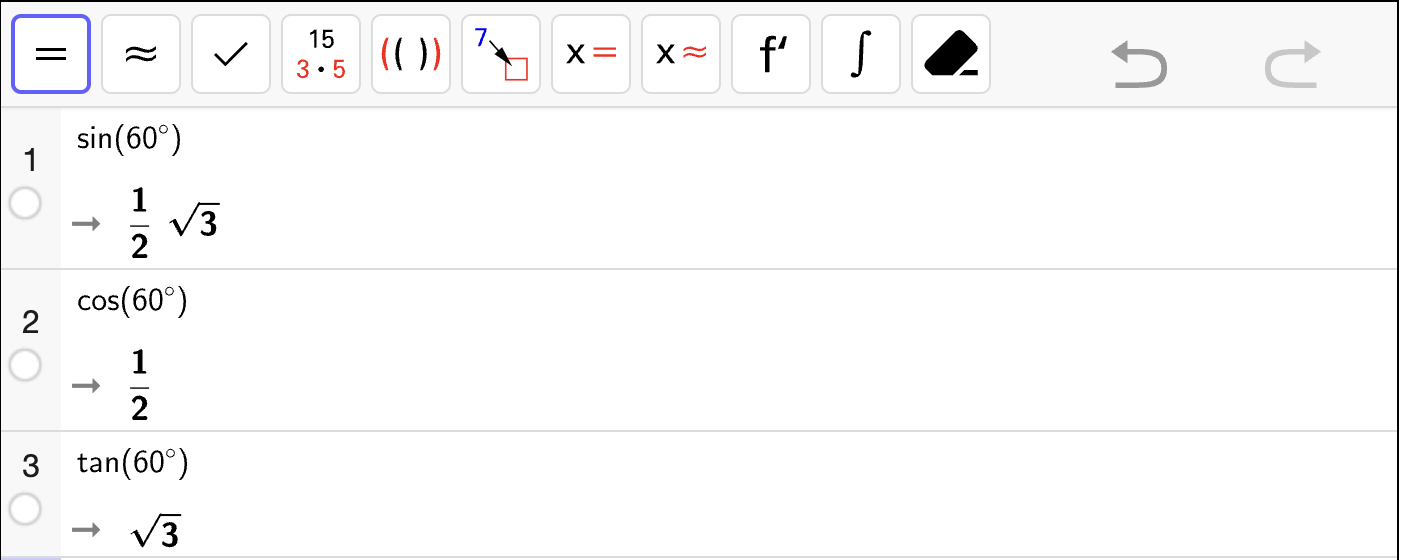
Vi ser at skjæringspunktet er \((-1, 3)\). Det er \(x\)-koordinaten som er løsningen av likningen, så løsningen er
Fasit
Løsning
Vi skriver inn uttrykkene på venstre og høyre side av likningen i algebrafeltet og trykker på (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktene. Se figuren nedenfor.
Vi ser at skjæringspunktet er \((-2, 3)\). Det er \(x\)-koordinaten som er løsningen av likningen, så løsningen er
Fasit
Løsning
Vi skriver inn uttrykkene på venstre og høyre side av likningen i algebrafeltet og trykker på (Skjæring mellom to objekt) etterfulgt av å trykke på hver graf for å finne skjæringspunktene. Se figuren nedenfor.

Vi ser at skjæringspunktet er \((4, 1)\). Det er \(x\)-koordinaten som er løsningen av likningen, så løsningen er
Oppgave 3
Løs likningene nedenfor algebraisk.
Fasit
Fasit
Fasit
Fasit
Oppgave 4
I programmet nedenfor løses en likning.
Bestem hvilken likning programmet løser.
Hvilke verdier er det programmet prøver ut for \(x\)?
Bestem verdien programmet skriver ut og sjekk svaret ditt ved å kjøre programmet.
Fasit
Programmet løser likningen \(x + 5 = 0\).
Programmet prøver ut verdiene \(x \in \set{-10, -9, \ldots, 9, 10}\).
Programmet skriver ut verdien \(-5\).
I programmet nedenfor løses en likning.
Bestem hvilken likning programmet løser.
Bestem verdien programmet skriver ut og sjekk svaret ditt ved å kjøre programmet.
I programmet nedenfor løses en likning.
Bestem hvilken likning programmet løser.
Bestem verdien programmet skriver ut og sjekk svaret ditt ved å kjøre programmet.
I programmet nedenfor løses en likning.
Bestem hvilken likning programmet løser.
Bestem verdien programmet skriver ut og sjekk svaret ditt ved å kjøre programmet.
Oppgave 5
Grafene til to lineære funksjoner \(f\) og \(g\) er vist i figuren nedenfor. Funksjonsuttrykkene er gitt ved
Løs likningene nedenfor ved hjelp av figuren der det er mulig. Hvis ikke må du bruke en annen metode.
Løs likningen
Fasit
Løs likningen
Fasit
Løs likningen
Fasit
Løs likningen
Fasit
Oppgave 6
En lineær funksjon \(f\) er gitt ved
Bestem i hvilket punkt grafen til \(f\) skjærer \(x\)-aksen.
Fasit
Bestem i hvilket punkt grafen til \(f\) skjærer linja \(y = 2\).
Fasit
En annen lineær funksjon \(g\) er gitt ved
Bestem i hvilket punkt grafen til \(f\) og \(g\) skjærer hverandre.
Fasit
Oppgave 7
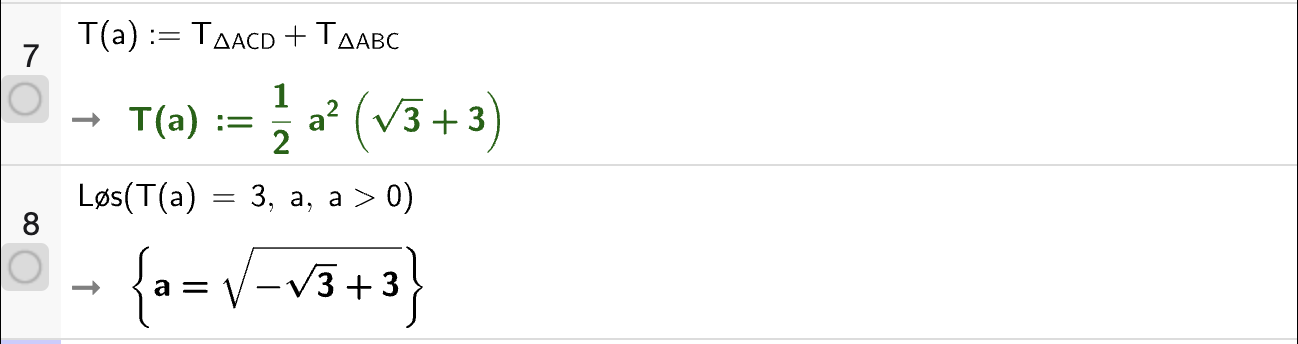
Bruk CAS til å løse likningene nedenfor.
Hvordan løser jeg en likning med CAS?
Nedenfor ser du en gif som viser hvordan man kan løse en likning med CAS. Du trenger bare å åpne CAS-vinduet og gjøre slik det vises i gif-en.

For å lage en brøk i CAS, skriver du bare telleren etterfulgt av skråstrek
/. Deretter kan du skrive nevneren.
Oppgave 8
Fyll ut programmet nedenfor slik at det løser likningen
Fyll ut programmet nedenfor slik at det løser likningen
Fyll ut programmet nedenfor slik at det løser likningen
Fyll ut programmet nedenfor slik at det løser likningen
Oppgave 9
To lineære funksjoner er gitt ved
Bruk CAS til å løse likningen
Bruk CAS til å løse likningen
Bruk CAS til å løse likningen
