12. Lineære ulikheter#
Læringsmål
Kunne løse lineære ulikheter grafisk, algebraisk ved regning og med CAS.
Vi skal se på tre strategier for å løse lineære ulikheter:
Grafisk løsning: Vi tegner grafen til ulikheten og ser hvilke verdier som oppfyller den.
Algebraisk løsning: Vi løser ulikheten ved å bruke algebraiske metoder, som å isolere variabelen. Dette kan vi gjøre ved regning eller med CAS.
Grafisk løsning#
For å løse en lineær ulikhet grafisk, tegner vi grafen til den tilhørende lineære funksjonen og ser hvilke verdier som oppfyller ulikheten. Dette innebærer først å lete etter skjæringspunkter, og deretter sjekke om grafen ligger over eller under en graf. La oss se på et eksempel:
Eksempel 1
Nedenfor vises grafen til funksjonen
Bruk grafen til å løse ulikheten
Løsning
Grafen til \(f\) skjærer \(x\)-aksen i \(x = 2\). Siden vi skal bestemme når \(f(x) \geq 0\), må vi sjekke hvor grafen til \(f\) ligger over eller på \(x\)-aksen. Vi ser fra grafen at når \(x > 2\) ligger grafen over \(x\)-aksen. Siden grafen til \(f\) er på \(x\)-aksen når \(x = 2\), så er løsningen av ulikheten
La oss se på et eksempel der vi har en annen type ulikhet:
Eksempel 2
Løs ulikheten
Løsning
Vi tegner først grafen til \(f(x) = 2x - 1\) og så undersøker vi hvor grafen til \(f\) ligger under linja \(y = 3\).
Vi ser at grafen til \(f\) skjærer linja \(y = 3\) når \(x = 2\). Vi ser også at grafen til \(f\) ligger under denne linja så lenge \(x < 2\). Dermed er løsningen av ulikheten
La oss se på et siste eksempel der vi har en ulikhet der både venstre og høyre side er lineære funksjoner:
Eksempel 3
Løs ulikheten
Løsning
Vi tegner grafene til
Løsningen av ulikheten vil være mengden av \(x\)-verdier der grafen til \(f\) ligger under eller på grafen til \(g\). Grafene skjærer hverandre når \(x = 3\). Før dette punktet, så ligger grafen til \(f\) under grafen til \(g\) som betyr at løsningen av ulikheten er
Algebraisk løsning#
Ved regning#
Å løse lineære ulikheter algebraisk likner en del på å løse lineære likninger. Den store forskjellen ligger i hvordan vi håndterer ulikhetstegnene. Når vi jobber med en lineær likning, trenger vi ikke tenke oss om når vi ganger med et negativt tall på hver side av likheten. Når det kommer til en lineær ulikhet, må vi imidlertid holde tunga rett i munnen å passe på at vi snur ulikhetstegnet når vi ganger eller deler med et negativt tall.
La oss se på et eksempel.
Eksempel 4
Løs ulikheten
Løsning
Vi starter med å trekke fra \(3x\) på hver side av ulikheten:
Dette gir oss
Deretter plusser på vi på \(1\) på hver side:
som gir oss
Så ganger vi med \((-1)\) på hver side av ulikheten, men da må vi passe på at vi snur ulikhetstegnet:
Dermed er løsningen av ulikheten
Med CAS#
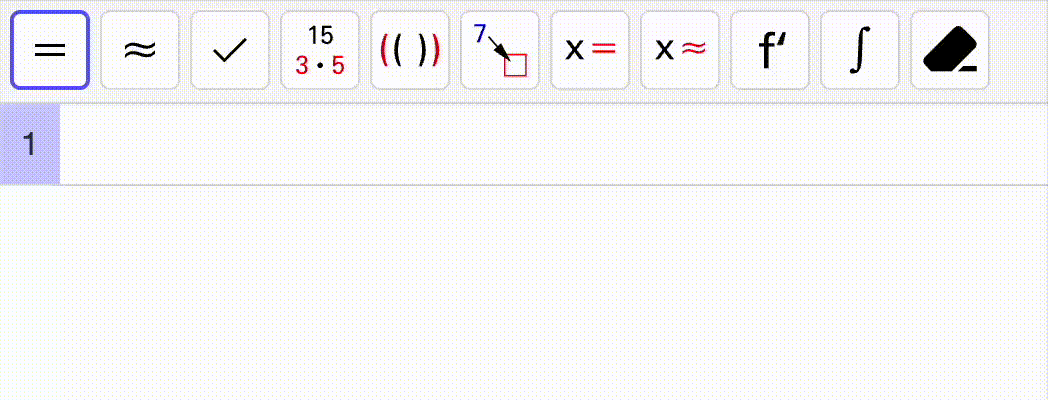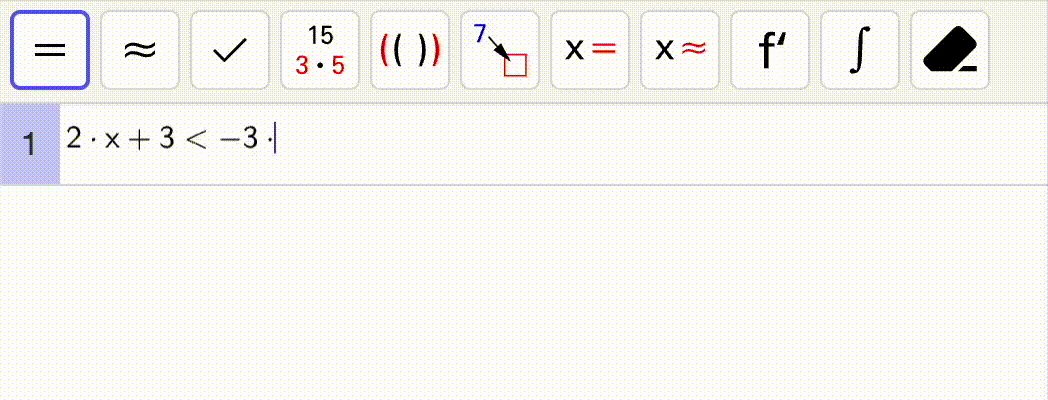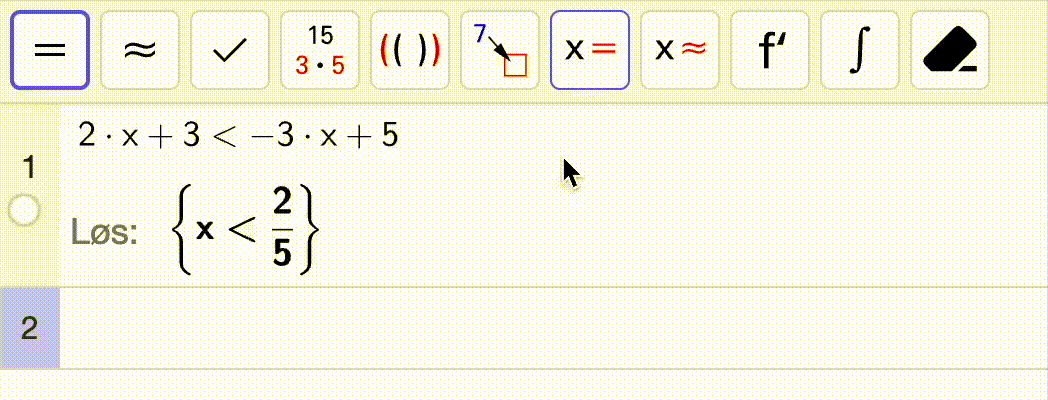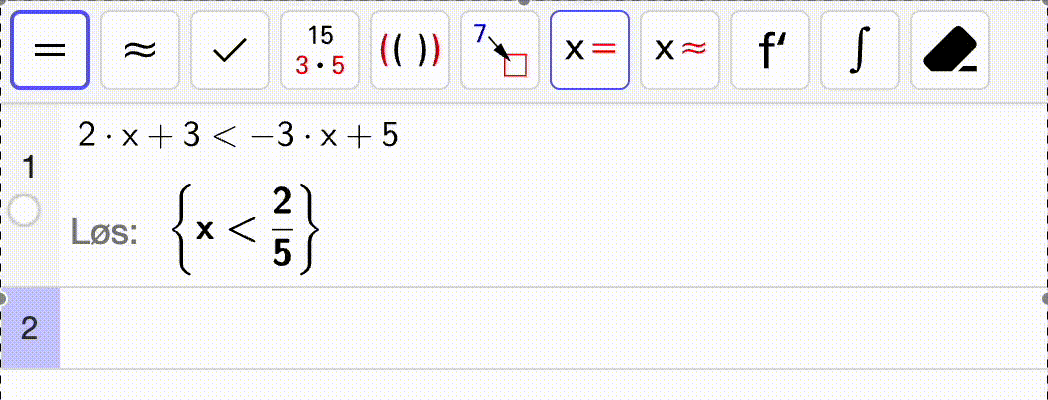
Vi kan få datamaskinen til å løse lineære ulikheter for oss og gi et svar på samme måte som vi ville fått dersom vi utførte regningen selv. La oss se på et eksempel:
Eksempel 5
Løs ulikheten
Løsning
Vi bruker CAS til å løse ulikheten slik som vi viser i gif-en nedenfor:
Fra gif-en ser vi at løsningen er