Oppgaver: Lineære likningssystemer#
Oppgave 1
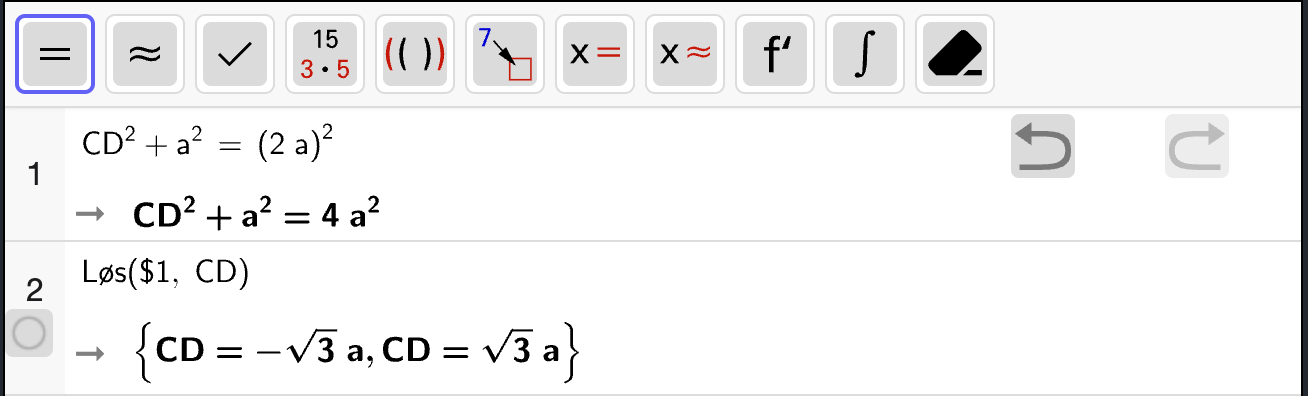
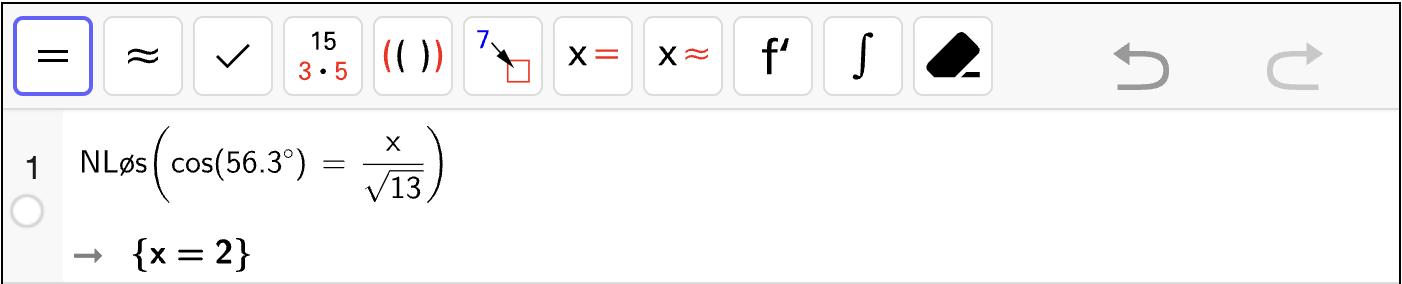
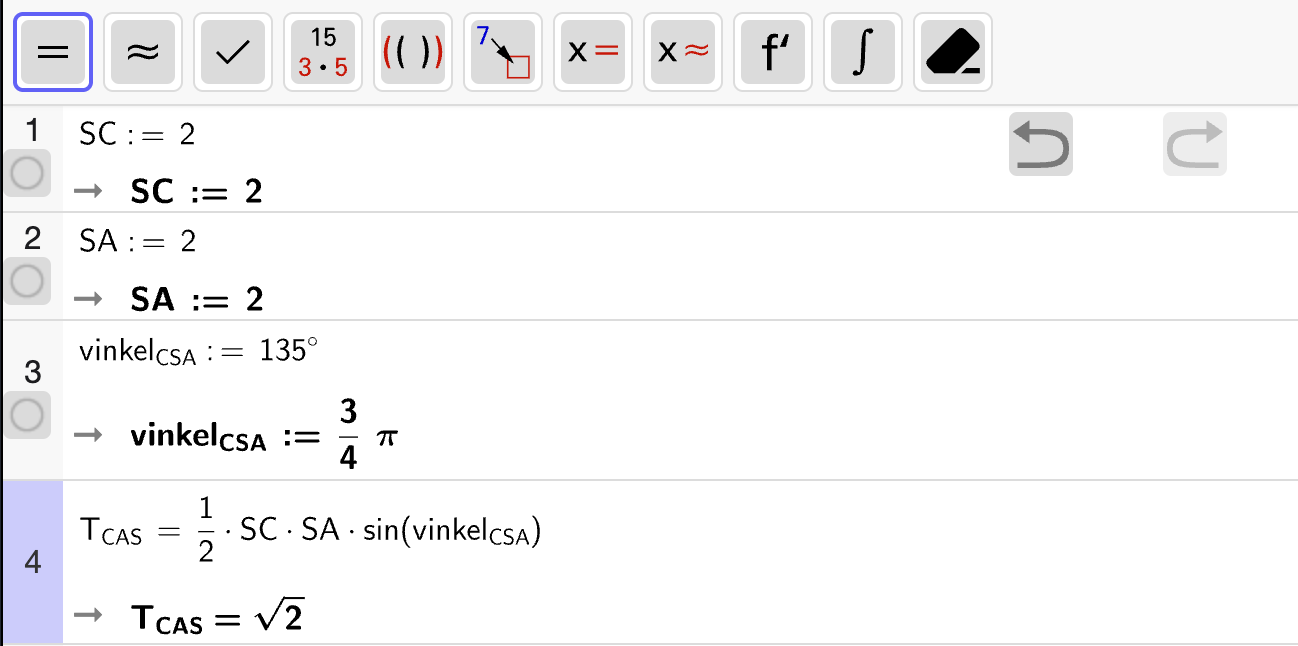
Bruk figurene til å løse likningssystemene.
Oppgave 2
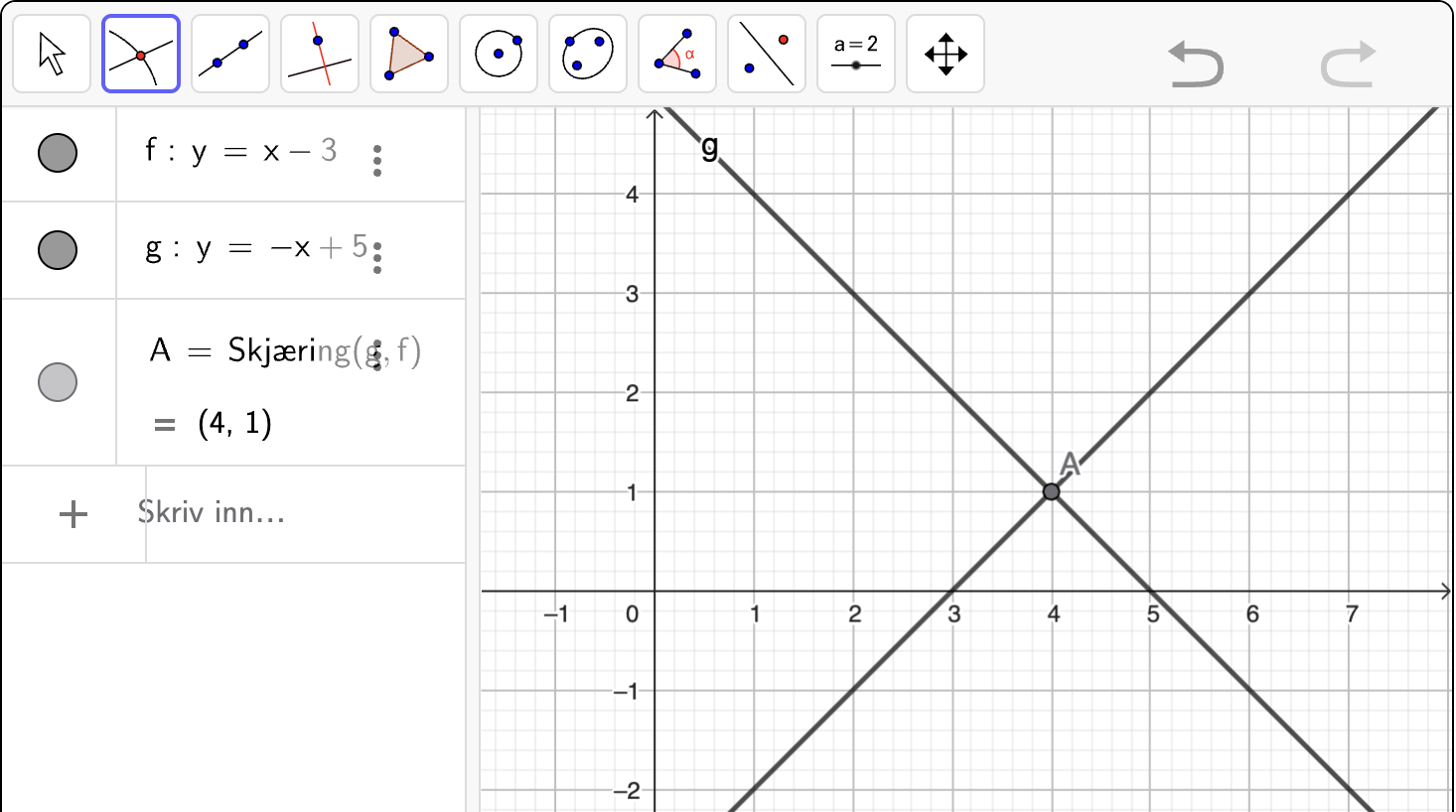
Hvordan løser jeg et likningssystem grafisk med Geogebra?
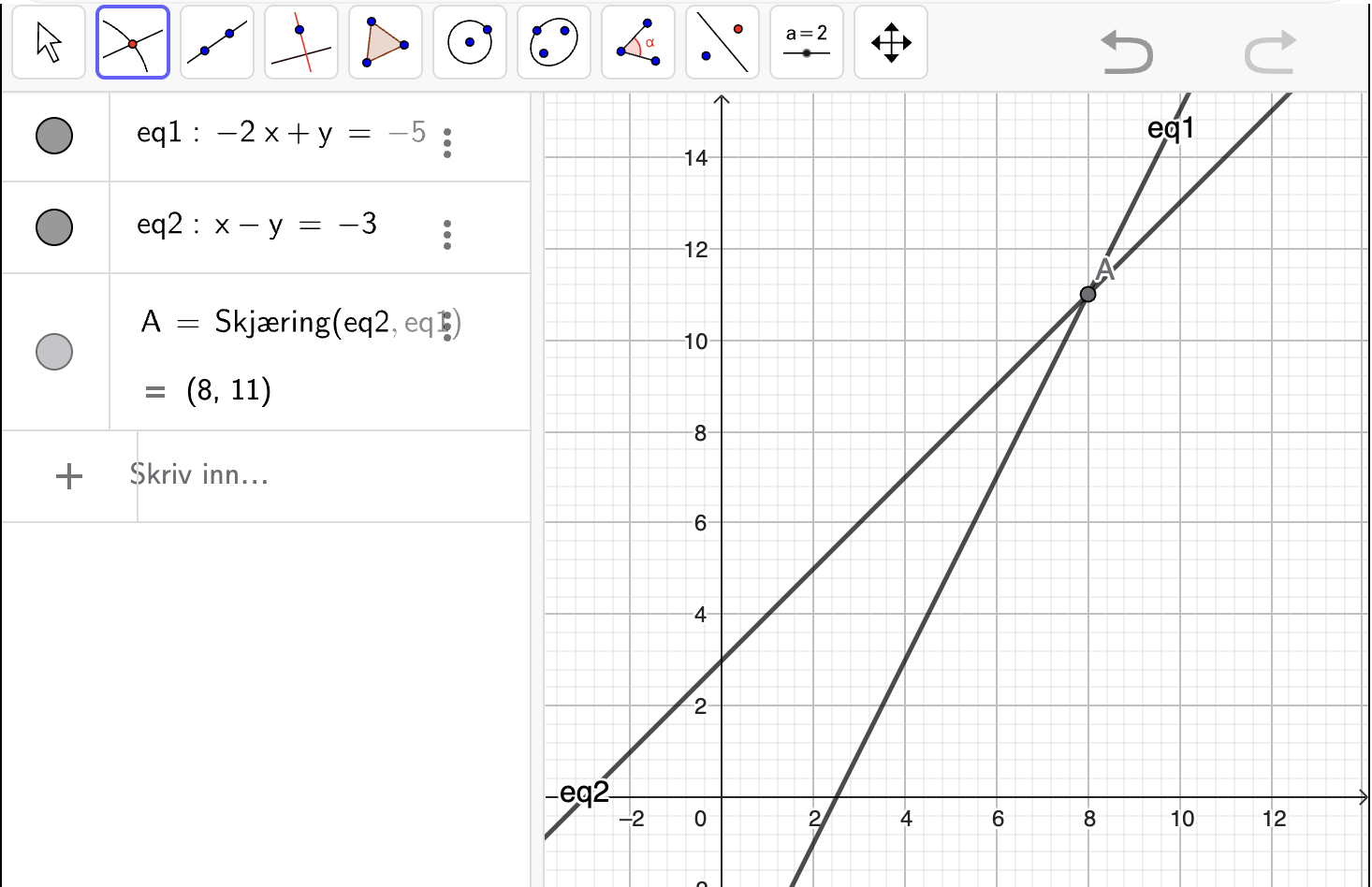
Nedenfor vises en gif som viser hvordan man løser et likningssystem med grafvinduet i Geogebra:
Løs likningsystemet nedenfor grafisk.
Fasit
Løs likningsystemet nedenfor grafisk.
Fasit
Løs likningsystemet nedenfor grafisk.
Fasit
Løs likningsystemet nedenfor grafisk.
Fasit
Oppgave 3
Bruk innsettingsmetoden til å løse likningssystemene.
Fasit
Løsning
Vi nummererer likningene:
Vi løser likning \(\t{I}\) med hensyn på \(y\):
Deretter setter vi dette uttrykket inn i likning \(\t{II}\):
Deretter bestemmer vi \(y\) ved å sette \(x = 3\) inn i likning \(\t{I}\):
Dermed er
Fasit
Løsning
Vi nummererer likningene først:
Først løser vi likning \(\t{II}\) med hensyn på \(x\):
Deretter setter vi dette uttrykket inn i likning \(\t{I}\):
Deretter setter vi \(y = 1\) inn i likning \(\t{II}\) for å bestemme \(x\):
Dermed er løsningen
Fasit
Løsning
Vi nummererer likningene først:
Vi løser likningen \(\t{II}\) med hensyn på \(x\):
Deretter setter vi dette uttrykket for \(x\) inn i likning \(\t{I}\):
Deretter setter vi \(y = \dfrac{1}{2}\) inn i likning \(\t{II}\) for å bestemme \(x\):
Dermed er
Fasit
Løsning
Vi nummererer likningene først:
Vi løser likning \(\t{II}\) med hensyn på \(x\):
Deretter setter vi dette uttrykket for \(x\) inn i likning \(\t{I}\):
Deretter setter vi \(y = -\dfrac{3}{2}\) inn i likning \(\t{II}\) for å bestemme \(x\):
Dermed er
Oppgave 4
Bruk addisjonsmetoden til å løse likningssystemene.
Fasit
Løsning
Vi nummerer likningene først:
Vi legger sammen likning \(\t{I}\) og likning \(\t{II}\):
Dermed får vi en likning som vi kan løse for \(x\):
Deretter setter vi denne verdien for \(x\) inn i likning \(\t{I}\) for å bestemme \(y\):
Dermed er løsningen
Fasit
Løsning
Vi nummererer likningene og legger de sammen:
Da får vi likningen
Deretter setter vi inn \(y = \dfrac{1}{2}\) i likning \(\t{I}\) for å bestemme \(x\):
Dermed er
Hint
Her må du gange én av likningene med et tall før du plusser eller trekker den fra den andre likningen for at en variabel skal forsvinne.
Fasit
Løsning
Vi nummererer likningene først:
Deretter ganger vi likning \(\t{I}\) med \(-2\):
Så legger vi sammen de to likningene:
Dermed får vi likningen
Deretter setter vi inn \(y = 1\) i likning \(\t{I}\) for å bestemme \(x\):
Dermed er
Fasit
Løsning
Først nummererer vi likningene:
Deretter gjør vi om på likningssystemet ved å gange likning \(\t{II}\) med \(2\):
Hvis vi nå tar den første likningen og trekker fra den andre, så får vi:
Da får vi
Deretter setter vi inn \(y = -\dfrac{7}{5}\) i likning \(\t{II}\) for å bestemme \(x\):
Dermed er
Oppgave 5
Én av figurene i hver oppgave hører til likningssystemet. Bestem riktig figur og bruk den til å løse likningssystemene.
Hint
Her må du kanskje skrive om likningene fra \(Ax + By = C\) til \(y = ax + b\) så du kan gjenkjenne hvilke grafer som hører til hvilke likninger.
Fasit
Løsning
Vi kan starte med å sjekke hva \(y\) er når \(x = 0\) i hver likning. Da får vi:
Dette stemmer bare med figur \(B\) siden de to linjene skjærer \(y\)-aksen i \((0, 1)\) og \((0, -1)\). Grafene skjærer hverandre i \((-2, 3)\) som betyr at løsningen av likningssystemet er
Fasit
Løsning
Vi kan sjekke hvor grafene skjærer \(x\)-aksen ved å sette inn \(y = 0\):
Altså skjærer grafene til likningene gjennom \(x\)-aksen når
Det passer bare med figur A. Grafene hverandre i \((2, 1)\), så løsningen av likningssystemet er
Oppgave 6
Bruk CAS til å løse likningssystemene.
Hvordan løser jeg et likningssystem med CAS?
Nedenfor ser du en gif som viser hvordan man løser et likningssystem med CAS:
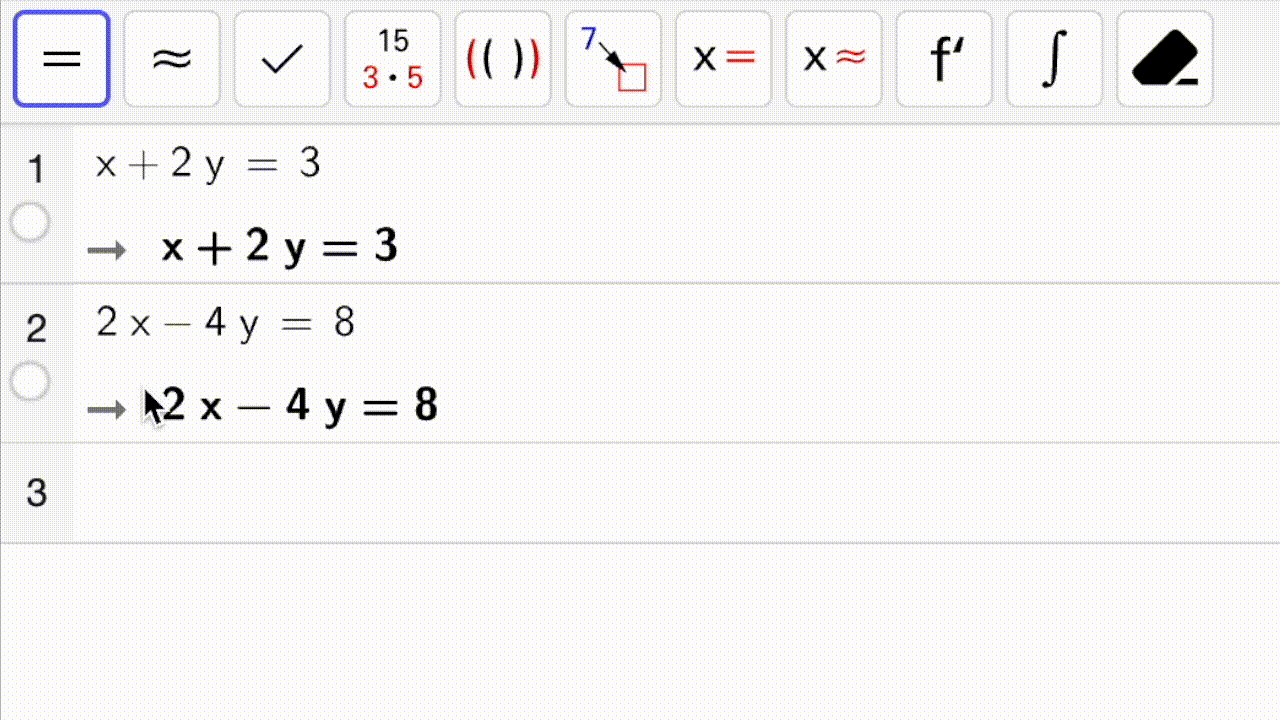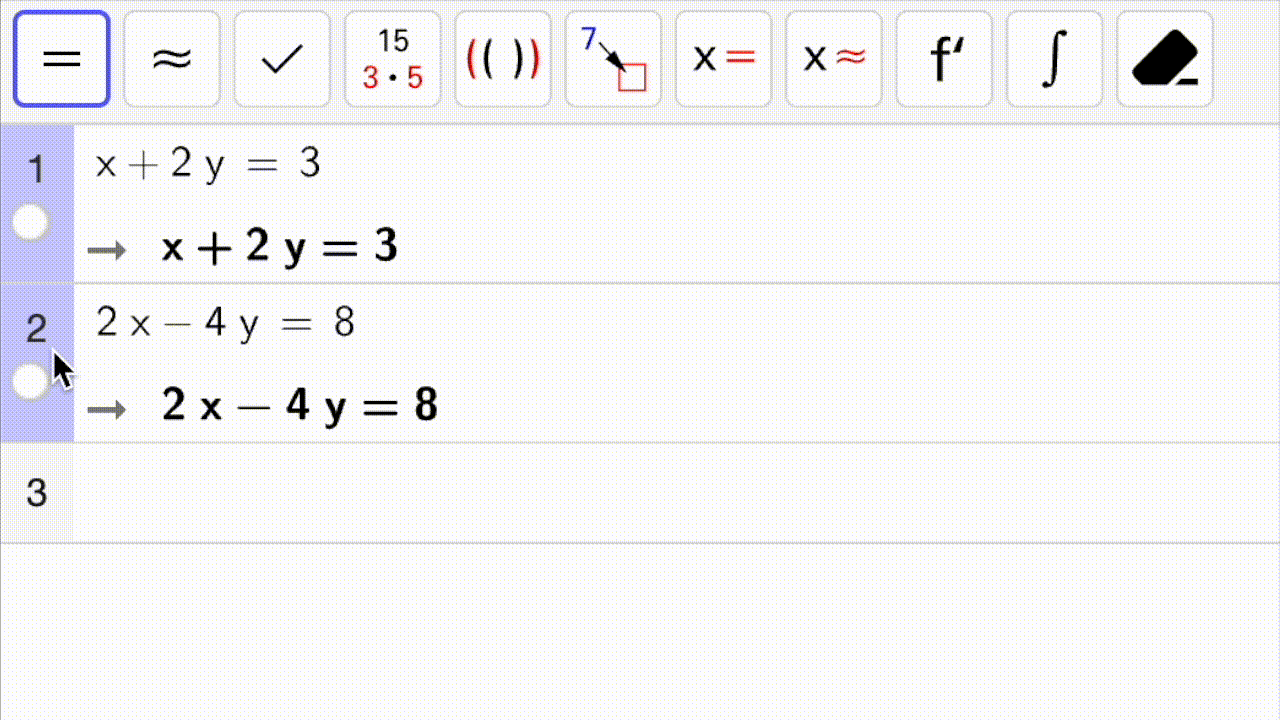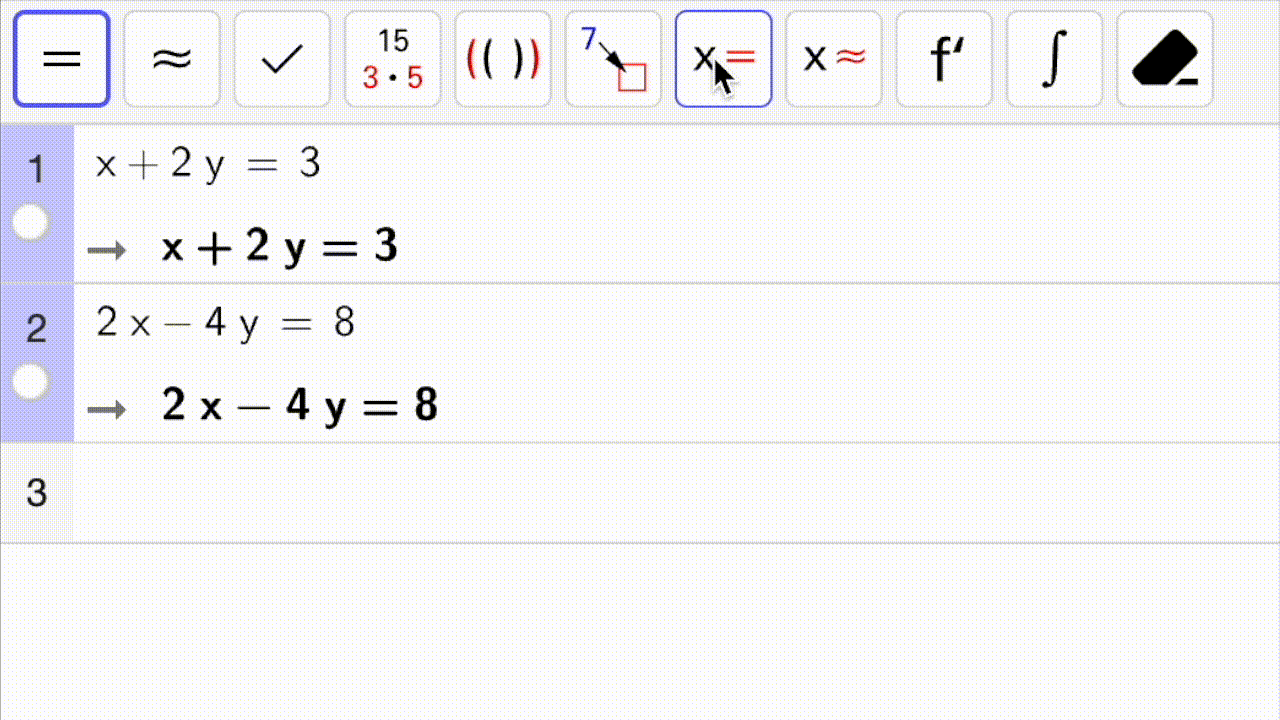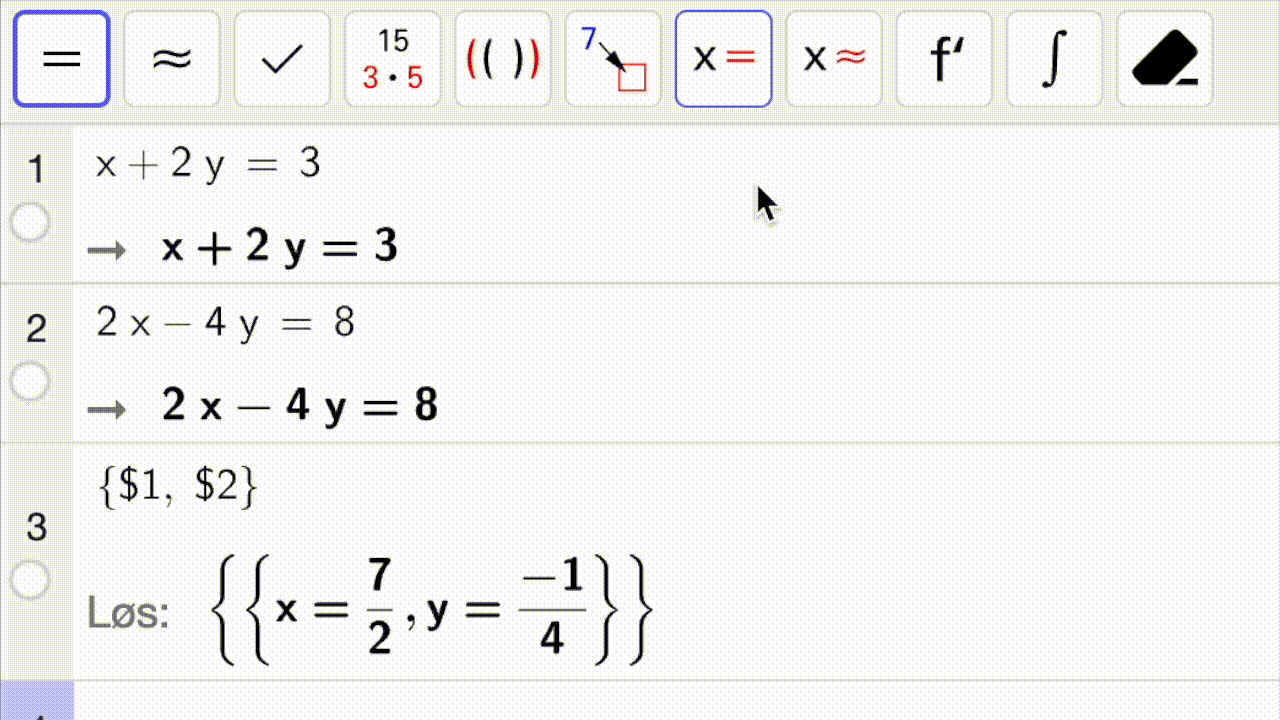
Fasit
Fasit
Fasit
Oppgave 7
Nedenfor vises noen programmer som løser et likningssystem. Tolk hvilket likningssystem hvert program løser og bruk CAS til å forutsi hva programmet skriver ut.
Oppgave 8
Fyll ut programmet nedenfor slik at de løser likningssystemene.
Løsning
1for x in range(-10, 11):
2 for y in range(-10, 11):
3 if x + y == 0 and -2*x + 4*y == 6:
4 print((x, y))
som gir utskriften
(-1, 1)
Løsningen er dermed
Løsning
1for x in range(-10, 11):
2 for y in range(-10, 11):
3 if x + 1/2 * y == 2 and 1/6 * x + 1/4 * y == 0:
4 print((x, y))
som gir utskriften
(3, -2)
Dermed er løsningen
Løsning
1for x in range(-10, 11):
2 for y in range(-10, 11):
3 if 2*x + y == -1 and 5*x + y == 5:
4 print((x, y))
som gir utskriften
(2, -5)
Dermed er løsningen
Løsning
1for x in range(-10, 11):
2 for y in range(-10, 11):
3 if 2*x - 5*y == 11 and -4*x + y == 5:
4 print((x, y))
som gir utskriften
(-2, -3)
Dermed er løsningen
Oppgave 9
Bruk CAS til å løse likningssystemene nedenfor.
Oppgave 10
I noen sammenhenger er det naturlig å bruker likningssystemer til å modellere praktiske situasjoner.
En bygård har 40 leiligheter med til sammen 90 rom.
Hvor mange leiligheter har 2 rom og hvor mange har 3 rom?
En butikk selger små og store sekker med hundemat. De små sekkene veier \(4.5\) kg og de store veier \(12\) kg.
En dag solgte butikken \(80\) sekker. Sekkene veide til sammen \(720\) kg.
Hvor mange små og hvor mange store sekker solgte butikken denne dagen?
En kino solgte 250 billetter til en forestilling. Barnebilletten koster 90 kr, og voksenbilletten koster 140 kr. Den totale billettinntekten var 27 000 kr.
Hvor mange barnebilletter og hvor mange voksenbilletter ble solgt?
Et skoletrinn skal på tur og bestiller busser. En stor buss har plass til 60 elever, og en liten buss har plass til 24 elever. De bestiller totalt 5 busser, og det er akkurat plass til hele trinnet på 228 elever.
Hvor mange store og hvor mange små busser ble bestilt?
Oppgave 11
Et likningssystem har løsningen
Lag et likningssystem som har denne løsningen.
Fasit
Et mulig likningssystem er:
\begin{align*} 2x + 3y &= 5 \ -x + 2y &= 8 \end{align*}}