Oppgaver: Lineære ulikheter

Oppgaver: Lineære ulikheter#

Oppgave 1

Figuren nedenfor viser grafen til \(f(x) = x + 3\).

Bruk figuren til å løse ulikheten

\[ x + 3 < 0. \]
../../../_images/a20.svg

Figuren nedenfor viser grafen til \(f(x) = -2x + 4\).

Bruk figuren til å løse ulikheten

\[ -2x + 4 \leq 0. \]
../../../_images/b19.svg

Figuren nedenfor viser grafen til \(f(x) = \dfrac{1}{2}x - 1\).

Bruk figuren til å løse ulikheten

\[ \frac{1}{2}x - 1 > 0. \]
../../../_images/c20.svg

Figuren nedenfor viser grafen til \(f(x) = 3x - 6\).

Bruk figuren til å løse ulikheten

\[ 3x - 6 \geq 0. \]
../../../_images/d19.svg

Oppgave 2

Bruk graftegner i Geogebra til å løse ulikhetene nedenfor.

\[ 2x + 6 \leq -x + 3 \]
\[ -2x + 3 > 1 \]
\[ \dfrac{3}{2}x + 1 < x + 2 \]
\[ 2x + 5 \geq -3x + 2 \]

Oppgave 3

Løs ulikhetene algebraisk.

\[ 2x + 5 < -2 \]
\[ 3x + 2 > -2x + 7 \]
\[ \dfrac{1}{5}x + 3 \leq -2x + 3 \]
\[ -2x + \dfrac{1}{2} \geq 5x + 3 \]

Oppgave 4

Hvordan løser jeg en ulikhet med CAS?

Nedenfor ser du en gif som løser ulikheten

\[ 2x + 3 < -3x + 5 \]
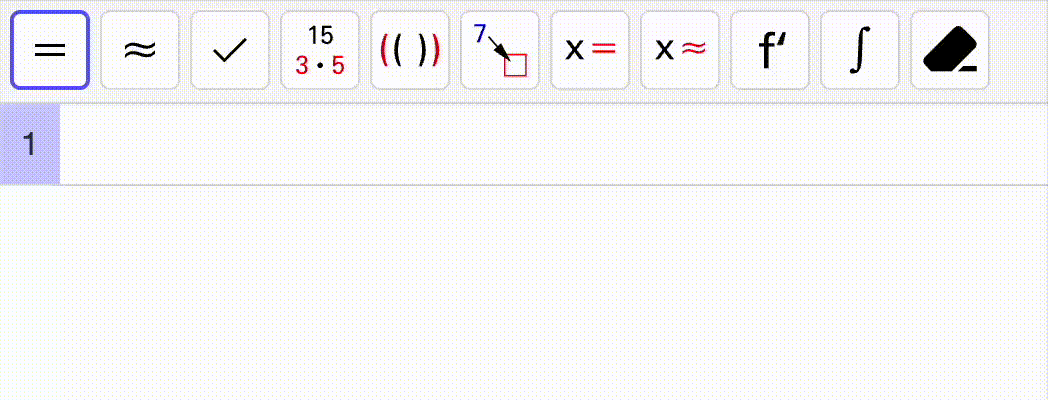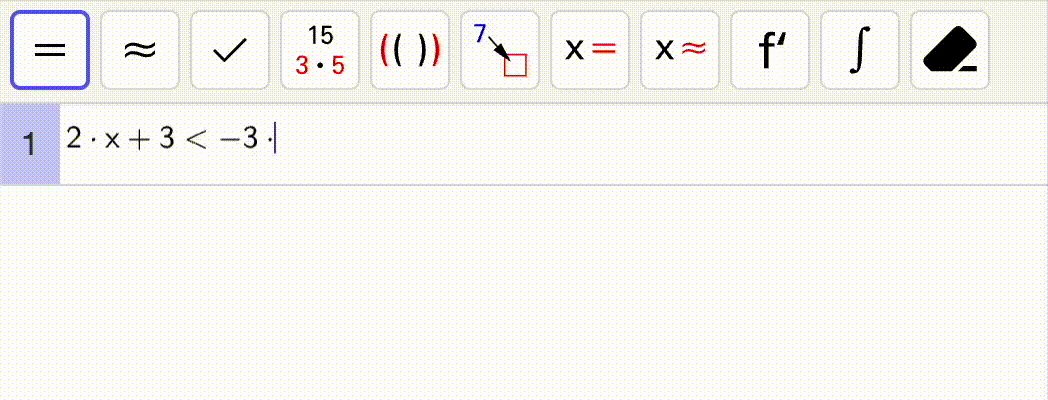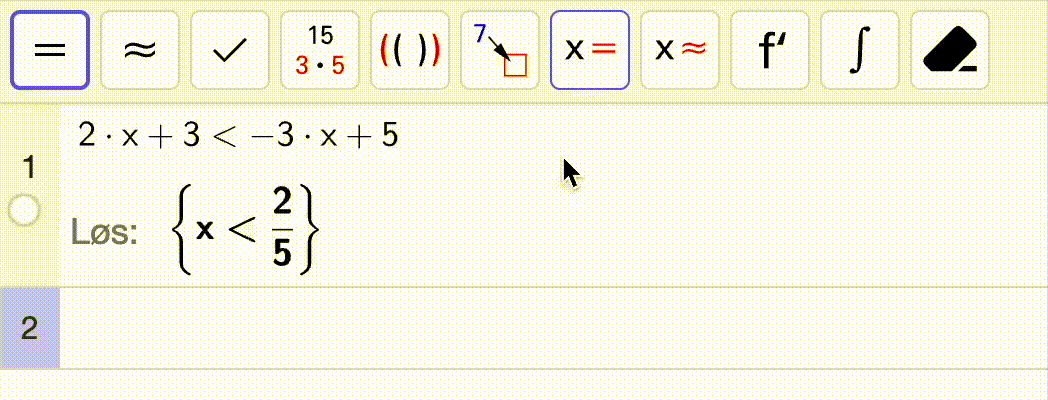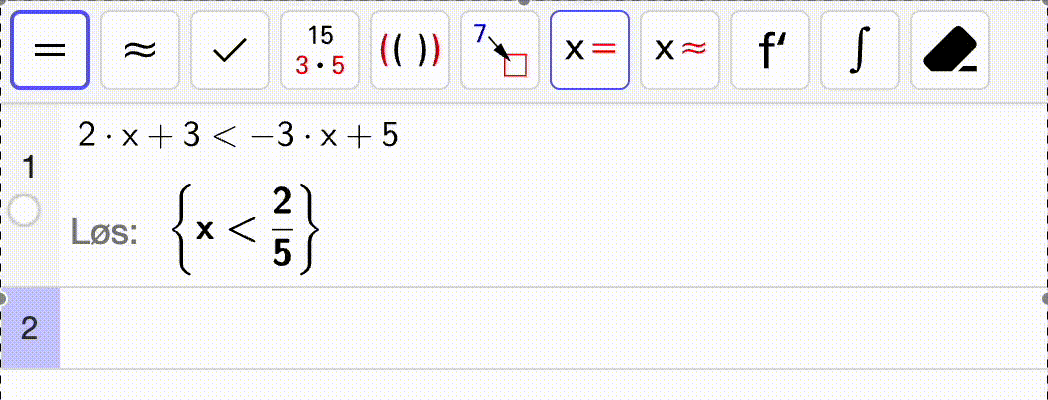
../../../_images/cas1.gif

Fra utskriften ser vi at løsningen er

\[ x < \dfrac{2}{5} \]

Bruk CAS til å løse ulikhetene.

\[ -2x + 3 > 2x + 6 \]
\[ 3x - 2 \geq \dfrac{1}{3}x + 1 \]
\[ -2x + 9 \leq 3x + 5 \]
\[ -7x + 3 < 3x + 7 \]

Oppgave 5

I figuren nedenfor vises grafene til to lineære funksjoner \(f\) og \(g\).

../../../_images/figur104.svg

Løs ulikheten

\[ f(x) < 0 \]

Løs ulikheten

\[ g(x) \geq 3 \]

Løs ulikheten

\[ f(x) \leq g(x) \]

Oppgave 6

To lineære funksjoner \(f\) og \(g\) er gitt ved

\[ f(x) = -\dfrac{1}{2}x + 3 \qog g(x) = 2(x - 1) + 3 \]

Løs ulikheten

\[ f(x) > 0 \]

Løs ulikheten

\[ g(x) < -2 \]

Løs ulikheten

\[ f(x) \geq g(x) \]