Eksamen vår 2025

Del 1

Oppgavene i del 1 skal løses uten hjelpemidler.

Oppgave 1 (2 poeng)

En funksjon \(f\) er gitt ved

\[ f(x) = \dfrac{12x - 3}{2x + 1} \]

Bestem likningene for eventuelle asymptoter til grafen til \(f\).

Fasit

• Horisontal asymptote: \(y = 6\)

• Vertikal asymptote: \(x = -\dfrac{1}{2}\)

Løsning

Den horisontale asymptoten kan vi bestemme ved å utføre polynomdivisjon og lese av likningen til kvotienten:

som viser at kvotienten er \(y = 6\). Dermed er likningen til den horisontale asymptoten \(y = 6\).

For å bestemme en eventuell vertikal asymptote, ser vi etter nullpunkter til nevneren som ikke er felles med nullpunktene til telleren. Da har vi at

\[ 2x + 1 = 0 \liff x = -\dfrac{1}{2}. \]

Samtidig må vi sjekke at nevneren ikke har dette som nullpunkt, som vi kan se ved at

\[ 12x - 3 = 0 \liff x = \dfrac{1}{4}. \]

Dermed er vi sikre på at \(x = -\dfrac{1}{2}\) svarer til en vertikal asymptote for grafen til \(f\).

---

Oppgave 2 (2 poeng)

Løs ulikheten

\[ x^2 - 4x - 12 \lt 0 \]

Fasit

\[ x \in \langle -2, 6 \rangle. \]

Løsning

Vi starter med å nullpunktsfaktorisere andregradspolynomet \(x^2 - 4x - 12\). Dette kan vi oppnå ved å bestemme røttene til polynomet ved hjelp av \(abc\)-formelen:

\[\begin{align*} x &= \dfrac{-(-4) \pm \sqrt{4^2 - 4\cdot 1 \cdot (-12)}}{2\cdot 1} \\ \\ &= \dfrac{4 \pm \sqrt{16 + 48}}{2} \\ \\ &= \dfrac{4 \pm \sqrt{64}}{2} \\ \\ &= \dfrac{4 \pm 8}{2} \\ \\ &= 2 \pm 4 \end{align*}\]

som gir

\[ x = 6 \or x = -2. \]

Dermed kan vi skrive

\[ x^2 - 4x - 12 = (x - 6)(x + 2). \]

Så tegner vi et fortegnsskjema for polynomet slik at vi kan lese av når uttrykket er negativt:

Fra fortegnslinja til polynomet, kan vi lese av at uttrykket er negativt når

\[ x \in \langle -2, 6 \rangle. \]

---

Oppgave 3 (1 poeng)

En andregradsfunksjon \(f\) har ett nullpunkt. Grafen til \(f\) skjærer \(y\)-aksen i punktet \((0, 9)\).

Bestem et mulig funksjonsuttrykk \(f(x)\) for andregradsfunksjonen \(f\).

Fasit

Mange mulige svar. Én mulighet er

\[ f(x) = (x - 3)^2 = x^2 - 6x + 9. \]

Løsning

Siden andregradsfunksjonen har ett nullpunkt, så må funksjonsuttrykket være på formen

\[ f(x) = a(x - r)^2 \]

for et eller annet nullpunkt \(x = r\) og en passende ledende koeffisient \(a\). Vi må sørge for at \(f(0) = 9\), som vi kan oppnå ved å sette \(r = 3\) og \(a = 1\) som gir

\[ f(x) = (x - 3)^2 = x^2 - 6x + 9. \]

Her kan vi lese av at konstantleddet er \(c = 9\), som betyr at grafen til \(f\) skjærer \(y\)-aksen i punktet \((0, 9)\).

Et annet alternativ kan være \(f(x) = (x + 3)^2 = x^2 + 6x + 9\), som også gir \(f(0) = 9\) og har ett nullpunkt i \(x = -3\).

---

Oppgave 4 (4 poeng)

a

Løs likningen

\[ x^3 - 7x^2 - 10x + 16 = 0 \]

Fasit

\[ x = -2 \or x = 1 \or x = 8. \]

Løsning

Vi starter med å lete etter heltallige røtter for tredjegradspolynomet med å se på mulige \(x\)-verdier som deler konstantleddet \(16\). De mulige kandidatene er da

\[ x \in \{\pm 1, \pm 2, \pm 4, \pm 8, \pm 16\} \]

Vi starter med \(x = 1\) og bruker et Horner-skjema:

der vi kan se at resten er \(0\) som betyr at

\[ x^3 - 7x^2 - 10x + 16 = (x - 1)(x^2 - 6x - 16). \]

Deretter bruker vi \(abc\)-formelen på andregradspolynomet for å bestemme de resterende røttene:

\[\begin{align*} x &= \dfrac{-(-6) \pm \sqrt{(-6)^2 - 4\cdot 1 \cdot (-16)}}{2\cdot 1} \\ \\ &= \dfrac{6 \pm \sqrt{36 + 64}}{2} \\ \\ &= \dfrac{6 \pm \sqrt{100}}{2} \\ \\ &= \dfrac{6 \pm 10}{2} \\ \\ &= 3 \pm 5 \end{align*}\]

som gir

\[ x = 8 \or x = -2. \]

Dermed er løsningen av likningen

\[ x = -2 \or x = 1 \or x = 8. \]

b

Funksjonen \(f\) er gitt ved

\[ f(x) = x^3 - 7x^2 - 10x + 16. \]

Hvilken av grafene nedenfor kan være grafen til \(f\)?
Husk å begrunne svaret ditt.

Fasit

Graf C.

Løsning

Fra oppgave a kan vi merke oss at

\[ f(x) = x^3 - 7x^2 - 10x + 16 = (x - 1)(x + 2)(x - 8) \]

Vi kan dermed se at \(f\) har to nullpunkter der \(x > 0\) og ett nullpunkt der \(x < 0\). Da kan vi eliminere graf A og graf D.

Vi kan også merke oss at den ledende koeffisientene til \(f(x)\) er positiv, som betyr at \(f(x) < 0\) når \(x\) er veldig negativ og \(f(x) > 0\) når \(x\) er stor og positiv. Graf B kan derfor elimineres siden denne grafen gjør det motsatte.

Dermed må grafen til \(f\) være graf C.

---

Oppgave 5 (6 poeng)

a

Bruk den likesidede trekanten ovenfor til å vise at \(\sin 30\degree = \cos 60\degree = \dfrac{1}{2}\)

Løsning

Trekanten som er likesidet er delt nøyaktig i to slik at vi får en \(30\degree\)-\(60\degree\)-\(90\degree\) trekant. Sett fra vinkelen som \(30\degree\) er den motstående kateten \(1\) og hypotenusen er \(2\). Dermed kan vi ved definisjonen av sinus skrive ned:

\[ \sin 30\degree = \dfrac{\text{motstående katet}}{\text{hypotenus}} = \dfrac{1}{2}. \]

Tilsvarende kan vi ut ifra vinkelen som er \(60\degree\) merke oss at den hosliggende kateten er \(1\) og hypotenusen er \(2\). Dermed kan vi skrive ned:

\[ \cos 60\degree = \dfrac{\text{hosliggende katet}}{\text{hypotenus}} = \dfrac{1}{2}. \]

b

Gitt en trekant \(ABC\) der \(AB = 10\), \(AC = 6\) og \(\angle A = 30\degree\).

Bestem arealet av trekanten.

Fasit

\[ T_{\triangle ABC} = 15. \]

Løsning

Vi bruker arealsetningen ut ifra vinkel \(\angle A\) siden denne vinkelen er spent ut av sidelengdene \(AB\) og \(AC\). Da blir arealet av trekanten

\[ T_{\triangle ABC} = \dfrac{1}{2} \cdot AB \cdot AC \cdot \sin A = \dfrac{1}{2} \cdot 10 \cdot 8 \cdot \sin 30\degree = \dfrac{1}{2} \cdot 10 \cdot 6 \cdot \dfrac{1}{2} = 15. \]

c

Gitt en trekant \(PQR\) der \(PQ = 8\), \(PR = 3\) og \(\angle P = 60\degree\).

Bestem lengden av siden \(QR\).

Fasit

\[ QR = 7. \]

Løsning

Vi bruker cosinussetningen ut ifra vinkel \(\angle P\) siden denne siden er spent ut av sidelengdene \(PQ\) og \(PR\), og \(x = QR\) er den motstående siden til \(P\) som gir

\[\begin{align*} x^2 &= 8^2 + 3^2 - 2 \cdot 8 \cdot 3 \cdot \cos 60\degree \\ \\ x^2 &= 64 + 9 - 2 \cdot 8 \cdot 3 \cdot \dfrac{1}{2} \\ \\ x^2 &= 64 + 9 - 24 \\ \\ x^2 &= 49 \\ \end{align*}\]

som gir \(x = \sqrt{49} = 7\). Dermed er lengden av siden \(QR\) gitt ved

\[ QR = 7. \]

---

Oppgave 6 (1 poeng)

Kari arbeider med algebraiske uttrykk, likninger og identiteter.
Hun prøver å løse likningen

\[ x^2 - 4 = (x + 2)(x - 2) \]

i et CAS-verktøy og får resultatet \(x = x\). Se nedenfor.

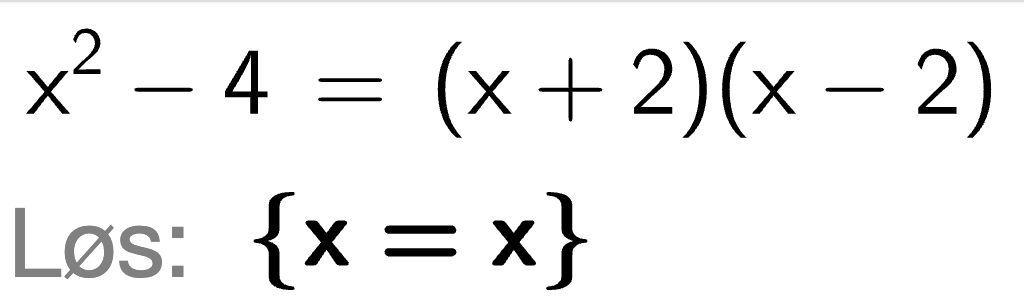
Ta utgangspunkt i dette resultatet og forklar Kari hva en identitet er.

Løsning

En identitet er en likning som er oppfylt for alle verdier av variabelen som inngår i likningen. Utskriften Kari får fra CAS-verktøyet sier at \(x = x\) som forteller oss at likningen er oppfylt uansett hvilken verdi \(x\) har. Dermed er likningen en identitet.

Vi kan legge merke til at likningen bare er et tilfelle av konjugatsetningen, som forklarer hvorfor likningen er oppfylt for alle verdier av \(x\).

---

Oppgave 7 (2 poeng)

Siri har laget programmet nedenfor.

def f(x):
    return x ** 2 + 2 * x - 15

x = -5
verdi = f(x)

while x <= 5:

    if f(x) < verdi:
        verdi = f(x)

    x = x + 1

print(verdi)

Hva finner Siri ut når hun kjører programmet?
Hvilken verdi skrives ut?

Fasit

Siri finner den minste verdien til \(f(x)\) og programmet skriver ut verdien \(-16\).

Løsning

Programmet starter med å sette verdi til \(f(-5)\). Deretter så øker programmet verdien til x med 1 frem til verdien er større enn \(5\). I hver iterasjon sjekker programmet om \(f(x)\) er mindre enn verdi. Hvis det er tilfelle, så oppdaterer programmet verdi til \(f(x)\). Det betyr at vi stadig ser etter en mindre verdi av \(f(x)\). Til slutt skriver programmet ut den minste verdien programmet fant. Dette vil svare til \(y\)-koordinaten til bunnpunktet på grafen til \(f\).

Vi kan bestemme denne verdien ved å første løse \(f'(x) = 0\) og deretter regne ut funksjonsverdien i punktet. Vi har

\[ f(x) = x^2 + 2x - 15 \limplies f'(x) = 2x + 2. \]

Så løser vi \(f'(x) = 0\):

\[ f'(x) = 0 \liff 2x + 2 = 0 \liff x = -1. \]

Dermed vil programmet skrive ut verdien

\[ f(-1) = (-1)^2 + 2\cdot (-1) - 15 = 1 - 2 - 15 = -16. \]

Siri finner dermed ut at den minste verdien til \(f(x)\) og programmet skriver ut verdien \(-16\).

---

Del 2

Oppgavene i del 2 kan løses med hjelpemidler.

Oppgave 1 (5 poeng)

Tabellen nedenfor viser antallet registrerte tilfeller av kikhoste i Norge noen måneder i perioden januar 2023 - oktober 2024.

Måned	Januar 2023	Mai 2023	Oktober 2023	Februar 2024	August 2024	Oktober 2024
Antall registrerte tilfeller	29	93	164	284	1035	1657

La \(x\) være antall måneder etter desember 2022, det vil si at \(x = 1\) tilsvarer januar 2023, \(x = 3\) tilsvarer mars 2023, og så videre.

a

Bruk opplysningene ovenfor til å vise at funksjonen \(K\) gitt ved

\[ K(x) = 27.8 \cdot 1.2^x \]

er en god modell for antall registrerte tilfeller av kikhoste i Norge i perioden januar 2023 - oktober 2024.

Løsning

Vi legger inn verdiene for \(x\) og \(K(x)\) i et regneark:

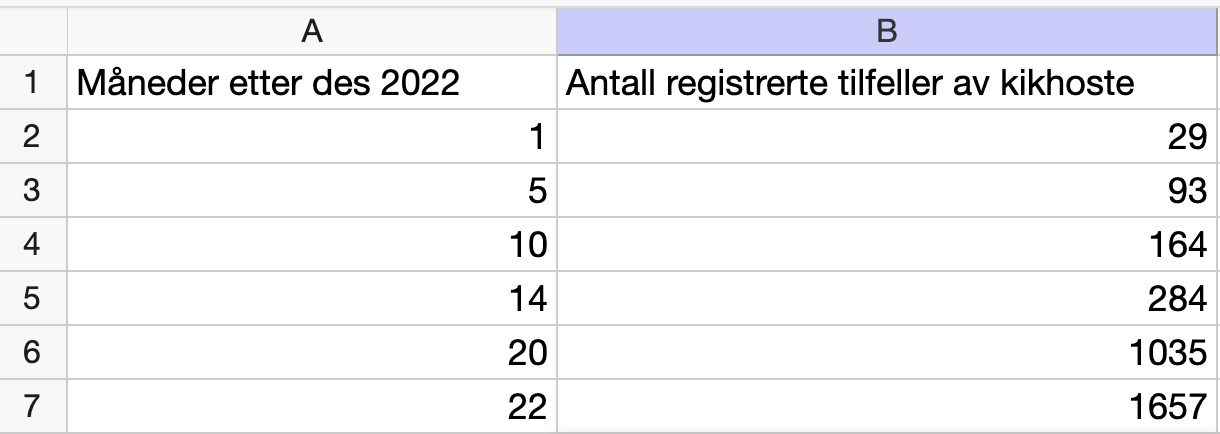
deretter utfører vi regresjon med en eksponentiell modell:

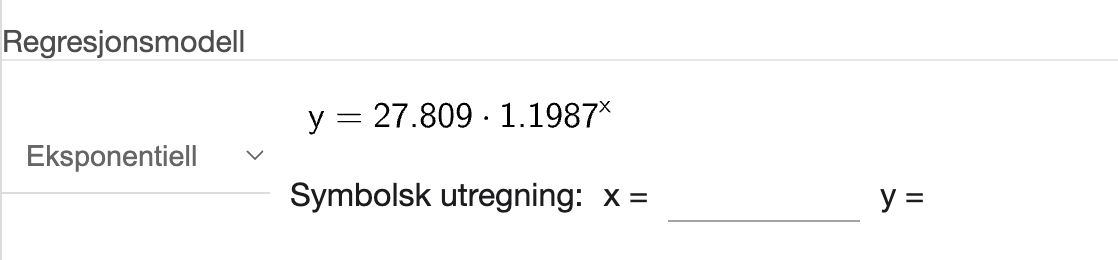
Fra skjermbilde ovenfor, kan vi se at modellen vi får er:

\[ K(x) = 27.809 \cdot 1.1987^x \approx 27.8 \cdot 1.2^x. \]

Dermed har vi vist at det oppgitte uttrykket for \(K(x)\) er en god modell for antall registrerte tilfeller av kikhoste i Norge i perioden januar 2023 - oktober 2024 der \(x\) er antall måneder etter desember 2022.

b

Bestem stigningstallet til den rette linjen som gjennom punktene \((4, K(4))\) og \((21, K(21))\).
Gi en praktisk tolkning av svaret du får.

Løsning

Vi bruker uttrykket for \(K(x)\) som er oppgitt i oppgaven. Stigningstallet til linja som går gjennom punktene \((4, K(4))\) og \((21, K(21))\) svarer til den gjennomsnittlige vekstfarten til \(K(x)\) i intervallet \([4, 21]\) som vi kan bestemme slik:

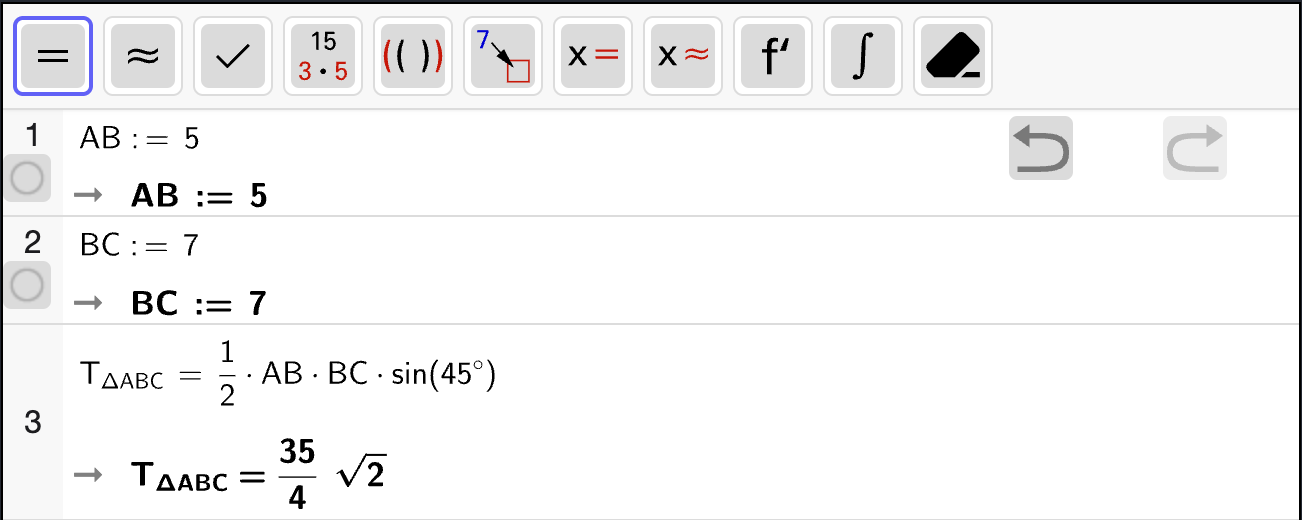
I celle 2 ser vi at stigningstallet er omtrent \(71.84\). Den praktiske tolkningen av dette er at antallet registrerte tilfeller av kikhoste økte i gjennomsnitt med ca. \(72\) tilfeller per måned i perioden fra april 2023 til september 2024 siden \(x = 4\) tilsvarer april 2023 og \(x = 21\) tilsvarer september 2024.

c

Hvor mange tilfeller av kikhoste vil bli registrert i Norge i mai 2025 ifølge modellen?

Løsning

Vi kan tolke problemet som at vi skal bestemme \(K(x)\) i mai 2025, som vi kan gjøre ved å sette

\[ x = 5 + 12\cdot 2 = 29 \]

Vi regner ut med CAS:

Dermed vil modellen gi at antall registrerte tilfeller av kikhoste i Norge i mai 2025 er omtrent \(K(29) \approx 4599\).

---

Oppgave 2 (2 poeng)

En butikk selger små og store sekker med hundemat. De små sekkene veier 4.5 kg og de store veier 12 kg.

En dag solgte butikken 80 sekker. Sekkene veide til sammen 720 kg.

Hvor mange små og store sekker solgte butikken den dagen?

Løsning

Vi lar \(x\) være antall små sekker og \(y\) være antall store sekker. Siden butikken solgte 80 sekker, får vi likningen:

\[ x + y = 80. \]

Siden sekkene til sammen veide 720 kg, får vi den andre likningen:

\[ 4.5x + 12y = 720 \]

Vi løser likningesystemet med CAS:

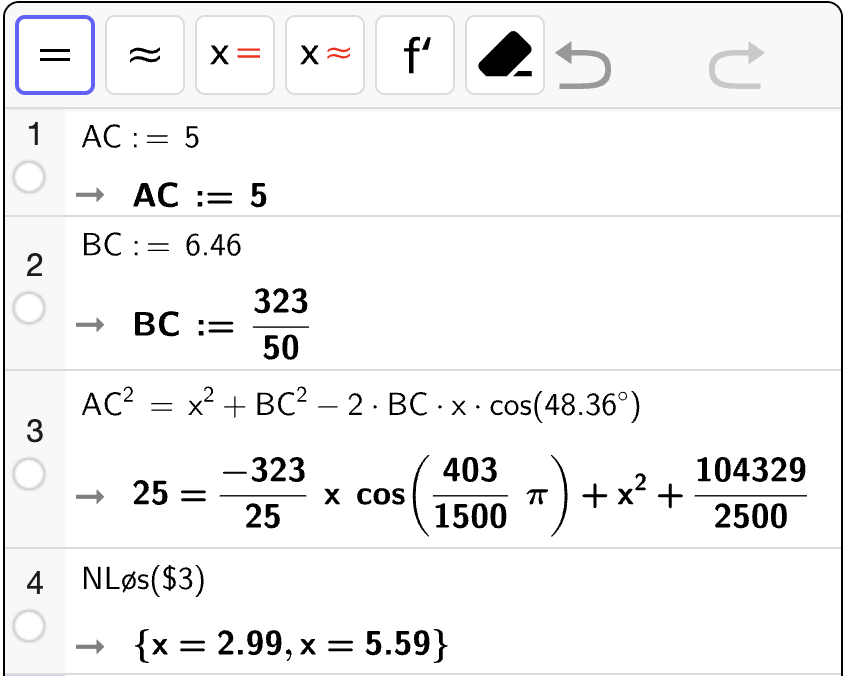
Fra utskriften kan vi lese av at

\[ x = 32 \or y = 48, \]

som betyr at butikken solgte 32 små sekker og 48 store sekker den dagen.

---

Oppgave 3 (4 poeng)

En tolvkant er innskrevet i en sirkel. Se figuren ovenfor. Tolvkanten er satt sammen av tolv like store likebeinte trekanter. Arealet av tolvkanten er \(120\).

a

Bestem diameter i sirkelen.
Gi svaret eksakt.

Fasit

\[ d = 4\sqrt{10}. \]

Løsning

Først kan vi merke oss at arealet til én trekant i tolvkanten er

\[ T = \dfrac{120}{12} = 10. \]

Deretter lar vi radius i sirkelen være \(r\) som betyr at arealet \(T\) av én trekant kan regnes ut med arealsetningen som:

\[ T = \dfrac{1}{2} \cdot r \cdot r \cdot \sin 30\degree \]

Da kan vi bestemme \(r\) ved å kreve at at \(T = 10\). Vi bestemmer \(r\) med CAS::

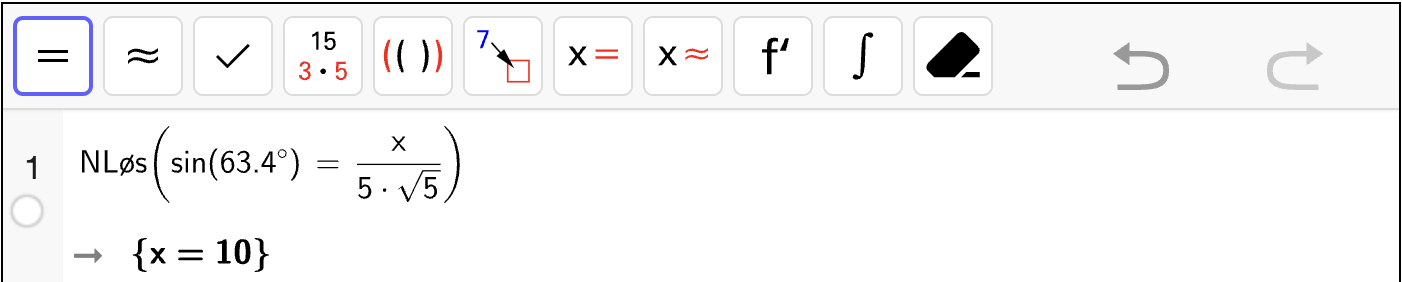
Som betyr at radius i sirkelen er \(r = 2\sqrt{10}\). Dermed er diameteren i sirkelen gitt ved

\[ d = 2r = 4\sqrt{10}. \]

b

Bestem omkretsen av tolvkanten.
Gi svaret eksakt.

Fasit

\[ \mathcal{O} = 24\left(\sqrt{15} - \sqrt{5}\right) \]

Løsning

For å bestemme omkretsen av tolvkanten, bruker vi cosinussetningen på én trekant i tolvkanten. Vi har at sidelengdene som spenner ut sentralvinkelen på \(30\degree\) er \(r = 2\sqrt{10}\). Vi lar den motstående siden være \(x\). Da kan vi først bruke cosinussetningen til å bestemme \(x\), deretter vil omkretsen av tolvkanten være \(12x\). Vi bestemmer dette med CAS:

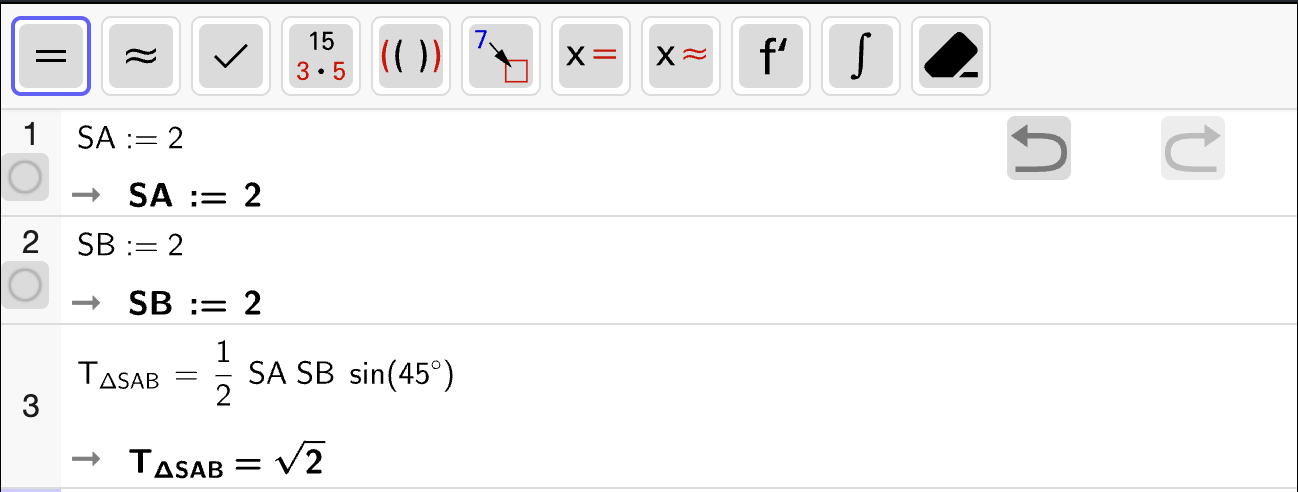
Som betyr at omkretsen av tolvkanten er

\[ \mathcal{O} = 24\left(\sqrt{15} - \sqrt{5}\right) \]

---

Oppgave 4 (5 poeng)

Ovenfor ser du tre figurer. Figurene er satt sammen av små kvadrater.
Tenk deg at du skal fortsette å lage figurer etter samme mønster.

a

Du skal lage et program som beregner og skriver ut hvor mange små fargelagte kvadrater det vil være i hver av de 20 første figurene.

Sett opp en algoritme du kan bruke for å lage programmet.

Løsning

Vi lar \(f(n)\) betegne antall små kvadrater i figur \(n\). Vi kan merke oss at antall små kvadrater i figur \(n\) vil være gitt ved:

\[ f(n) = \underbrace{n^2}_{\text{toppen}} + \underbrace{n + 1}_{\text{diagonalen}} + \underbrace{n}_{\text{vertikal kolonne}} = n^2 + 2n + 1 = (n + 1)^2. \]

Deretter bruker vi algoritmen:

• For \(n = 1, 2, \ldots, 20\):

  • Beregn \(f(n) = (n + 1)^2\)

  • Skriv ut \(f(n)\)

b

Ta utgangspunkt i algoritmen fra oppgave a) og lag programmet.

Løsning

def f(n):
    return (n + 1) ** 2

for n in range(1, 21):
    print(f"{n = } \t {f(n) = }")

som gir utskriften

n = 1 	 f(n) = 4
n = 2 	 f(n) = 9
n = 3 	 f(n) = 16
n = 4 	 f(n) = 25
n = 5 	 f(n) = 36
n = 6 	 f(n) = 49
n = 7 	 f(n) = 64
n = 8 	 f(n) = 81
n = 9 	 f(n) = 100
n = 10 	 f(n) = 121
n = 11 	 f(n) = 144
n = 12 	 f(n) = 169
n = 13 	 f(n) = 196
n = 14 	 f(n) = 225
n = 15 	 f(n) = 256
n = 16 	 f(n) = 289
n = 17 	 f(n) = 324
n = 18 	 f(n) = 361
n = 19 	 f(n) = 400
n = 20 	 f(n) = 441

c

Tenk deg at du har 1 000 000 små kvadrater. Du starter med å lage figur 1 og fortsetter så med å lage figur 2, figur 3 og så videre.

Lag et program som du kan bruke for å finne ut hvor mange figurer du kan lage, og hvor mange små kvadrater du har igjen når du har laget alle figurene.

Løsning

def f(n):
    return (n + 1) ** 2

    
antall_kvadrater = 1_000_000

for n in range(1, 10_000_000):
    # Hvis vi bruker for mange, så stopper vi
    if antall_kvadrater - f(n) < 0: 
        n = n - 1 # Vi får ikke lagde denne figuren, så vi tar bort 1
        break
    
    # Lag en ny figur og trekk fra kvadratene
    antall_kvadrater = antall_kvadrater - f(n)


print(n, antall_kvadrater)

som gir utskriften

142 15017

Dermed kan vi lage 142 figurer, og da har vi 15 017 kvadrater igjen.

---

Oppgave 5 (6 poeng)

Isabel er industridesigner. Hun arbeider med et design på bokser med form som sylindre.

Opplysninger

Formel for å regne ut volumet av en boks med radius \(r\) og høyde \(h\) er

\[ V = \pi \cdot r^2 \cdot h \]

Formel for å regne ut arealet av overflaten av boksen er

\[ O = \pi \cdot r^2 + 2\cdot \pi \cdot r \cdot h \]

Isabel lurer på hvor stor radius hun bør velge og hvor høye boksene må være, når hver boks skal ha

• et volum \(V\) på \(450 \, \mathrm{cm}^3\)

• minst mulige overflate \(O\)

Isabel ser at når hun har gitt volum og radius, kan hun regne ut høyden ved å bruke formelen \(V = \pi \cdot r^2 \cdot h\)

a

Lag en oversikt som vist nedenfor. Gjør beregninger og fyll inn verdiene som mangler.

Radius, \(r\) (cm)	Høyde, \(h\) (cm)	Overflate, \(O\) (cm\(^2\))	Volum, \(V\) (cm\(^3\))
2	35.8	462.6	450
4			450
6			450
8			450

Løsning

Vi kan skrive om formelen for volum slik at vi kan bestemme høyden \(h\) gitt et volum \(V\) og en radius \(r\) som:

\[ V = \pi \cdot r^2 \cdot h \liff h = \dfrac{V}{\pi \cdot r^2} \]

Deretter lager vi et regneark der vi fyller ut tabellen:

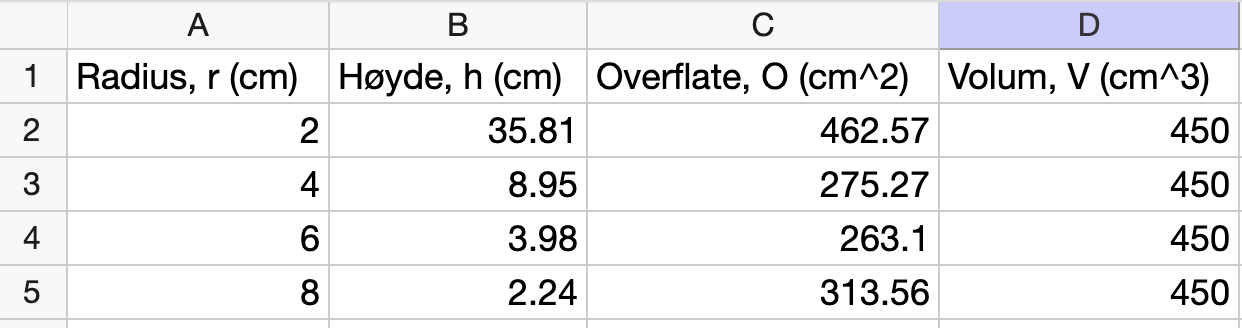
Nedenfor vises en oversikt over formlene som er brukt i regnearket:

b

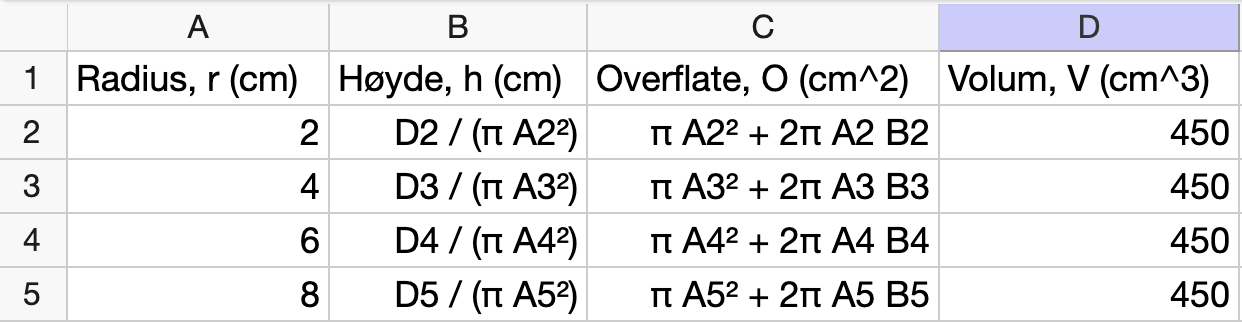
Sett opp et funksjonsuttrykk Isabel kan bruke, og lag en grafisk framstilling som viser sammenhengen mellom radius og overflate.

Løsning

Vi kan lage et funksjonsuttrykk \(O(r)\) for overflaten \(O\) av boksen for en gitt høyde \(r\). Volumet \(V = 450\), så vi kan sette opp et likningssystem for å bestemme \(O(r)\). Vi løser likningssystemet med CAS:

som betyr at vi kan skrive

\[ O(r) = \dfrac{\pi r^3 + 900}{r} \and h = \dfrac{450}{\pi r^2}. \]

Deretter kan vi lage en grafisk framstilling av funksjonen \(O(r)\):

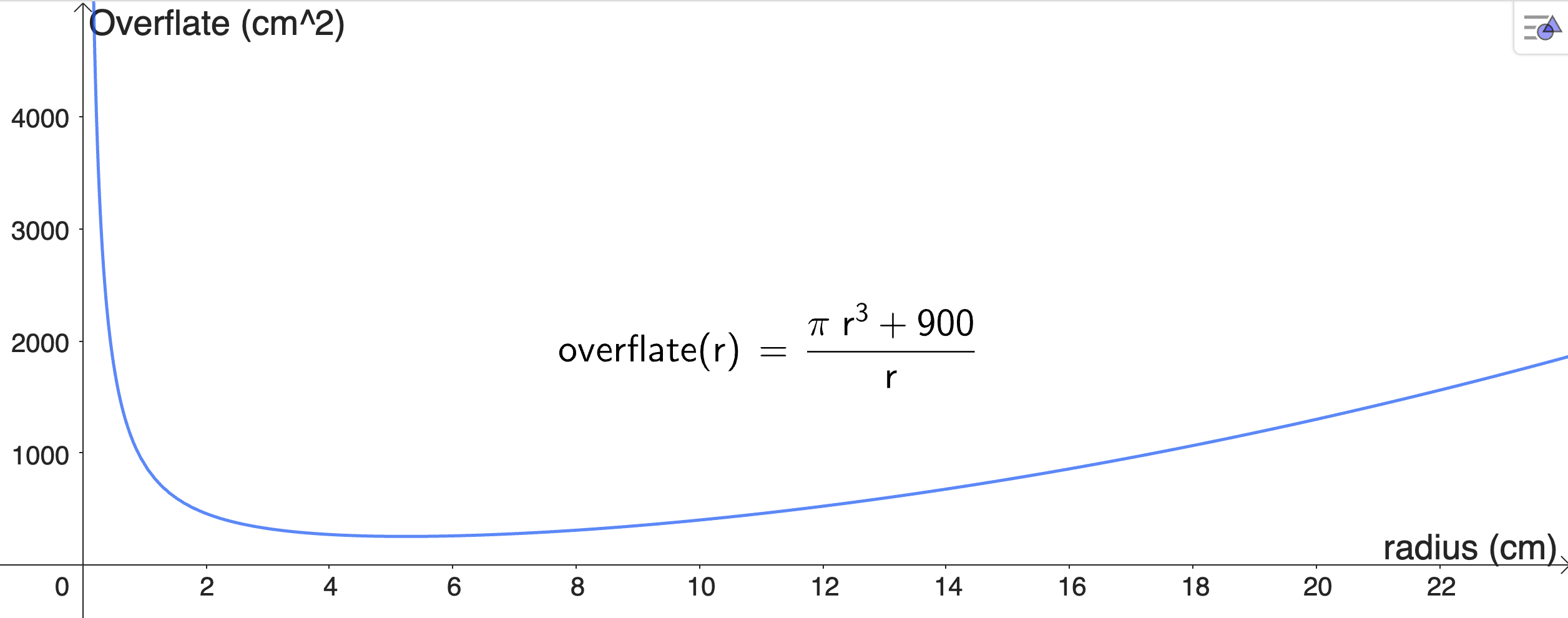
Fig. 19 viser grafen til \(O\). Her vi kalt funksjonen for overflate siden \(O\) er en innebygd funksjon i CAS-verktøyet som ikke lar seg overskrive.

c

Hvor står må radius i boksene være for at overflaten skal bli minst mulig?
Hvor stor blir overflaten da?

Løsning

For å bestemme hvilken radius som gir minst mulig overflate, så kan vi løse likningen

\[ O'(r) = 0 \]

Deretter kan vi regne ut \(O(r)\) i dette punktet. Vi gjør dette med CAS:

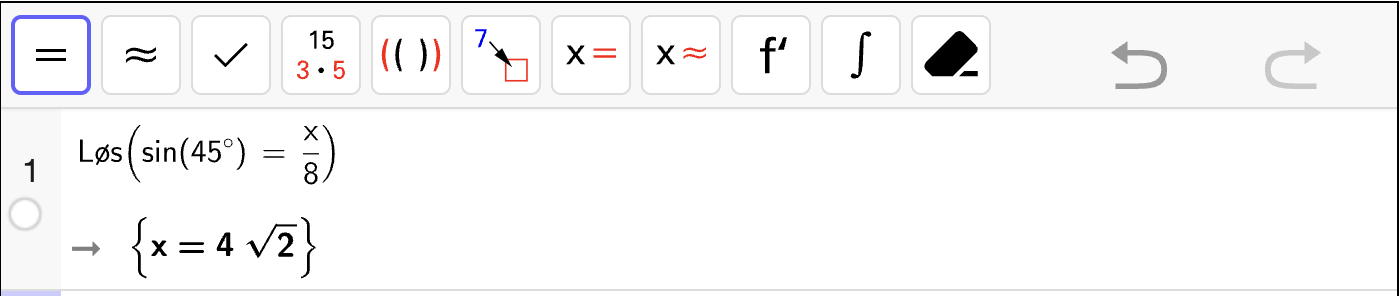
Ut ifra den grafiske framstillingen fra b kan vi være sikre på at løsningen her gir et bunnpunkt og dermed den minste overflaten. Vi har da at boksen har minst overflate dersom

\[ r \approx 5.23 \, \mathrm{cm} \]

som gir en overflate på ca. \(258 \, \mathrm{cm}^2\).

---

Oppgave 6 (4 poeng)

Klassen til Noah og Johanne arbeider med rasjonale funksjoner. Læreren har tegnet grafene til to rasjonale funksjoner \(f\) og \(g\) og bedt elevene undersøke hvordan funksjonsuttrykkene kan se ut.

Noah

Grafen til \(f\) har to vertikale asymptoter. Hvordan må nevneren i brøken da se ut?

Johanne

Jeg tror jeg vet det! Tenk på hvordan vi har funnet den vertikale asymptoten til de rasjonale funksjonene vi har arbeidet med tidligere.

Noah

Ja! Da skjønner jeg også hvordan nevneren til \(g\) kan se ut! Den grafen har jo ingen vertikale asymptoter.

Johanne

Vi må passe på at nullpunktet, skjæringspunktet med \(y\)-aksen og den horisontale asymptoten også blir riktig.

Hjelp Noah og Johanne med å finne fram til et mulig funksjonsuttrykk \(f(x)\) for funksjonen \(f\) og et mulig funksjonsuttrykk \(g(x)\) for funksjonen \(g\).

Husk å argumentere for dine valg av funksjonsuttrykk.

Løsning

En rasjonal funksjon \(f\) kan skrives på formen

\[ f(x) = \dfrac{P(x)}{Q(x)} \]

der \(P(x)\) og \(Q(x)\) er polynomer. For at grafen til \(f\) skal ha to vertikale asymptoter, må nevneren \(Q(x)\) ha to nullpunkter. Disse skal være symmetrisk fordelt om \(y\)-aksen, som betyr at \(Q(x)\) kan ha formen

\[ Q(x) = (x - a)(x + a) = x^2 - a^2 \]

for en konstant \(a > 0\). Vi kan for eksempel her velge \(a = 2\) som gir \(Q(x) = x^2 - 4\). I tillegg er likningen for den horisontale asymptoten til \(f\) gitt ved \(y = 0\) siden den horisontale asymptoten samsvarer med \(x\)-aksen. For å oppnå dette må grafen til nevenerpolynomet være minst én grad høyere enn graden til tellerpolynomet. Dermed kan \(P(x)\) høyest være av grad \(1\). Siden grafen til \(f\) også skjærer \(x\)-aksen, må \(P(x)\) ha ett nullpunkt og derfor være et polynom av grad \(1\). Nullpunktet er positivt, men ligger mellom de to vertikale asymptotene som betyr at et mulig valg for \(P(x)\) kan være

\[ P(x) = x - 1. \]

Nå trenger vi bare å sjekke at \(f(0) > 0\) siden grafen til \(f\) skjærer \(y\)-aksen i et punkt der \(y > 0\). Vi har

\[ f(x) = \dfrac{x - 1}{x^2 - 4} \limplies f(0) = \dfrac{0 - 1}{0^2 - 4} = \dfrac{-1}{-4} = \dfrac{1}{4} > 0. \]

Dermed har vi funnet et mulig funksjonsuttrykk \(f(x)\) for funksjonen \(f\).

For grafen til \(g\) må vi sørge for at den ikke har noen vertikale asymptoter, som vi kan oppnå ved å velge en nevner som ikke har noen nullpunkter. Siden grafen også har en horisontal asymptote med likning \(y = 0\), og et nullpunkt \(x < 0\), så kan vi velge at tellerpolynomet er av grad \(1\) og nevnerpolynomet er av grad \(2\) og har ingen nullpunkter. Ett mulig valg som tilfredsstiller disse kravene er

\[ P(x) = x + 1 \and Q(x) = x^2 + 1. \]

Her får vi et nullpunkt i \(x = -1\), ingen vertikale asymptoter og en horisontal asymptote med likning \(y = 0\). Vi må igjen sjekke at grafen til \(g\) vi skjærer \(y\)-aksen i et punkt der \(y > 0\):

\[ g(x) = \dfrac{x + 1}{x^2 + 1} \limplies g(0) = \dfrac{0 + 1}{0^2 + 1} = \dfrac{1}{1} = 1 > 0. \]

Altså tilfredsstiller vi alle kravene til grafen til \(g\) og vi har funnet et mulig funksjonsuttrykk \(g(x)\) for funksjonen \(g\).

Vi kan lage en grafisk framstilling av de to funksjonene for å være sikker på at de stemmer overens med grafene i oppgaven:

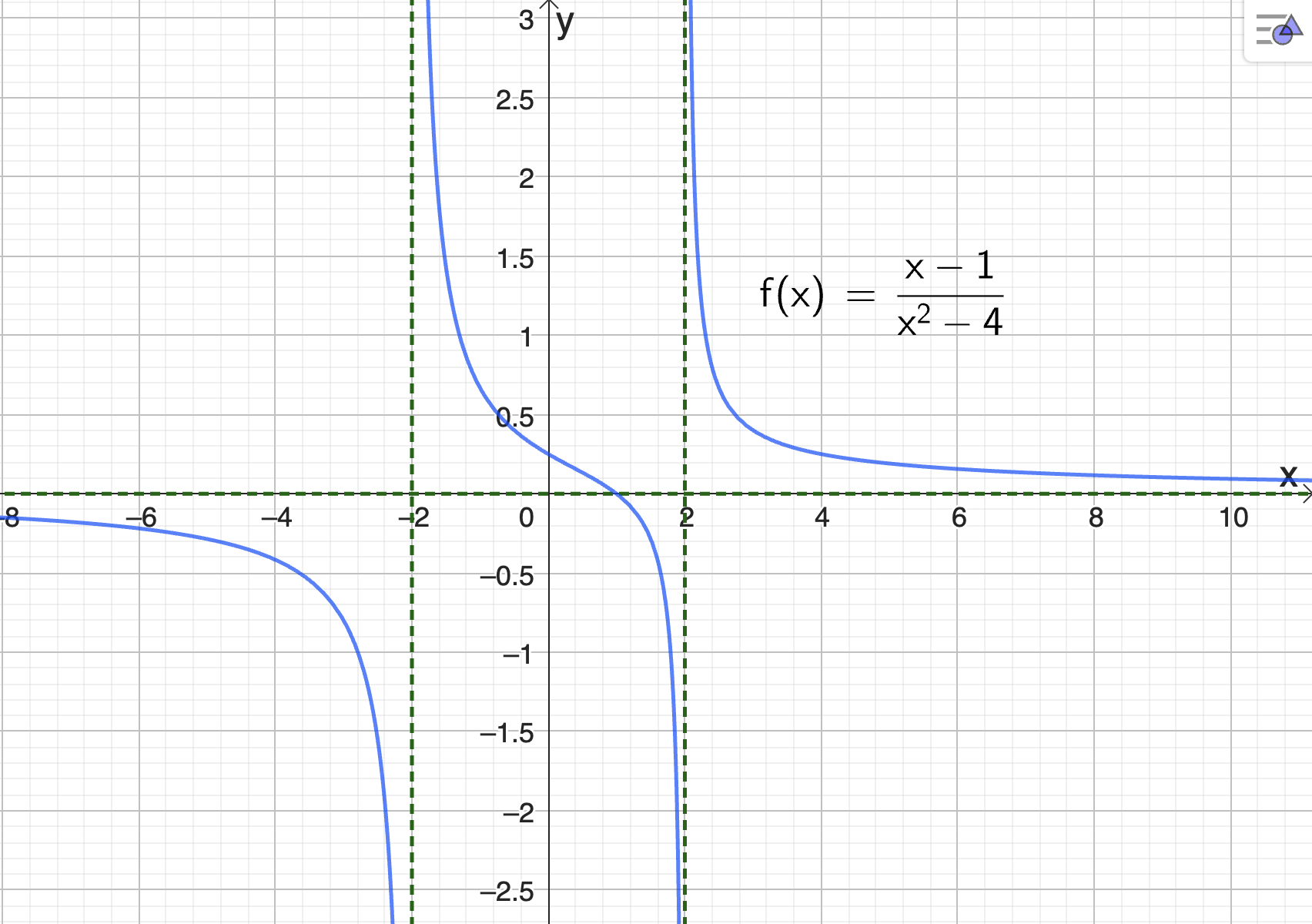
Fig. 20 viser grafen til \(f\).

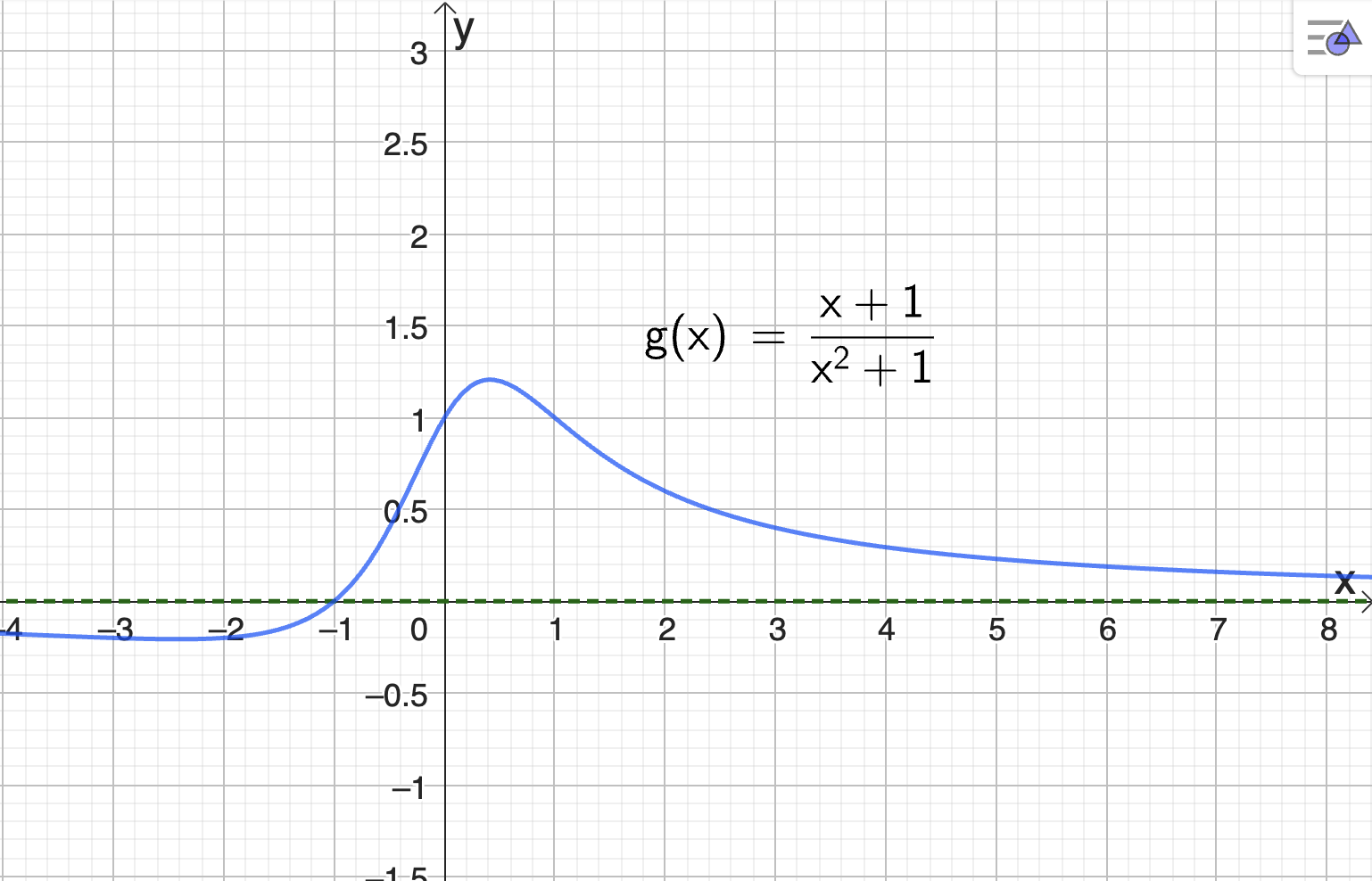
Fig. 21 viser grafen til \(g\).