Funksjoner (Del 2)#
Her kan du bruke digitale hjelpemidler som CAS, graftegner (Geogebra), Python og regneark til å løse oppgaver.
Oppgave 1 (Vår 2024)
Den rette linjen som er tegnet i koordinatsystemet ovenfor, er den deriverte av en funksjon \(f\).
Punktet \(P(1, 2)\) ligger på grafen til \(f\).
Bestem likningen for tangenten til grafen til \(f\) i punktet \(P\).
Husk å argumentere for at svaret ditt er riktig.
Fasit
Løsning
Siden \(P(1, 2) \in f\), så er \(f(1) = 2\). Siden \(x\)-koordinaten er \(x = 1\), betyr det stigningstallet til tangenten er \(a = f'(1)\). Fra grafen til \(f'\) ovenfor, kan vi se at grafen går gjennom punktet \((1, -2)\) som betyr at \(f'(1) = -2\).
Bruker vi ettpunktsformelen, blir derfor likningen for tangenten til \(f\) i punktet \(P\) gitt ved
Oppgave 2 (Høst 2024)
En rasjonal funksjon \(f\) har asymptotene \(x = 2\) og \(y = 4\).
Nullpunktet til funksjonen er \(x = -3\).
Bestem et mulig funksjonsuttrykk \(f(x)\).
Gjør rede for hvordan du har tenkt for å komme fram til funksjonsuttrykket.
Fasit
Løsning
Ut ifra opplysningene kan vi skrive om en rasjonal funksjon på formen
der
\(y = a\) er \(f\) sin horisontale asymptote
\(x = c\) er \(f\) sin vertikale asymptote
\(x = -b\) er \(f\) sitt nullpunkt
Fra opplysningene har vi at
\(a = 4\) fordi \(y = 4\) er den horisontale asymptoten
\(b = -3\) fordi \(x = -3\) er nullpunktet
\(c = 2\) fordi \(x = 2\) er den vertikale asymptoten
Dermed er et mulig funksjonsuttrykk \(f(x)\) gitt ved
Oppgave 3 (Høst 2024)
Du får vite følgende om en tredjegradsfunksjon \(f\) gitt ved
Grafen til \(f\) går gjennom punktet \((2, 6)\).
Punktet \((-2, 8)\) er et toppunkt på grafen til \(f\).
Tangenten til grafen til \(f\) i punktet \((3, f(3))\) har stigningstall \(4\).
Bruk opplysningene ovenfor til å bestemme \(a\), \(b\), \(c\) og \(d\).
Fasit
Løsning
Fra opplysningene kan vi sette opp et likningssystem med fire likninger og fire ukjente.
Grafen til \(f\) går gjennom punktet \((2, 6)\)
Fra dette kan vi sette opp likningen
Punktet \((-2, 8)\) er et toppunkt på grafen til \(f\)
Fra dette kan vi sette opp to likninger:
Tangenten til grafen til \(f\) i punktet \((3, f(3))\) har stigningstall \(4\)
Stigningstallet til tangenten er lik den deriverte i punktet \(x = 3\), så vi kan skrive
Nå har vi likningssystemet
Vi løser likningssystemet med CAS:

Altså har vi at
Oppgave 4 (Høst 2023)
Ovenfor har sara tegnet grafene til funksjonene \(f\) og \(g\) gitt ved
Linjen \(x = 1\) skjærer grafen til \(f\) i punktet \(P\) og grafen til \(g\) i punktet \(Q\).
Bestem avstanden fra \(P\) til \(Q\).
Fasit
Løsning
La \(PQ\) være avstanden fra \(P\) til \(Q\). Siden \(x\)-koordinaten til de to punktene er like, følger det at avnstanden \(PQ\) er lik avstanden mellom \(y\)-koordinatene til punktene \(P\) og \(Q\). Altså blir avstanden:
Vi regner ut avstanden med CAS:
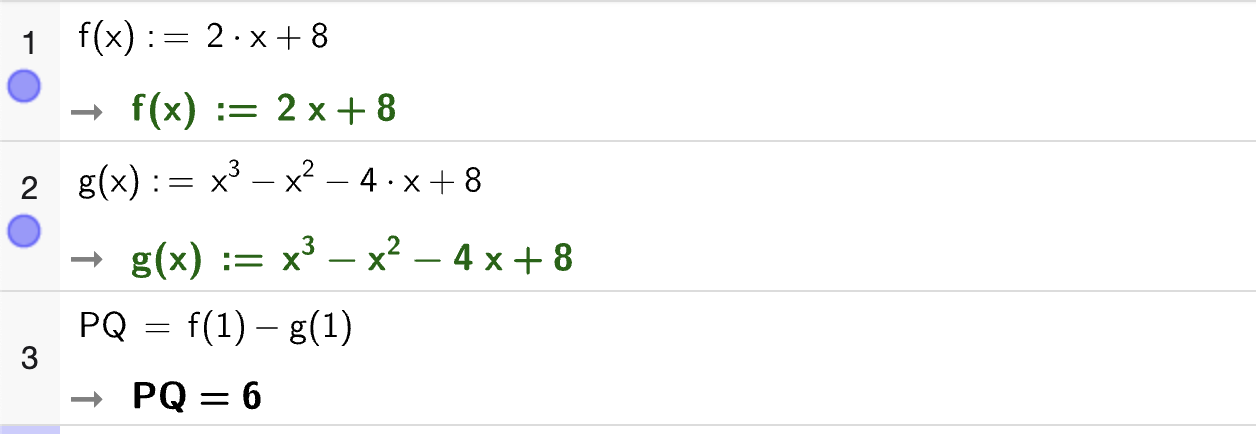
Altså er avstanden fra \(P\) til \(Q\) gitt ved \(PQ = 6\).
Sara skal tegne en ny linje \(x = a\) der \(a \in \langle 1, 3 \rangle\) i koordinatsystemet.
Hun vil kalle skjæringspunktet mellom linjen og grafen til \(f\) for \(R\) og skjæringspunktet mellom linjen og grafen til \(g\) for \(S\).
Bestem \(a\) slik at avstanden fra \(R\) til \(S\) blir størst mulig. Oppgi svaret eksakt.
Fasit
Løsning
La \(d(a)\) være avstanden fra \(R\) til \(S\). Da har vi at
For å bestemme hvilken verdi av \(a\) som gir størst mulig avstand, kan vi bruke CAS til å løse \(d'(a) = 0\) for \(a \in \langle 1, 3 \rangle\):
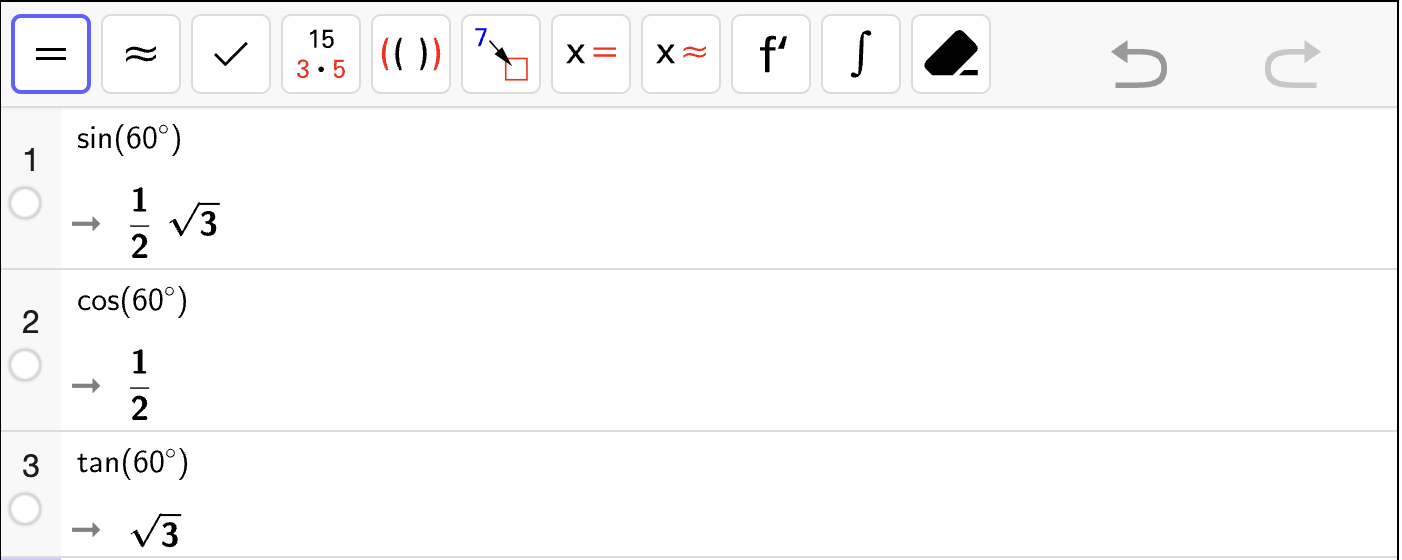
Fig. 9 Merk at definisjonene av \(f(x)\) og \(g(x)\) ligger igjen fra oppgave a.#
Vi finner altså at
gir størst mulig avstand mellom \(R\) og \(S\). Vi kan være sikre på at dette er den riktige verdien for \(a\) ved å sjekke \(d(a)\) i endepunktene og sjekke at verdiene er lavere enn \(d(a)\) i \(a_\mathrm{størst}\):

Ja. Vi legger’n død.
Oppgave 5 (Høst 2023)
En tredjegradsfunksjon \(f\) er gitt ved
Punktet \((-8, 0)\) er et toppunkt på grafen til \(f\).
Den gjennomsnittlige vekstfarten til \(f\) i intervallet \([0, 5]\) er \(\dfrac{64}{5}\).
Bestem \(a\), \(b\) og \(c\).
Fasit
Løsning
Vi kan sette opp et likningssystem med tre likninger og tre ukjente fra opplysningene i oppgaven.
Punktet \((-8, 0)\) er et toppunkt på grafen til \(f\)
Fra dette kan vi sette opp to likninger:
Den gjennomsnittlige vekstfarten til \(f\) i intervallet \([0, 5]\) er \(\dfrac{64}{5}\)
Fra dette kan vi sette opp likningen
Vi løser likningssystemet med CAS:

som betyr at
Oppgave 6 (Vår 2022)
Grafen til en andregradsfunksjon \(f\) har
en tangent i punktet \((1, f(1))\) med stigningstall \(0\).
en tangent i punktet \((4, f(4))\) med stigningstall \(6\).
Bestem \(f'(x)\).
Fasit
Løsning
Siden \(f\) er en andregradsfunksjon, kan vi skrive den på formen
Fra opplysningene i oppgaven kan vi sette opp to likninger for de to ukjente koeffisientene \(a\) og \(b\):
Likningene følger fra at stigningstallet til tangentene er lik den deriverte i de aktuelle punktene. Vi løser likningssystemet med CAS:
som betyr at
Grafen til \(f\) skjærer \(y\)-aksen i punktet \((0, 4)\).
Bestem \(f(x)\).
Fasit
Løsning
Fra oppgave a vet vi at
Siden vi nå vet at grafen til \(f\) skjærer \(y\)-aksen i punktet \((0, 4)\), følger det at
Dermed er
Oppgave 7 (Høst 2024)
Else skal gjerde inn tre områder for å lage en grønnsakshage. Det største området skal ha form som et rektangel og de to minste som likebeinte rettvinklede trekanter. Se figuren ovenfor.
Else skal sette opp gjerde langs alle linjestykkene vist i figuren ovenfor.
Hun har til sammen 100 m gjerde som hun vil bruke.
Hvor stor blir arealet av grønnsakhagen dersom hun velger at katetene i trekantene skal være \(8\) meter?
Fasit
Løsning
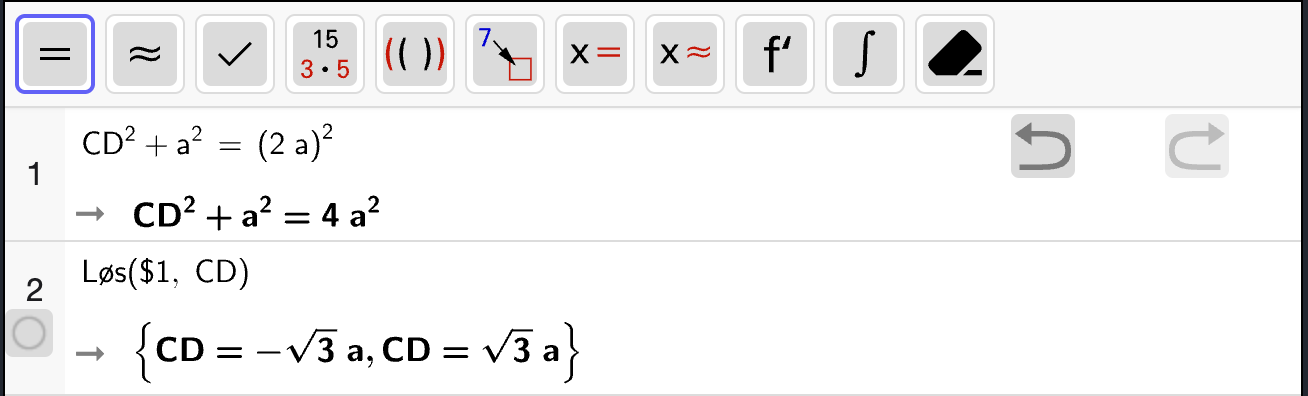
Først må vi bestemme hvor lange linjestykkene \(y\) i figuren er. Vi vet at \(x = 8\) meter. Til sammen summerer linjestykkene til \(L = 100\) meter. Vi kan skrive den samlede lengden av linjestykkene som
der vi har brukt Pytagoras’ setning til å finne at begge hypotenusene i de rettvinklede trekantene må være
Vi kan først løse likningen for \(y\) slik at vi kan regne ut \(y\) for en hver verdi av \(x\):
som gir
Det samlede arealet til grønnsakhagen blir
Vi kan definere en funksjon \(A(x)\) i CAS og regne ut arealet for \(x = 8\):
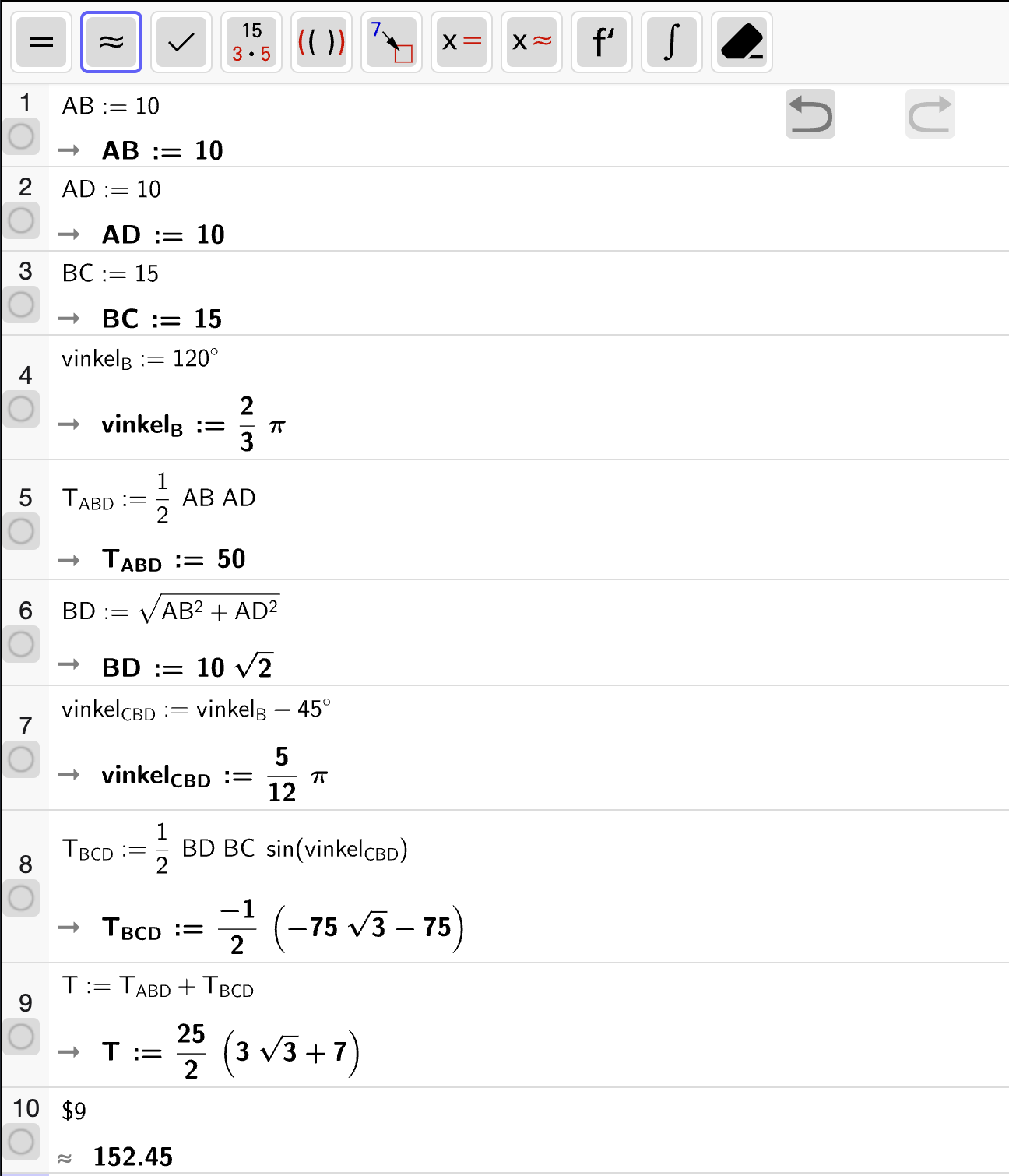
som betyr at arealet av grønnsakhagen er omtrent \(A = 245.5 \, \mathrm{m}^2\) dersom katetene i trekantene er \(8\) meter lange.
Lag en oversikt som viser hvordan arealet av grønnsakhagen endrer seg dersom hun velger andre lengder på katetene. Av oversikten skal Else kunne se omtrent hvor lange katetene må være for at arealet av grønnsakhagen skal bli størst mulig.
Løsning
Vi bruker en grafisk framstilling av arealet \(A(x)\) for å se hvordan arealet endrer seg med lengden på katetene. Vi kan bruke Geogebra-vinduet til å lage grafen til \(A\) siden vi allerede har definert \(A(x)\) i CAS.
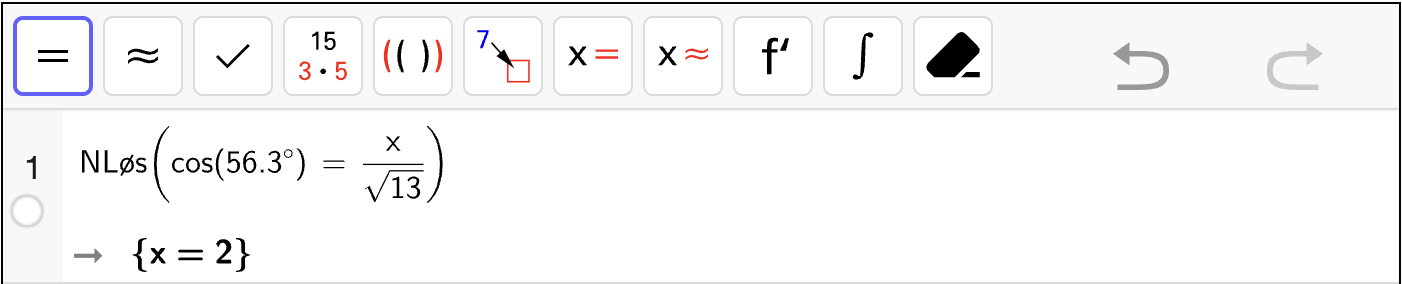
Fig. 10 viser en grafisk fremstilling av arealet \(A(x) \, \mathrm{m}^2\) på \(y\)-aksen når katetene i trekanten er \(x\) meter lange.#
Fra den grafiske framstillingen kan vi se at arealet er størst når katetene i trekanten er omtrent \(x = 10\) meter lange fordi dette svarer til et toppunkt på grafen til \(A\).
Lag en modell \(A\) som Else kan bruke for å regne ut arealet \(A(x)\) av grønnsakhagen for ulike verdier av \(x\).
Fasit
Løsning
Vi har allerede laget denne modellen i oppgave a som er gitt ved
Bruk modellen til å finne den lengden av katetene som vil gi det største arealet.
Fasit
Løsning
For å bestemme den kateten som gir størst mulig areal, bruker vi CAS og løser \(A'(x) = 0\) for å bestemme \(x\)-koordinaten til toppunktet til \(A\):
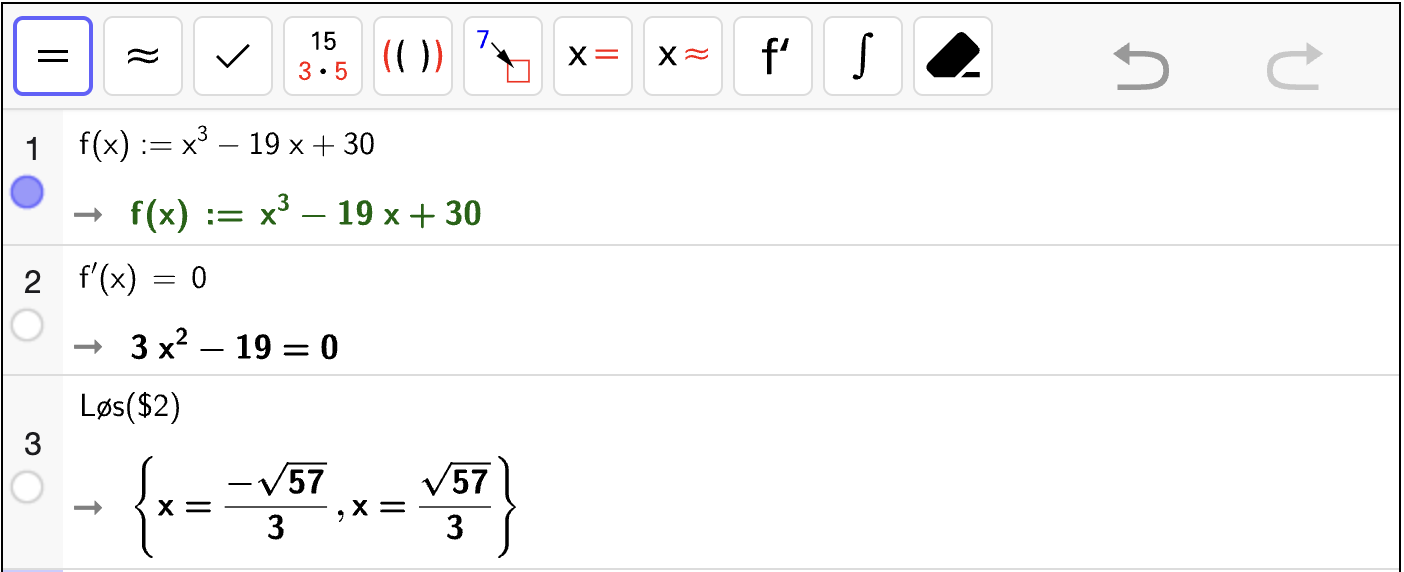
som betyr at arealet er størst når katetene i trekantene er
Men vet vi at dette er et toppunkt? Ja, for den ledende koeffisienten til \(A(x)\) er negativ, så vi legger’n død – og vi hadde strengt tatt grafen som viste det i oppgave b også.
Bestem modellens gyldighetsområde.
Fasit
Løsning
Modellen er gyldig så lenge \(A(x) > 0\) og \(y > 0\). Vi løser den første ulikheten i CAS:

Altså er \(A(x) > 0\) når
Men vi må også sjekke at \(y > 0\). Fra a vet vi at
så vi løser ulikheten \(y > 0\) i CAS:

Kombinerer vi de to løsningene, ser vi at modellen er gyldig så lenge
Oppgave 8 (Vår 2022)
Funksjonen \(f\) er gitt ved
Vis at \(f\) bare har ett nullpunkt uavhengig av verdien av \(b\).
Løsning
Vi bestemmer nullpunktene til \(f\) ved å løse likningen \(f(x) = 0\) med CAS:
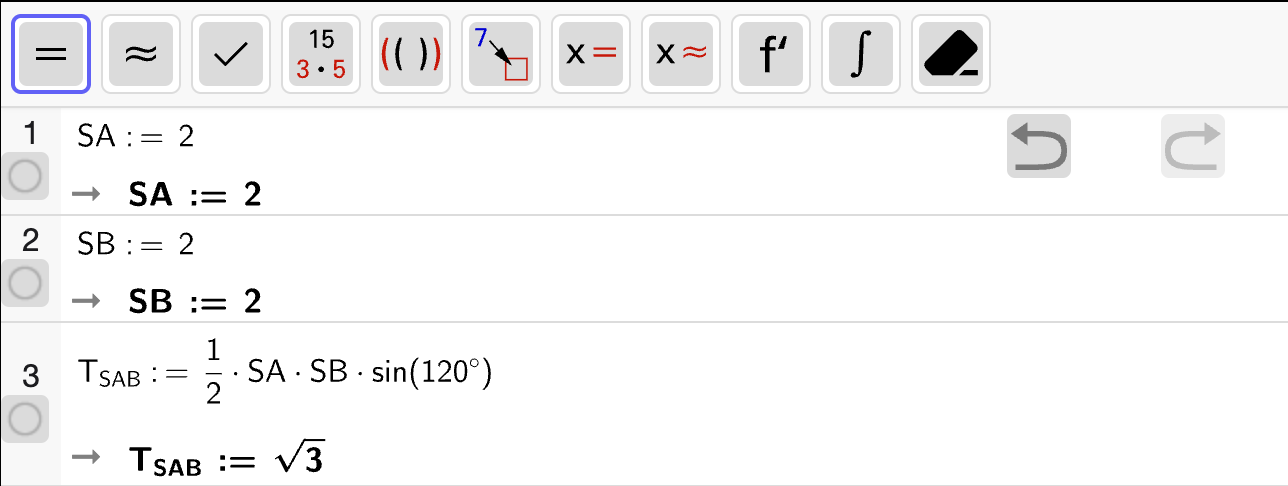
Altså ser vi at
Denne løsningen er ikke avhengig av verdien til \(b\), for da måtte \(b\) ha dukket opp som en del av løsningen. Dermed har \(f\) bare ett nullpunkt uavhengig av verdien til \(b\), og dette nullpunktet er \(x = 0\).
Løs likningen \(f'(x) = 0\).
For hvilke verdier av \(b\) har grafen til \(f\) bare ett stasjonært punkt?
Et stasjonært punkt er et punkt der den deriverte er lik null.
Fasit
Dersom \(b \neq 0\) har grafen til \(f\) to tangenter med stigningstall \(3\).
Bestem likningene for disse tangentene.
Fasit
Tangenten i punktet* \((b, f(b))\) er \(y = 3x\)
Tangenten i punktet \(\left(\dfrac{1}{3}b, f\left(\dfrac{1}{3}b\right)\right)\) er \(y = 3x + \dfrac{4}{27}b^3\).
Løsning
Vi løser likningen \(f'(x) = 3\) med CAS for å bestemme ved hvilke \(x\)-verdier vi får tangenter som har stigningstall \(3\).
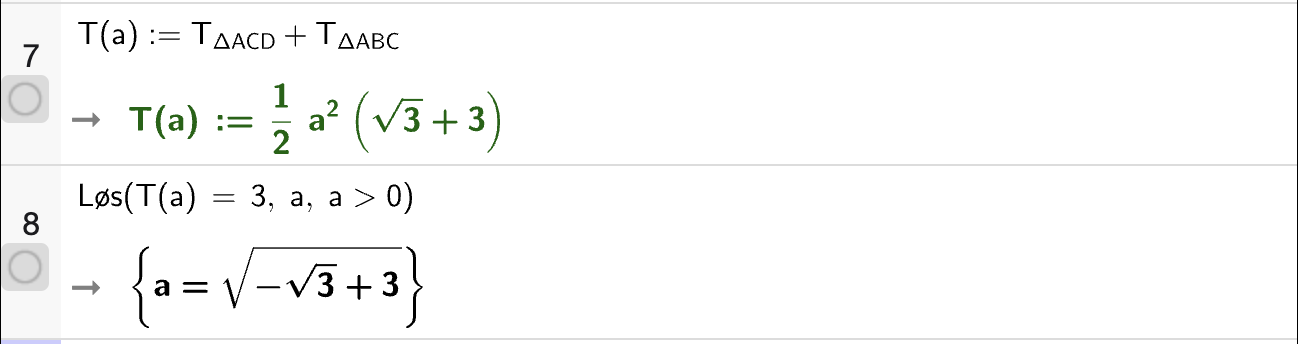
Fig. 11 viser løsningen av \(f'(x) = 3\). Vi bruker fortsatt \(f(x)\) fra oppgave a.#
Altså er
Vi bestemmer likningene for tangentene i to punktene med CAS direkte med Tangent(punkt, funksjon)-funksjonen:
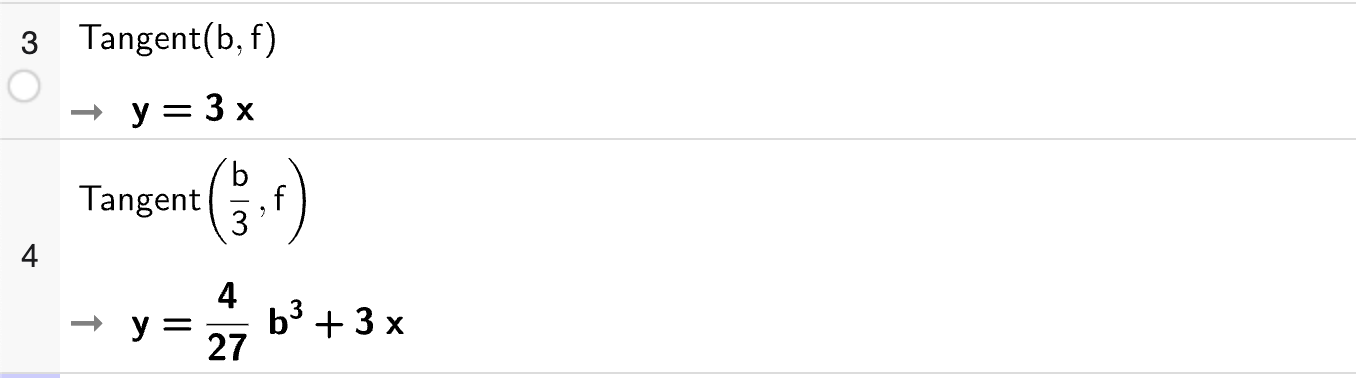
som betyr at likningen for tangenten i \(x = b\) er gitt ved
og likningen for tangenten i \(x = \dfrac{1}{3}b\) er gitt ved
Oppgave 9
Anna skal reise fra en holme som ligger \(8\) km fra strandkanten. \(12\) km fra det punktet på stranden som ligger nærmest holmen, ligger det en hytte. Se figuren nedenfor.
Anna kan ro med en fart på \(2\) km/t og gå med en fart på \(6\) km/t.
Bestem hvor lang tid Anna bruker til hytta dersom hun ror i land \(6\) km fra det punktet på stranden som ligger nærmest holmen.
Fasit
Løsning
Vi bruker Pytagoras’ setning til å regne ut hvor langt Anna må ro for å komme i land \(6\) km fra det punktet på stranden som ligger nærmest holmen. Da får vi at:
Siden Anna ror med en fart på \(2\) km/t, bruker hun tiden
til å ro til stranden. Hun må deretter gå \(12 - 6 = 6\) km til hytta. Siden hun går med en fart på \(6\) km/t, bruker hun tiden
til å gå til hytta. Den totale tiden hun bruker til hytta blir derfor
Lag en modell \(T\) som viser mange timer \(T(x)\) Anna bruker på å reise til hytta dersom hun ror i land \(x\) km fra det punktet på stranden som ligger nærmest holmen.
Fasit
Løsning
Hvis Anna ror i land \(x\) km fra det punktet på stranden som ligger nærmest holmen, må hun ro en avstand på
Anna ror med en fart på \(2\) km/t, så tiden hun bruker til å ro blir
Siden avstanden er 12 km fra punktet på strandlinja nærmest holmen bort til hytta, så må hun gå
kilometer til hytta. Anna går med en fart på \(6\) km/t, så tiden hun bruker til å gå blir
Dermed vil en modell for tiden Anna bruker til hytta når hun ror i land \(x\) km fra det punktet på stranden som ligger nærmest holmen være gitt ved
Bestem hvor Anna må gå i land for at hun skal bruke minst mulig tid på å reise til hytta.
Hva er den kortest tiden Anna kan bruke?
Fasit
Anna må gå i land ved \(x \approx 2.83 \, \mathrm{km}\) for å få kortest mulig reisetid.
Anna bruker da \(T \approx 5.77 \, \mathrm{t}\) på reisen.
Løsning
For å finne ut hvor Anna må gå i land for at hun skal bruke minst mulig tid på å reise til hytta, løser vi likningen \(T'(x) = 0\) med CAS for å finne \(x\)-koordinaten til et eventuelt bunnpunkt for \(T\):
Dermed vil Anna bruke minst mulig tid dersom hun går i land ved
Da bruker hun ca. \(5.77\) timer på reisen.
Vi bør dobbeltsjekke at dette svarer til et bunnpunkt ved å regne ut \(T(x)\) i endepunktene og sjekke at verdiene vi får er høyere:

Hvis Anna ror båten direkte til nærmeste punkt på stranden, bruker hun \(T(0) = 6\) timer.
Hvis Anna ror båten hele veien til hytta, bruker hun \(T(12) \approx 7.21\) timer.
Konklusjon:
Anna må gå i land ved \(x \approx 2.83 \, \mathrm{km}\) for å få kortest mulig reisetid.
Anna bruker da \(T \approx 5.77 \, \mathrm{t}\) på reisen.
Oppgave 10 (Høst 2023)
Nedenfor ser du grafen til funksjon \(f\) gitt ved
Rektangelet under grafen har hjørner i punktene \((0, 0)\), \((5, 0)\), \((5, f(5))\) og \((0, f(5))\).
Bestem arealet av rektangelet.
Lag en systematisk oversikt som viser arealet av rektanglene som har hjørner i punktene \((0, 0)\), \((n, 0)\), \((n, f(n))\) og \((0, f(n))\) for \(n \in \{1, 2, 3, \ldots, 10\}\).
Løsning
Her er det mange muligheten for hva som menes med “systematisk oversikt”. Vi velger å lage en grafisk framstilling, men man kan for eksempel lage en verditabell ved hjelp av en Pythonprogram eller regne ut verdiene med CAS og lage en tabell manuelt.
Vi kan lage en modell \(A\) for arealet av rektangelet, og så vise en graf av arealet der vi marker punktene \((n, A(n))\) for \(n \in \{1, 2, 3, \ldots, 10\}\) på grafen. Modellen \(A(x)\) vil være
Vi tegner grafen til \(A\) med en graftegner og markerer punktene \((n, A(n))\) for \(n \in \{1, 2, 3, \ldots, 10\}\):
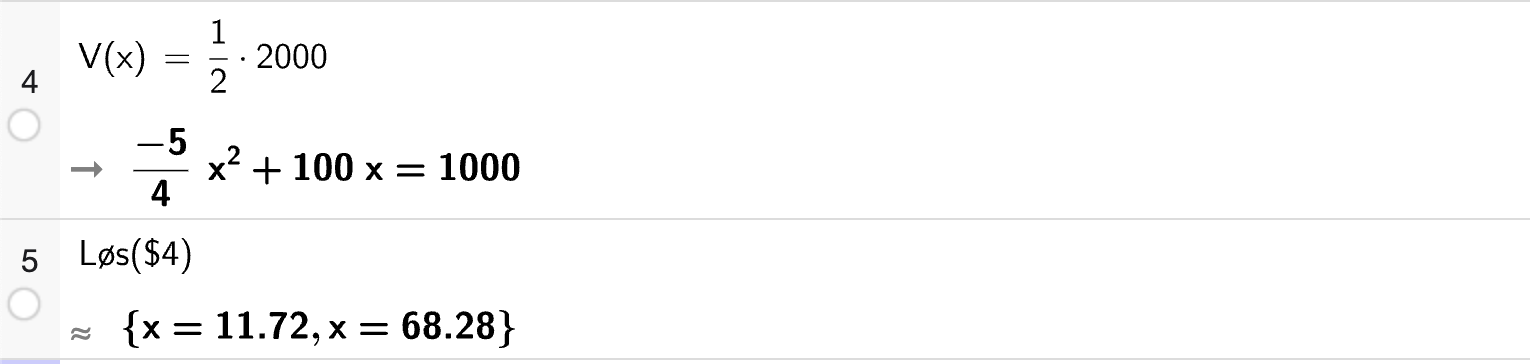
Fig. 12 viser grafen til arealet \(A\) med punktene \((n, A(n))\) for \(n \in \{1, 2, 3, \ldots, 10\}\) markert med koordinater. Her viser \(y\)-aksen arealet \(A(x)\).#
Bestem \(k\) slik at arealet av rektangelet som har hjørner i punktene \((0, 0)\), \((k, 0)\), \((k, f(k))\) og \((0, f(k))\) blir størst mulig.
Løsning
For å bestemme hvilke verdi av \(k\) som gir størst mulig areal, kan vi løse likningen \(A'(k) = 0\) med CAS:

Den eneste kandidaten for \(k\) som gir mening er \(k = 2\sqrt{5}\) siden dette er den eneste verdien av \(k\) der \(k > 0\). At
gir størst mulig areal stemmer bra med oversikten vi lagde i oppgave b der vi kan se fra grafen at toppunktet må ligge mellom \(x = 4\) og \(x = 5\). Dermed vil \(k = 2\sqrt{5}\) gi størst mulig areal av rektangelet.
Oppgave 11 (Høst 2021)
Skissen ovenfor viser grafen til funksjonen \(f\) gitt ved \(f(x) = \dfrac{1}{x}\) og tangenten til grafen i punktet \((s, f(s))\).
Vis at likningen for tangenten er
Tangenten skjærer koordinataksene i punktene \(A\) og \(B\).
Bestem koordinatene til \(A\) og \(B\) uttrykt ved \(s\).
Fasit
Løsning
Vi kaller tangenten for \(T\). Da vil skjæringen med \(y\)-aksen svaret til \(T(0)\) og skjæringen med \(x\)-aksen svarer til løsningen av \(T(x) = 0\). Vi regner ut begge disse verdiene med CAS:

Fra celle 3, kan vi lese av at punktet \(B\) kan skrives som
Og fra celle 4 kan vi lese av at punktet \(A\) kan skrives som
Bestem arealet av \(\triangle OAB\).
Fasit
Arealet av \(\triangle OAB\) er gitt ved
Løsning
\(OA\) er grunnlinjen i trekanten og \(OB\) er høyden. Arealet av trekanten er da:
Oppgave 12 (Eksempelsett 2021)
En funksjon \(f\) er gitt ved
Grafen til \(f\) har to tangenter som er parallelle med linjen \(y = \dfrac{1}{2}x + 2\).
Bestem en eksakt verdi for nullpunktet til hver av disse tangentene.
Fasit
Tangenten i punktet \(\left(-\dfrac{\sqrt{2}}{2}, f\left(-\dfrac{\sqrt{2}}{2}\right)\right)\) har nullpunktet
og tangenten i punktet \(\left(\dfrac{\sqrt{2}}{2}, f\left(\dfrac{\sqrt{2}}{2}\right)\right)\) har nullpunktet
Løsning
Tangentene vil ha stigningstall \(\dfrac{1}{2}\) siden de er parallelle med linjen \(y = \dfrac{1}{2}x + 2\). Det betyr at tangentene må gå gjennom punkter på grafen til \(f\) der
Vi løser likningen med CAS for å avgjøre hvilke to punkter tangentene går gjennom:

Altså må tangentene gå gjennom to punkter på grafen til \(f\) der
Vi bruker så tangent-funksjonen i CAS til å bestemme likningene for de to tangentene og deres nullpunkter:
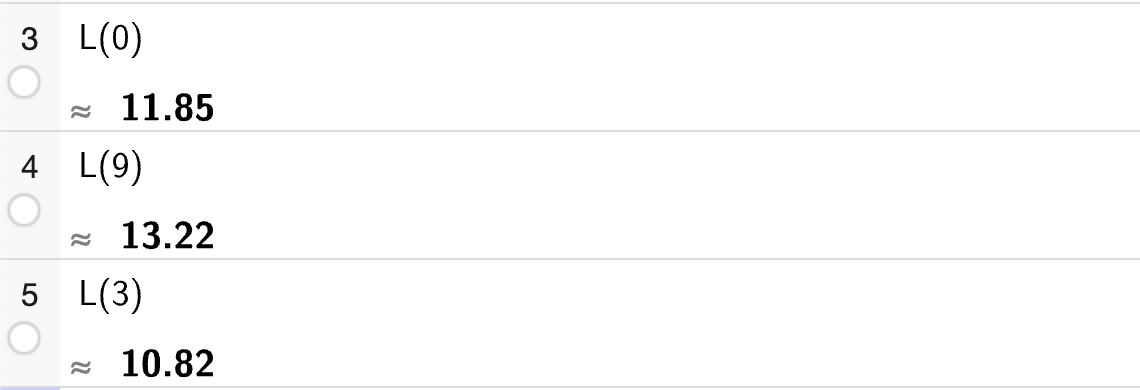
Dermed kan vi se at den ene tangenten har nullpunkt i \(x = -\sqrt{2} + 2\) og den andre tangenten har nullpunkt i \(x = \sqrt{2} + 2\).
Oppgave 13 (Eksempelsett 2021)
Figuren ovenfor viser grafen til en tredjegradsfunksjon \(f\).
Figuren viser også tangenten til grafen i tre ulike punkter.
Bruk tangentene til å bestemme et eksakt uttrykk for den deriverte funksjonen \(f'\).
Fasit
Løsning
Den deriverte funksjonen \(f'\) er en andregradsfunksjon som vi kan skrive på formen
Fra tangentene i grafen kan vi se at det er en tangent med stigningstall \(0\) i \(x = -1\) og \(x = 1\) som betyr at
Videre har vi en tangent som går gjennom \((0, 4)\) på grafen og samtidig går gjennom et annet punkt \((1, 1)\) som ikke er på grafen. Stigningstallet til denne tangenten blir da \(-3\). Siden tangenten går gjennom grafen i \(x = 0\), så vet vi derfor at den deriverte også oppfyller
Siden \(f'\) er en andregradsfunksjon med nullpunkter i \(x = -1\) og \(x = 1\), så kan vi skrive opp \(f'(x)\) på formen
Videre kan vi bruke at \(f'(0) = -3\) til å bestemme \(a\):
Dermed er
En annen måte å uttrykke \(f'(x)\) på er \(f'(x) = 3x^2 - 3\) (standardform/ekstremalpunktsform). Spiller ingen rolle hvilken vi velger å bruke.
Oppgave 14
En takrenne skal lages i form av et åpent trapes ved å brette to sidekanter fra et flatt rektangel med en vinkel \(x\) slik at alle sidelengder i takrenna er \(10\) cm.
Se figuren nedenfor.
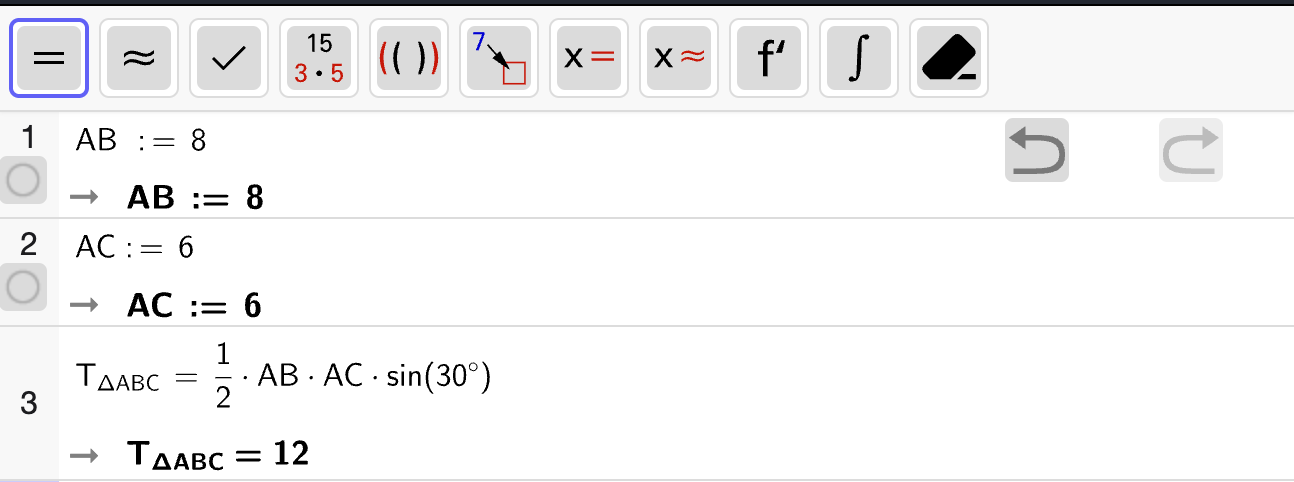
Bestem tverrsnittsarealet \(T\) av takrenna dersom vinkelen er \(30^\circ\).
Fasit
Løsning
Vi lager oss en hjelpefigur der vi tegner inn et rettvinklet trekant på hver side av trapeset og definerer en grunnlinje \(g\) og en høyde \(h\) for de to trekantene. Se figuren nedenfor.
Arealet \(T\) av figuren vil da være
For å bestemme grunnlinja \(g\) og høyden \(h\), bruker vi definisjonen av sinus og cosinus i trekantene med \(x = 30\degree\) som gir:
og
der vi har brukt at \(\sin 30\degree = \dfrac{1}{2}\) og \(\cos 30\degree = \dfrac{\sqrt{3}}{2}\). Dermed er tverrsnittsarealet \(T\) til takrenna når vinkelen er \(30\degree\) gitt ved
der \(T\) er målt i cm\(^2\).
Lag en modell \(T\) for tverrsnittsarealet \(T(x) \, \mathrm{cm}^2\) når sidekantene er brettet opp \(x\) grader.
Fasit
Løsning
Vi generaliserer regningen vi gjorde i oppgave a som betyr at
og
Dermed er en modell for tverrsnittsarealet \(T\) til takrenna når vinkelen er \(x\) grader gitt ved
Bestem hvilken vinkel som sørger for at mest mulig vann kan strømme gjennom takrenna.
Fasit
Løsning
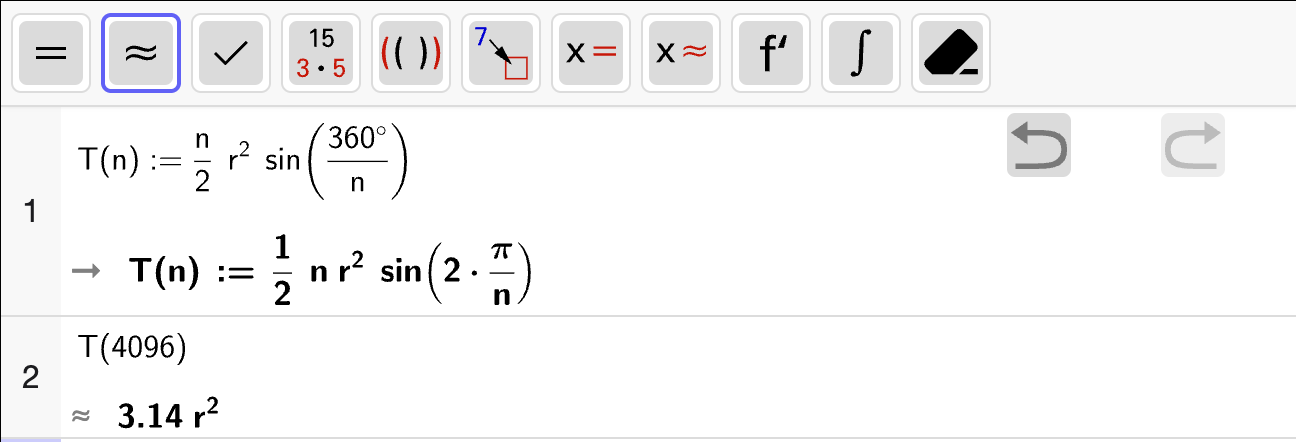
Mest mulig vann kan strømme gjennom takrenna dersom det er størst mulig tverrsnittsareal \(T(x)\). Vi kan derfor bestemme hvilken vinkel \(x\) som gir størst mulig tverrsnittsareal ved å løse likningen \(T'(x) = 0\) med CAS:

som gir \(x = 60\degree\) som den eneste løsningen. Vi bør sjekke at dette er den største verdien ved å regne ut \(T(x)\) i endepunktene \(x = 0\degree\) og \(x = 90\degree\) og sammenligne med verdien av \(T(x)\) i \(x = 60\degree\):

Fra utskriften kan vi se at \(T(60)\) er størst som betyr at \(x = 60\degree\) gir størst mulig tverrsnittsareal \(T(x)\) og dermed også lar mest mulig vann strømme gjennom takrenna.
Oppgave 15 (Høst 2022)
En bedrift produserer gardiner. Hvert gardin skal ha form som en parabel. Høyden skal være 70 cm og lengden øverst skal være 150 cm.
Se figuren til høyre.
Bedriften vil klippe ut gardinene fra tøyruller som er 140 cm brede. For å bruke så lite tøy som mulig vil en maskin klippe ut gardinene slik figuren nedenfor viser.
Gjør beregninger, og finn ut hvor langt tøystykke bedriften minst må bruke for å lage åtte gardiner.
Fasit
468.2 cm.
Løsning
Vi velger oss et koordinatssystem slik at \(x\)-aksen ligger midt på gardinen. Så velger vi \(x = 0\) til å samsvare med venstre side av gardinen. La \(f(x)\) være funksjonsuttrykket for den første parabelen øverst til venstre i tøystykket. Da vet vi at \(f(0) = 70\) og \(f(150) = 70.\) Siden funksjonsverdiene er de samme, må symmetrilinja ligge midt mellom de to punktene. Da kan vi bestemme symmetrilinja ved å ta gjennomsnittet av \(x\)-koordinatene:
Ekstremalpunktet til \(f\) ligger da på \(x\)-aksen i \((75, 0)\). Dermed kan vi skrive \(f(x)\) på ekstremalpunktsform som
Vi bestemmer \(a\) ved å bruke at \(f(0) = 70\):
Siden alle parablene er like, så vil denne verdien for \(a\) gjelde for alle parablene. Målet vårt er å bestemme hvor langt tøystykket minst må være. Fokuserer vi på den stiplede linja \(y = 35\), så kan vi observere at alle parablene skjærer hverandre ved denne linja. Hvis vi da kjenner til avstanden mellom disse skjæringspunktet, så har vi nesten avstanden til hele tøystykket. Vi mangler bare en bit på venstre side og en bit på høyre side som er like lange.
Vi starter med å finne avstanden mellom skjæringspunktene til \(f\) og linja \(y = 35\) siden dette vil gi oss begge avstandene vi trenger. Da løser vi likningen
Vi gjør dette med CAS:

Som betyr at
Her er \(x_2 > x_1\), så avstanden mellom de to punktene er
Videre vil \(x_1\) være avstanden fra starten av tøystykket til det første skjæringspunktene. Denne lengden opptrer én gang på hver side av tøystykket. Vi har 4 parabler, som betyr at lengden \(\Delta x\) opptrer 4 ganger. Dermed må lengden \(L\) av tøystykket minst være
Tøystykket bør altså være minst 468.2 cm langt for å lage åtte gardiner.