Vår 2025

Innhold

Vår 2025#

Generelt gis det ingen uttelling hvis bare riktig svar er oppgitt uten forklaringer, utregninger eller lignende. Husk at du alltid må

Forklare fremgangsmåte

Vise utregninger

Trekke en konklusjon der det er naturlig for å svare på oppgaven.

Del 1#

2 timer uten hjelpemidler

Oppgave 1

a

En andregradsfunksjon $f$ er gitt ved

\[ f(x) = x^2 - 3x - 4. \]

Bestem i hvilke punkter grafen til $f$ skjærer $x$-aksen.

Retteveiledning

Inntil 1 poeng for gyldig strategi.
Inntil 1 poeng for riktig svar.

Fasit

Grafen til $f$ skjærer $x$-aksen i $x = -1$ og $x = 4$.

Løsning

Grafen til $f$ skjærer $x$-aksen når $f(x) = 0$. Bruker $abc$-formelen til å finne røttene til $f(x)$:

\[ x = \dfrac{-(-3)\pm \sqrt{(-3)^2 - 4\cdot 1 \cdot (-4)}}{2\cdot 1} = \dfrac{3 \pm \sqrt{9 + 16}}{2} = \dfrac{3 \pm 5}{2}. \]

som gir

\[ x = 4 \or x = -1. \]

Dermed skjærer grafen til $f$ gjennom $x$-aksen i $x = -1$ og $x = 4$.

b

En andregradsfunksjon $g$ er gitt ved

\[ g(x) = -(x + 3)(x - 5). \]

Bestem ekstremalpunktet til $g$.

Retteveiledning

Inntil 1 poeng for gyldig strategi.
Inntil 1 poeng for riktig svar.

Det gis full uttelling om bare $x$-koordinaten er oppgitt, men det gis også full uttelling om en $y$-koordinat er oppgitt i tillegg, selv hvis feil $y$-koordinat er oppgitt.
Det er forvirring rundt definisjonen av ekstremalpunkt (trolig på grunn av Geogebra), men det er formelt sett bare $x$-koordinaten til et bunn- eller toppunkt.

Fasit

\[ x = 1. \]

Løsning

Ekstremalpunktet $x_0$ til $g$ svarer til symmetrilinja til grafen som vi kan finne ved å ta gjennomsnittet av nullpunktene. Vi har at

\[ g(x) = 0 \liff (x + 3)(x - 5) = 0 \liff x = -3 \or x = 5. \]

som betyr at

\[ x_0 = \dfrac{(-3) + 5}{2} = \dfrac{2}{2} = 1. \]

Dermed er ekstremalpunktet til $g$ i $x = 1$.

c

En andregradsfunksjon $h$ er gitt ved

\[ h(x) = -(x + 2)^2 + 5 \quad \text{der} \quad D_h = \mathbb{R}. \]

Bestem verdimengden til $h$.

Retteveiledning

Inntil 1 poeng for gyldig strategi.
Inntil 1 poeng for riktig svar.

Fasit

\[ h(x) \in \langle \gets, 5]. \]

Løsning

Verdimengden til $h$ vil være alle verdier $h(x)$ vi kan få fra $x \in D_h = \mathbb{R}$. Siden definisjonsmengden er alle reelle tall, må vi avgjøre hvilke verdier $h(x)$ kan ta helt generelt. Siden $h$ er en andregradsfunksjon, følger det at den enten har et topp- eller bunnpunkt. Siden den ledende koeffisienten til $h$ er negativ, har den et toppunkt. Videre er $h(x)$ skrevet på ekstremalform

\[ h(x) = -(x + 2)^2 + 5, \]

som betyr at vi kan lese av toppunktet som $(-2, 5)$. Dermed er $h(x) \leq 5$ for alle $x \in D_h$. Verdimengden til $h$ er derfor

\[ h(x) \in \langle \gets, 5]. \]

Oppgave 2

Nedenfor vises en trekant $\triangle ABC$.

Retteveiledning

Inntil 1 poeng for å bestemme $AC$ med en gyldig strategi.
Inntil 1 poeng for å bestemme $\tan 60 \degree$ med en gyldig strategi.

Fasit

\[ \tan 60 \degree = \sqrt{3} \]

Løsning

I figuren har vi at

\[ \tan 60 \degree = \dfrac{AB}{AC} = \dfrac{2\sqrt{3}}{AC} \]

siden $AB$ er motstående katet og $AC$ er hosliggende katet til $\angle C$. Vi kan bruke Pytagoras’ setning til å bestemme $AC$:

\[ AC^2 + (2\sqrt{3})^2 = 4^2 \liff AC^2 + 12 = 16 \liff AC^2 = 4 \]

dermed er

\[ AC = 2. \]

Da følger det at

\[ \tan 60 \degree = \dfrac{2\sqrt{3}}{AB} = \dfrac{2\sqrt{3}}{2} = \sqrt{3}. \]

Oppgave 3

Grafen til en andregradsfunksjon $f$ er vist i figuren nedenfor.

a

Bestem $f(x)$.

Retteveiledning

Inntil 1 poeng for å velge en gyldig fremgangsmåte.
1 poeng for å bestemme riktig $f(x)$.

Fasit

\[ f(x) = -(x + 2)(x - 4) = -x^2 + 2x + 8. \]

Løsning

Grafen til $f$ skjærer $x$-aksen i $x = - 2$ og $x = 4$ som betyr at vi kan skrive $f(x)$ på nullpunktsform:

\[ f(x) = a(x + 2)(x - 4). \]

Grafen til $f$ skjærer $y$-aksen i $y = 8$ som betyr at

\[ f(0) = 8 \liff a(0 + 2)(0 - 4) = 8 \liff -8a = 8 \liff a = -1. \]

Dermed følger det at

\[ f(x) = -(x + 2)(x - 4) = -x^2 + 2x + 8. \]

b

Bestem likningen til tangenten i $(3, f(3))$.

Retteveiledning

Inntil 1 poeng for å velge en gyldig fremgangsmåte.
1 poeng for riktig likning for tangenten.

Fasit

\[ y = -4x + 17. \]

Løsning

Strategi 1: Den deriverte

For å bestemme likningen til tangenten i $(3, f(3))$ må vi finne $y$-koordinaten til punktet og stigningstallet til tangenten.

\[ y_1 = f(3) = -(3 + 2)(3 - 4) = 5. \]

Stigningstallet $a$ til tangenten er gitt ved den deriverte i $x = 3$:

\[\begin{align*} f'(x) &= -2x + 2 \\ \\ a = f'(3) &= -2(3) + 2 = -6 + 2 = -4. \end{align*}\]

Vi bruker ettpunktsformelen til å bestemme likningen

\[\begin{align*} y - y_1 &= a(x - x_1) \\ \\ y - 5 &= -4(x - 3) \\ \\ y - 5 &= -4x + 12 \\ \\ y &= -4x + 17. \end{align*}\]

Altså er likningen til tangenten

\[ y = -4x + 17. \]

Strategi 2: Polynomdivisjon

Resten i polynomdivisjonen $f(x) : (x - 3)^2$ gir oss uttrykket for tangenten i $x = 3$.

Fra resten i polynomdivisjonen finner vi at likningen er

\[ y = -4x + 17. \]

Oppgave 4

En rasjonal funksjon $f$ er gitt ved

\[ f(x) = \dfrac{x^2 - 1}{x^2 - 2x + 1} \]

Avgjør hvilken graf som tilhører $f$.

Husk å forklare hvordan du kommer fram til svaret ditt.

Retteveiledning

Inntil 2 poeng for å bestemme relevante egenskaper for $f$.
Inntil 1 poeng for å bestemme riktig graf ut ifra egenskapene.

Fasit

Graf B.

Løsning

Vi nullpunktsfaktoriserer teller- og nevnerpolynomet i $f(x)$:

\[ f(x) = \dfrac{x^2 - 1}{x^2 - 2x + 1} = \dfrac{(x + 1)(x - 1)}{(x - 1)^2} = \dfrac{x + 1}{x - 1} \]

der vi brukte konjugatsetningen i tellerpolynomet og 2.kvadratsetning i nevnerpolynomet. Ettersom vi nå har forkortet bort alle felles faktorer, kan vi bestemme $f$ sine nullpunkter og asymptoter.

Fra tellerpolynomet i det fortkortede uttrykket får vi at

\[ f(x) = 0 \liff x + 1 = 0 \liff x = -1 \]

som betyr at $f$ har et nullpunkt i $x = -1$. Fra nevnerpolynomet får vi at

\[ x - 1 = 0 \liff x = 1 \]

som betyr at $f$ har en vertikal asymptote i $x = 1$. Siden ledende koeffisient for teller og nevnerpolynomet er $1$ og polynomeme er av samme grad, følger det at den horisontale asymptoten er $y = 1$.

Graf $B$ er den eneste grafen som samtidig har

et nullpunkt for $x < 0$
en vertikal asymptote når $x > 0$
en horisontal asymptote der $y > 0$.

Dermed må graf B gære grafen til $f$.

Oppgave 5

I figuren nedenfor til venstre vises en sirkel med radius $1$ og en trekant som har to hjørner på sirkelen.

I figuren nedenfor til høyre vises en trekant $\triangle ABC$.

Bestem arealet av $\triangle ABC$.

Retteveiledning

Inntil 1 poeng for å sette opp riktig formel for arealet med arealsetningen.
Inntil 1 poeng for å bestemme $\sin 120 \degree$ med en gyldig strategi.
Bruk av formlikhet for å bestemme arealet kan også gi full uttelling.

Fasit

Arealet er $4\sqrt{3}$.

Løsning

Først kan vi merke oss at $\triangle ABC$ er likebeint siden $\angle A = 120\degree$ og $\angle B = 30 \degree$ som betyr at

\[ \angle C = 180 \degree - 30\degree - 120 \degree = 30 \degree. \]

Dermed følger det at $AB = AC = 4$. Vi kan derfor bruke arealsetningen med utgangspunkt i hjørne $A$:

\[ T_{\triangle ABC} = \dfrac{1}{2}\cdot AB \cdot AC \cdot \sin \angle A = \dfrac{1}{2} \cdot 4 \cdot 4 \cdot \sin 120\degree = 8 \cdot \sin 120 \degree. \]

Fra figuren med enhetssirkelen, har vi fått oppgitt et punkt på enhetssirkelen som svarer til en vinkel på $120 \degree$. Da vil $y$-koordinaten til dette punktet være $\sin 120\degree$. Dermed har vi at

\[ \sin 120 \degree = \dfrac{\sqrt{3}}{2}. \]

Da følger det at arealet av $\triangle ABC$ er

\[ T_{\triangle ABC} = 8 \cdot \dfrac{\sqrt{3}}{2} = 4\sqrt{3}. \]

Oppgave 6

En elev jobber med en funksjon $f$. Grafen til $f$ er vist i figuren nedenfor.

Eleven har skrevet programmet nedenfor

def f(x):
    return x**3 + x**2 - 5 * x + 3


for x in range(0, 6):
    print(f(x))

som ga utskriften

a

Bestem én mulighet for verdiene til $a$, $b$ og $c$ slik at likningen nedenfor er en identitet.

\[ x^3 + x^2 - 5x + 3 = (x - a)(x - b)(x - c). \]

Retteveiledning

Inntil 1 poeng for å velge en gyldig fremgangsmåte.
1 poeng for å bestemme én mulighet for $a$, $b$ og $c$.

Fasit

\[ a = -3 \and b = c = 1 \]

Løsning

Programmet til eleven bruker en for-løkke som går gjennom verdiene $x \in \{0, 1, 2, \ldots, 5\}$. Fra utskriften kan vi se at den 2. verdien som skrives ut er $0$ som betyr at $f(1) = 0$. Dermed er $x = 1$ et nullpunkt.

Fra figuren kan vi se at det positive nullpunktet til $f$ også er et bunnpunkt som betyr at det er et dobbelt nullpunkt. Da vet vi at $(x - 1)^2 | f(x)$ og polynomdivisjonen $f(x) : (x - 1)^2$ vil gå opp:

Fra polynomdivisjonen følger det at

\[ (x^3 + x^2 - 5x + 3) = (x + 3)(x - 1)^2 \]

som betyr at én mulighet for verdiene til $a$, $b$ og $c$ er

\[ a = -3 \and b = c = 1. \]

b

Løs ulikheten $f(x) < 0$.

Retteveiledning

Inntil 1 poeng for å velge en gyldig fremgangsmåte.
Inntil 1 poeng for riktig svar.

Fasit

\[ x \in \langle \gets, -3 \rangle. \]

Løsning

Fra grafen til $f$, kan vi se at $f(x) < 0$ når for alle verdier av $x$ som ligger på nedsiden av det negative nullpunktet til $f$. Det negative nullpunktet til $f$ er $x = -3$.

Dermed kan vi konkludere at

\[ f(x) < 0 \liff x \in \langle \gets, -3 \rangle. \]

Del 2#

3 timer med hjelpemidler

Oppgave 1

På bakkenivå er lufttrykket 1 atm (atmosfærisk trykk). Lufttrykket avtar med $12 \, \%$ per km i høyden.

a

Forklar at en modell som passer med beskrivelsen ovenfor er

\[ L(x) = 1 \cdot 0.88^x \]

der $L(x)$ er det atmosfæriske trykket $x$ kilometer over bakken.

Retteveiledning

Inntil 1 poeng for å forklare at $L$ er en eksponentiell modell $L(x) = a \cdot b^x$.
Inntil 1 poeng for å forklare verdiene $a$ og $b$ ut ifra opplysningene i oppgaven.

Løsning

$L$ vil være en eksponentiell modell siden lufftrykket avtar med en prosentvis endring per km. Derfor er det modell på formen

\[ L(x) = a \cdot b^x \]

der $a$ er startverdien ved $x = 0$ og $b$ er vekstfaktoren. Ved $x = 1$ er $L(0) = 1$ som betyr at $a = 1$. Siden lufttrykket avtar med $12 \, \%$ per km, er vekstfaktoren $b = 1 - 0.12 = 0.88$. Dermed får vi at

\[ L(x) = a \cdot b^x = 1 \cdot 0.88^x \]

b

Ved hvilken høyde er lufttrykket halvparten av det på bakkenivå?

Retteveiledning

Inntil 1 poeng for å forklare å velge en gyldig fremgangsmåte.
Inntil 1 poeng for riktig svar.

Fasit

Ca. $5.42$ km over bakken.

Løsning

For å bestemme hvilken høyde lufttrykket er halvparten av det på bakkenivå, må vi løse likningen

\[ L(x) = \frac{1}{2}L(0) \]

Vi bruker CAS til å løse likningen:

som betyr at lufttrykket er halvparten av det på bakkenivå ved $x \approx 5.42$ km over bakken.

c

Bestem stigningstallet til linja som går gjennom $(0, L(0))$ og $(8, L(8))$.
Gi en praktisk tolkning av svaret.

Retteveiledning

1 poeng for å bestemme riktig stigningstall.
1 poeng for riktig praktisk tolkning av svaret.

Løsning

Stigningstallet til linja som går gjennom punktene $(0, L(0))$ og $(8, L(8))$ svarer til den gjennomsnittlige vekstfarten til $L$ i intervallet $[0, 8]$. Vi regner ut dette med CAS:

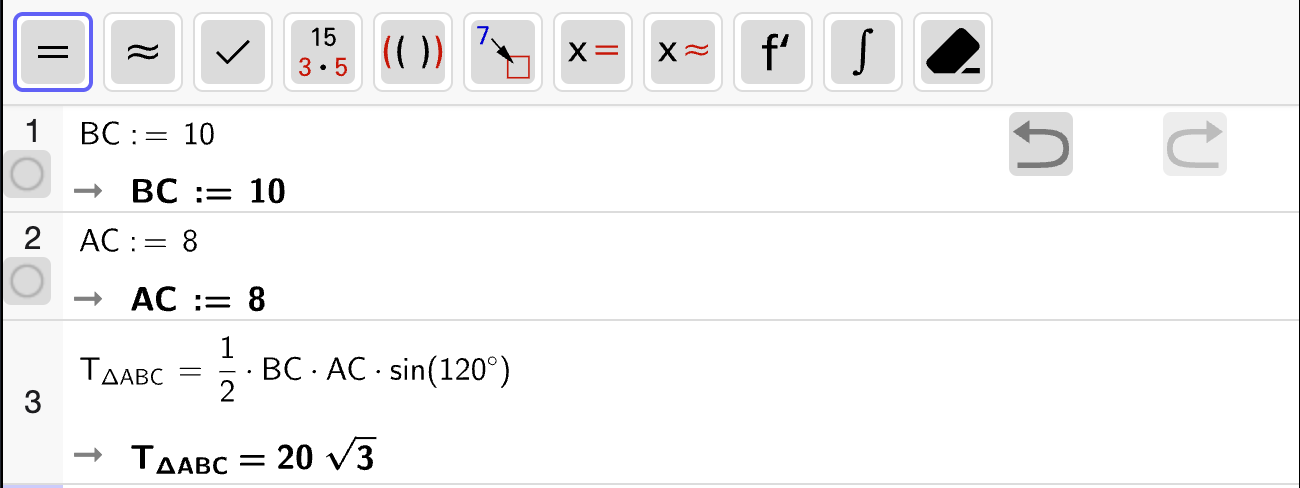
Stigningstallet til linja er altså ca. $-0.08$ atm/km. Det betyr at lufttrykket i gjennomsnitt blir $0.08$ atm lavere per km i høyden fra bakkenivå opp til $8$ km over bakken.

Oppgave 2

En regulær 6-kant er en 6-kant der alle sidene er like lange.

En sirkel med radius $1$ er innskrevet i en regulær 6-kant. En trekant har et hjørne i sentrum av sirkelen. Se figuren nedenfor.

Bruk trigonometri til å bestemme arealet av 6-kanten.

Retteveiledning

Inntil 1 poeng for å bestemme sidelengdene i trekanten med en gyldig strategi.
Inntil 1 poeng for å bestemme arealet av trekanten.
Inntil 1 poeng for å bestemme arealet av 6-kanten.

Fasit

Arealet av 6-kanten er $2\sqrt{3}$.

Løsning

6-kanten består av 6 like store trekanter. Vi trenger derfor å bestemme arealet av én slik trekant først. La trekanten som er tegnet inn være $\triangle ABC$ der $A$ er hjørnet i sentrum av sirkelen. Vi kan først merke oss at sentralvinkelen $\angle A = u$ vil være

\[ \angle A = \frac{360\degree}{6} = 60\degree. \]

siden det er $360\degree$ i en hel sirkel og det er 6 like store toppvinkler i de 6 trekantene vi har plass til med toppunkt i sentrum av sirkelen.

Trekant $\triangle ABC$ er minimum en likebeint trekant siden $AB = AC$. Videre er $\angle A = 60\degree$ som betyr at $\angle B = \angle C = 60\degree$ og trekanten er derfor også likesidet. Vi kan derfor lage følgende hjelpefigur der vi trekker en midtnormal fra hjørne $A$ ned på $BC$ som deler $\angle A$ nøyaktig i to like store vinkler, og tilsvarende deler $BC$ i to like lange linjestykker. Siden radien i sirkelen er $1$, følger det at lengden på midtnormalen er $1$. Vi lar sidelengdene i trekanten være $\ell$. Se figuren nedenfor.

I utregningen nedenfor bruker vi at $\sin 60 \degree = \cos 30 \degree = \dfrac{\sqrt{3}}{2}$.

Fra definisjonen av cosinus, kan vi da skrive

\[ \cos 30 \degree = \dfrac{1}{\ell} \liff \ell = \dfrac{1}{\cos 30 \degree} = \dfrac{1}{\sqrt{3}/2} = \dfrac{2}{\sqrt{3}}. \]

Deretter bruker vi arealsetningen for å bestemme arealet av trekant $\triangle ABC$:

\[ T_{\triangle ABC} = \dfrac{1}{2} \cdot \ell^2 \cdot \sin 60\degree = \dfrac{1}{2} \cdot \left(\dfrac{2}{\sqrt{3}}\right)^2 \cdot \dfrac{\sqrt{3}}{2} = \dfrac{1}{2} \cdot \dfrac{4}{3} \cdot \dfrac{\sqrt{3}}{2} = \dfrac{\sqrt{3}}{3}. \]

6-kanten består av 6 slike trekanter, så det samlede arealet blir da

\[ T_{6-\mathrm{kant}} = 6 \cdot T_{\triangle ABC} = 6 \cdot \dfrac{\sqrt{3}}{3} = 2\sqrt{3}. \]

Oppgave 3

Nedenfor vises grafen til en andregradsfunksjon $f$ og to tangenter som skjærer gjennom nullpunktene til $f$.

Den ene tangenten har stigningstall $4$.
Tangentene skjærer hverandre i $(-1, -8)$.

Retteveiledning

Inntil 1 poeng for å sette opp et gyldig likningssystem for koeffisientene til $f(x)$ eller $f'(x)$.
1 poeng for å bestemme $f(x)$ med en gyldig fremgangsmåte.
1 poeng for å bestemme $f'(x)$ med en gyldig fremgangsmåte.

Andre gyldige fremgangsmåter som leder fram til $f(x)$ og $f'(x)$ vil også gi full uttelling.

Fasit

\[ f(x) = x^2 + 2x - 3 \limplies f'(x) = 2x + 2. \]

Løsning

Vi kan sette opp et likningssystem ut ifra opplysningene i oppgaven. Vi trenger tre likninger der minst én av de ikke er en nullpunktslikning.

Begge tangenter går gjennom punktet $(-1, -8)$. Den ene tangenten har stigningstall $4$. Fra ettpunktsformelen kan vi dermed skrive ned likningen til denne tangenten som:

\[ y - (-8) = 4(x - (-1)) \liff y = 4x - 4 = 4(x - 1) \]

Her kan vi konkludere at tangenten skjærer $x$-aksen i

\[ y = 0 \liff 4(x - 1) = 0 \liff x = 1 \]

Det betyr at vi fra denne tangenten kan sette opp likningene

\[\begin{align*} f(1) &= 0 && \text{Nullpunkt i $x = 1$} \\ \\ f'(1) &= 4 && \text{Stigningstallet til tangenten i $x = 1$} \\ \end{align*}\]

Den andre tangenten går gjennom det andre nullpunktet til $f$. På grunn av symmetrien til en andregradsfunksjon, betyr det at $x$-koordinaten til skjæringspunktet mellom de to tangentene svarer til symmetrilinja til $f$. Dermed vil en tangent i punktet ha stigningstall $0$ slik at den siste likningen vi trenger er

\[\begin{align*} f'(-1) &= 0 && \text{Stigningstallet til tangenten i $x = -1$. Bunnpunkt} \\ \end{align*}\]

En andregradsfunksjon $f$ er generelt sett gitt ved

\[ f(x) = ax^2 + bx + c. \]

Vi løser likningssystemet med CAS for å bestemme koeffisientene til $f(x)$:

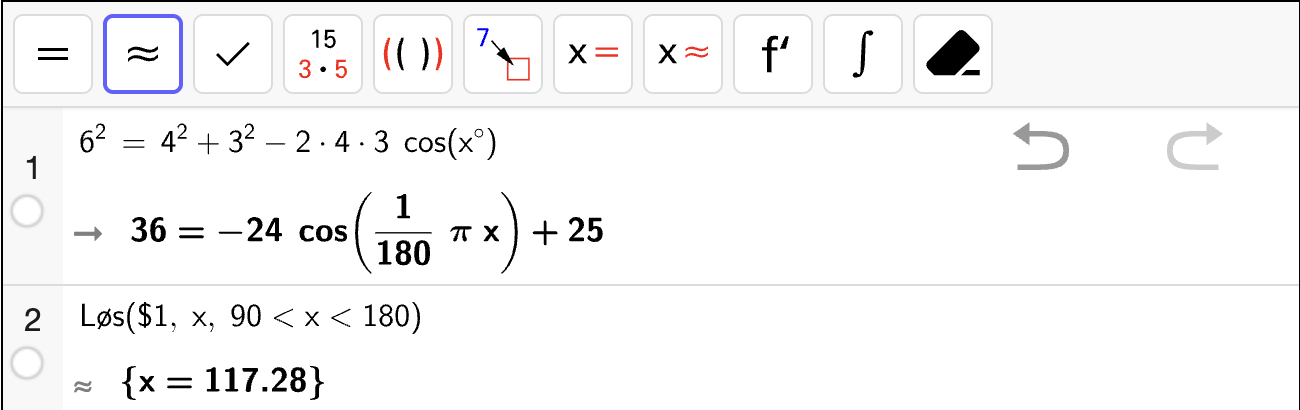
som betyr at

\[ f(x) = x^2 + 2x - 3. \]

Deriverer vi uttrykket, får vi:

\[ f'(x) = (x^2 + 2x - 3)' = 2x + 2. \]

Andre likninger vi kunne hentet ut fra opplysningene i oppgaven er:

$f(-3) = 0$

$f'(-3) = -4$

Oppgave 4

Nedenfor vises en sylinder fylt med vann med et lite hull i bunnen.

Den horisontale avstanden vannstrålen beveger seg er $S_i$ meter når vannstanden er $x_i$ meter over bunnen av sylinderen. I tabellen nedenfor vises et datamateriale for dette.

$x$ (meter)	$8$	$6$	$5$	$3$	$2$
$S$ (meter)	$5.66$	$4.90$	$4.47$	$3.46$	$2.83$

a

Lag en modell på formen

\[ S(x) = a \cdot x^b \]

som viser hvor mange meter $S(x)$ vannstrålen beveger seg horisontalt når vannstanden er $x$ meter over bunnen av sylinderen.

Retteveiledning

Inntil 1 poeng for å velge en gyldig fremgangsmåte.
1 poeng for å bestemme en rimelig modell $S(x)$.

Fasit

\[ S(x) \approx 2 \cdot x^{0.5} = 2\sqrt{x} \]

Løsning

Vi skriver inn datapunktene i et regneark i Geogebra:

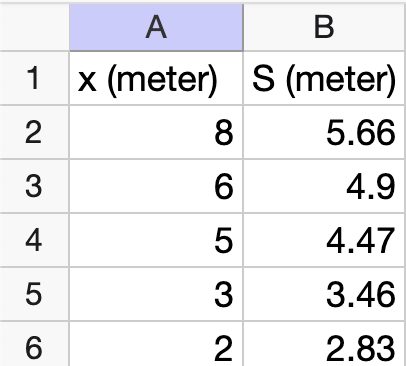
Deretter gjør vi regresjonsanalyse og velger en potensfunksjon som modell siden dette er modelltypen som er oppgitt som gir:

som betyr at

\[ S(x) \approx 2\cdot x^{0.5} = 2\sqrt{x} \]

er en passende modell for datamaterialet.

Vi definerer $S(x)$ som dette i resten av oppgaven.

b

Etter at hullet ble åpnet, varierte høyden til vannstanden med tiden slik at den kan beskrives av en modell på formen

\[ h(t) = k(t - r)^2. \]

Når hullet i bunnen ble åpnet var vannstanden $10$ meter over bunnen. Tanken ble halvfull etter $7$ sekunder.

Bestem $k$ og $r$. Gi en praktisk tolkning av konstanten $r$.

Retteveiledning

Inntil 1 poeng for å bestemme $k$ og $r$.
Inntil 1 poeng for å gi en praktisk tolkning av konstanten $r$.

Fasit

\[ k \approx 0.02 \and r \approx 23.9 \]

Den praktiske tolkningen av $r$ er at det tar $r \approx 23.9$ sekunder før tanken er tom for vann.

Løsning

Modellen $h$ er en andregradsfunksjon skrevet på ekstremalform. Fra opplysningene kan vi sette opp et likningssystem:

\[\begin{align*} h(0) &= 10 && \text{(høyden når hullet åpnes er 10 meter)} \\ \\ h(7) &= 5 && \text{(tanken er halvfull etter 7 sekunder)} \\ \end{align*}\]

Vi bestemmer $k$ og $r$ ved å løse likningssystemet i CAS:

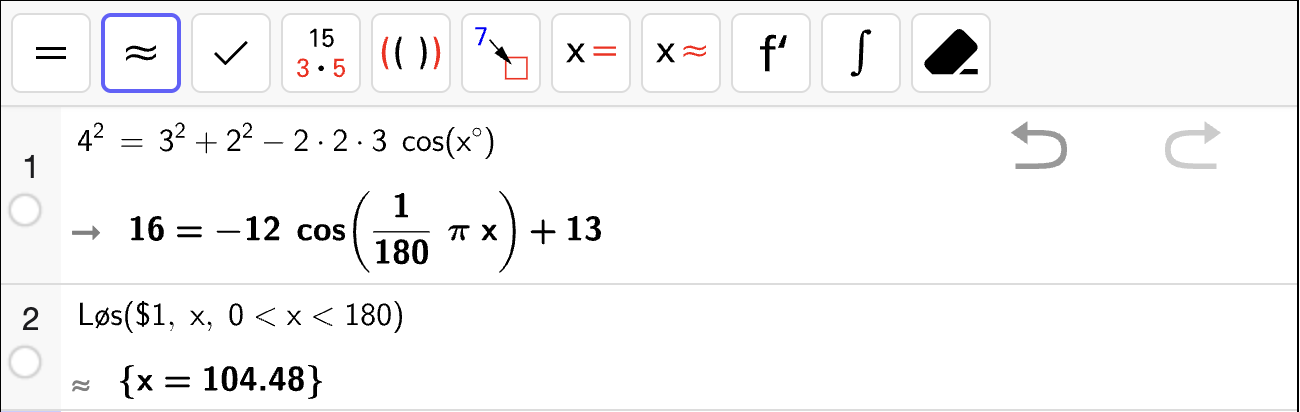
som gir oss at

\[ k \approx 0.02 \and r \approx 23.9 \]

Siden $h(t)$ er skrevet på ekstremalform med en ekstremalverdi som er $y_0 = 0$, vil $t = r$ svare til $t$-koordinaten til bunnpunktet og nullpunktet til $h$. Den praktiske tolkningen er at det tar $r = 23.9$ sekunder før tanken er tom for vann.

c

Hvor lang tid tar det før lengden av strålen og høyden på vannstanden er like?

Retteveiledning

Inntil 1 poeng få bestemme ved hvilken høyde strålen og høyden på vannstanden er like.
Inntil 1 poeng for å bestemme hvor lang tid det tar før strålen og høyden på vannstanden er like.

Andre gydlige fremgangsmåter for å bestemme hvor lang tid det tar før strålen og høyden på vannstanden er like vil også gi full uttelling.

Fasit

$t \approx 9.76$ sekunder

Løsning

Vi har to modeller:

$S(x)$ som gir oss lengden av strålen for en gitt høyde $x$ på vannstanden.
$h(t)$ som gir oss høyden på vannet for en gitt tid $t$.

For å bestemme hvor lang tid det tar før lengden av strålen og høyden på vannstanden er like, løser vi oppgaven i to steg:

Vi løser $S(x) = x$ for å avgjøre når strålen og høyden er like.
Vi løser $h(t) = x$ for løsningen vi fikk i steg 1 for å avgjøre når vi er ved høyden som er lik lengden av strålen.

Vi løser dette med CAS:

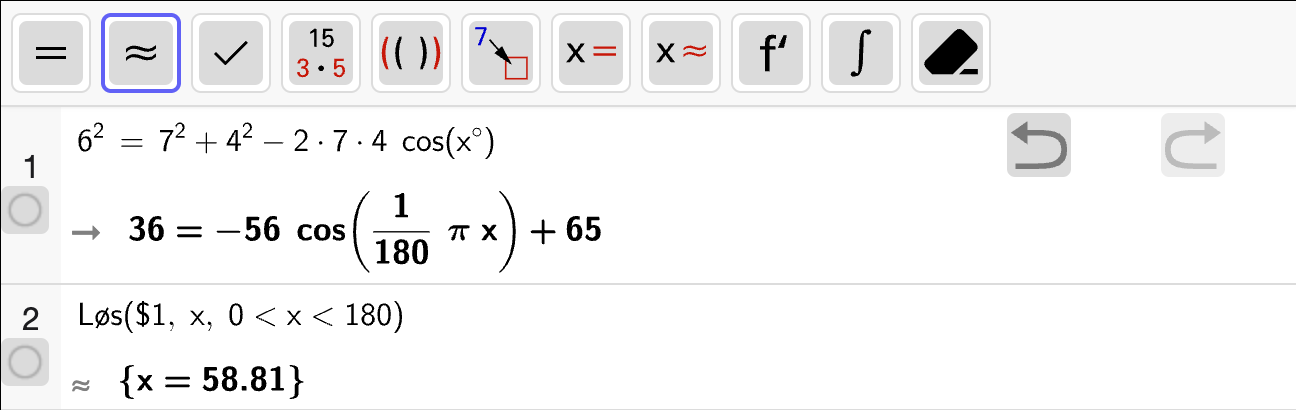
Her finner vi fra steg 1 at $x = 4$ er høyden der lengden av strålen og høyden på vannstanden er like. Så løser vi $h(t) = 4$ for å avgjøre hvor lang tid det tok før vannstanden hadde denne høyden, som ga oss to løsninger:

\[ t \approx 9.76 \or t \approx 38.04. \]

Men vi vet allerede at vanntanken er tom etter $t \approx 23.9$ sekunder, som betyr at vi kan konkludere at høyden til vannstanden og lengden på vannstrålen var like etter $t \approx 9.76$ sekunder.

Oppgave 5

En båt skal reise fra en øy $A$ til en øy $C$.
Båten må innom land på en kystlinje på et punkt $B$ for å hente ferskvann. Båten skal reise en så kort som mulig avstand for å spare drivstoff.

Kystlinjen er $9$ km lang. Øy $A$ ligger $2$ km fra land og øy $C$ ligger $4$ km fra land. Se figuren nedenfor.

En strandkiosk $S$ er plassert på starten av kystlinja.

a

Bestem lengden båten må kjøre fra $A$ til $C$ dersom den går i land $2$ km fra strandkiosken.

Retteveiledning

Inntil 1 poeng for å bruke Pytagoras’ setning til å bestemme lengdene $AB$ og $BC$.
Inntil 1 poeng for å bestemme den totale lengden på reisen fra $A$ til $C$.

Fasit

Ca. $10.89$ km

Løsning

Vi bruker Pytagoras’ setning på de to trekantene med $x = 2$ km som gir at de horisontale katetene er henholdsvis $2$ km og $(9 - 2)$ km. Vi regner ut summen av lengdene $AB + BC$ med CAS:

som betyr at båten da kjører ca. $10.89$ km.

b

Lag en modell $L$ som gir lengden $L(x)$ som båten må kjøre dersom den går i land en avstand $x$ fra strandkiosken.

Retteveiledning

Inntil 1 poeng for å bruke Pytagoras’ setning til å bestemme lengdene $AB$ og $BC$.
Inntil 1 poeng for å sette opp modellen $L(x)$.

Fasit

\[ L(x) = \sqrt{4 + x^2} + \sqrt{16 + (9 - x)^2} \]

Løsning

Lengden $L(x)$ vil være summen av lengdene $AB$ og $BC$ for en bestemt verdi av $x \in [0, 9]$. Med Pytagoras’ setning følger det at:

\[\begin{align*} AB^2 &= 2^2 + x^2 \limplies AB = \sqrt{4 + x^2} \\ \\ BC^2 &= 4^2 + (9 - x)^2 \limplies BC = \sqrt{16 + (9 - x)^2} \\ \end{align*}\]

Dermed er modellen $L$ gitt ved

\[ L(x) = AB + BC = \sqrt{4 + x^2} + \sqrt{16 + (9 - x)^2} \]

c

Bestem hvor langt unna strandkiosken båten må gå i land for å få kortest mulig reisevei fra $A$ til $C$.

Retteveiledning

Inntil 1 poeng for å velge riktig fremgangsmåte.
Inntil 1 poeng for å bestemme $x$ slik at reiseveien er kortest mulig. Maksimalt 0,5 poeng hvis det ikke argumentert for at $x$ gir et bunnpunkt.

Fasit

\[ x = 3 \]

Løsning

For å bestemme hvor langt unna strandkiosken båten må gå i land for å få kortest mulig reisevei, løser vi likningen $L'(x) = 0$ for å finne kandidater for bunnpunkter til $L$. Vi løser likningen med CAS:

som forteller oss at $x = 3$ er en kandidat for et bunnpunkt. For å være sikre på at dette er et bunnpunkt, holder det å sjekke $L(x)$ i endepunktene og sammenligne med $L(3)$:

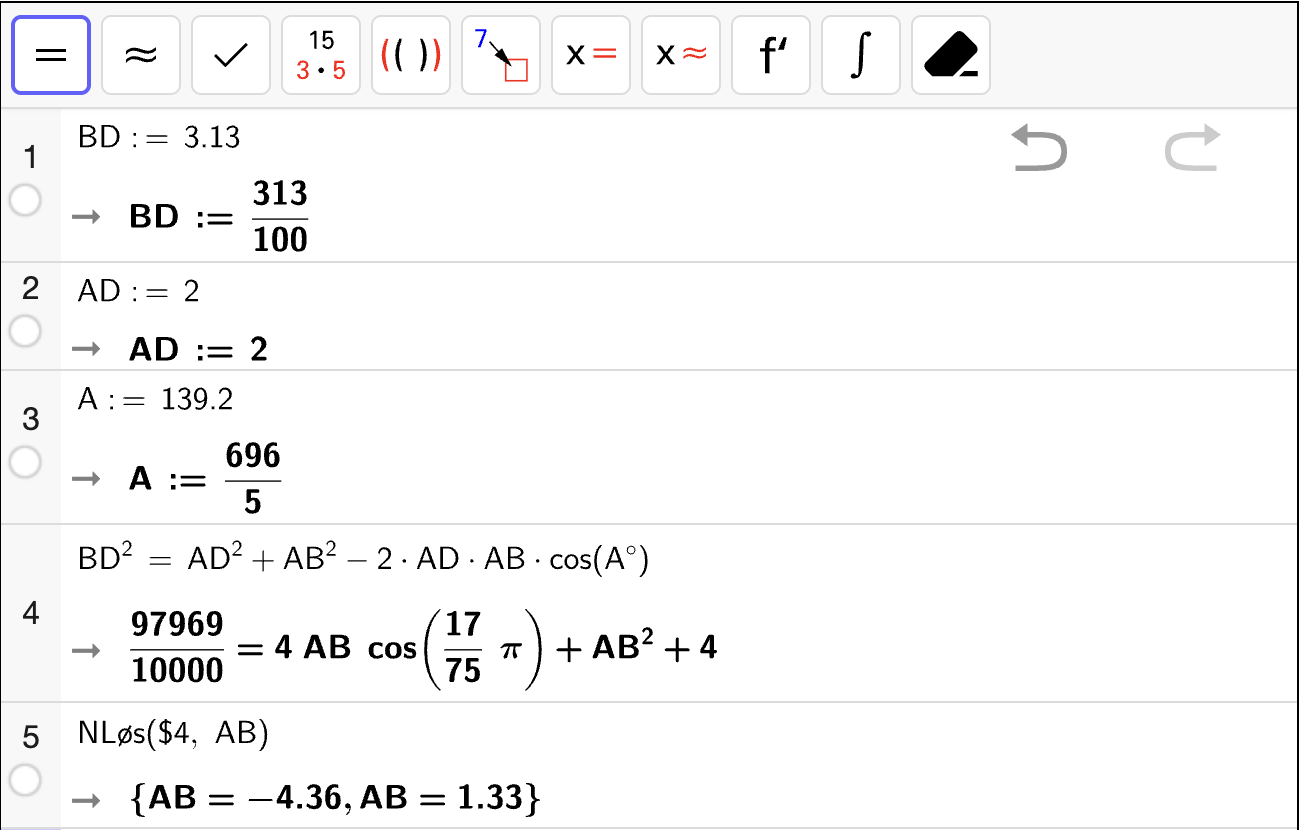
Vi ser altså at $L(3) < L(0)$ og $L(3) < L(9)$, og dermed er $x = 3$ et bunnpunkt. Dermed må båten gå i land $3$ km fra strandkiosken for å få kortest mulig reisevei fra $A$ til $C$.

Oppgave 6

Nedenfor vises et kvadrat med sidelengder $3$.

Kvadratet er fylt med mindre fargelagte kvadrater som blir mindre og mindre.

Lag et program som regner ut summen av arealet til de 100 største fargelagte kvadratene.

Retteveiledning

Inntil 1 poeng for å skrive et program som bruker en løkke som regner ut arealet av $100$ kvadrater.
Inntil 1 poeng for å bestemme riktig sum av arealene.

Mindre mangler i programmet kan fortsatt gi noe uttelling. Programmet bør være rimelig forklart med kommentarer eller en overordnet forklaring for å gi full uttelling.

Løsning

Først kan vi legge merke til at sidelengdene i det største fargelagte kvadratet er $3/2$. Deretter halveres sidelengden for hvert mindre fargelagte kvadrat. For å summere arealet til de 100 største fargelagte kvadratene, kan vi derfor bruke en løkke som gjør følgende:

Regner ut arealet $A$ av kvadratet med sidelengde $\ell$ ved $A = \ell^2$.
Legger til arealet til summen $s \to s + A$.
Halverer sidelengden $\ell \to \ell / 2$.

Vi gjentar dette 100 ganger.

Programkode:

s = 0 # sum av arealer
lengde = 3 / 2 # sidelengder i første kvadrat

# summerer de 100 største fargelagte kvadratene
for i in range(100):
    areal = lengde ** 2 # areal av kvadrat
    s = s + areal    # legg til arealet
    
    lengde = lengde / 2 # halver sidelengden

print(s)

Utskrift:

2.9999999999999996

Arealet til de 100 største fargelagte kvadratene er ca. $3$.

Oppgave 7

Nedenfor vises noen påstander.

Avgjør om påstandenen er sanne eller usanne.
Husk å forklare hvordan du kommer fram til svarene dine.

Påstand 1: Hvis $f$ er en polynomfunksjon og $f(-1) = f(3)$, så er $f'(1) = 0$.

Påstand 2: Hvis $f(x)$ er et polynom av grad $5$, så må $f(x) = 0$ for minst én verdi av $x$.

Påstand 3: Funksjon $f$ gitt ved

\[ f(x) = \dfrac{(x - 3)^m}{x^2 - 6x + 9} \quad \text{der} \quad m \in \mathbb{N} \]; har en vertikal asymptote kun når $m = 1$.

Retteveiledning

Inntil 1 poeng for hver påstand som er vurdert riktig.

Riktig svar uten argumentasjon gir ingen uttelling.

Løsning

Påstand 1

Påstanden er usann. Påstanden er bare sann for andregradsfunksjoner, men generelt så vil det bare finnes et tall $c \in \langle -1, 3\rangle$ hvor $f'(c) = 0$, men dette punktet må ikke nødvendigvis være midt i intervallet.

Vi kan vise dette med et moteksempel ved å se på en tredjegradsfunksjon der $f(-1) = f(3)$. Én slik tredjegradsfunksjon er:

\[ f(x) = (x + 1)(x - 3)^2 \]

siden her er $f(-1) = f(3) = 0$. Så kan vi bestemme i hvilke punkter $x$ vi får $f'(x) = 0$ og undersøke hvor i intervallet $[-1, 3]$ et av disse punktene ligger.

Her finner vi at $x = \dfrac{1}{3}$ er det eneste punktet som ligger i intervallet $\langle -1, 3 \rangle$. Men dette punktet er ikke $x = 1$ (midt i intervallet), så vi har motbevist påstanden.

Påstand 2

Påstanden er sann fordi alle oddegradspolynomer må minst ha ett nullpunkt fordi et polynom $f(x)$ alltid kan faktoriseres i et produkt av lineære faktorer og andregradsfaktorer. For at vi skal få en oddetallspotens som høyeste potens må det alltid være minst én lineær faktor $(x - r)$ i $f(x)$ som sikrer at $f(x) = 0$ for minst én verdi av $x = r$.

Påstand 3

Påstanden er sann som vi kan se ved å faktorisere nevneren:

\[ f(x) = \dfrac{(x - 3)^m}{(x - 3)^2} \]

Bare når $m = 1$ vil vi ha færre faktorer av $(x - 3)$ i telleren enn i nevneren som dermed gir en vertikal asymptote i $x = 3$. For alle andre naturlig tall $m$ vil vi enten ha like mange faktorer eller flere i telleren som bare gir et bruddpunkt i $x = 3$.