Oppgaver: Modellering

Tips: Oppgave 1

I oppgaver hvor du skal vise at modell er en god modell, så er det ofte lurt å bare utføre regresjon med datamateriale du har fått og velge den samme modelltypen som er oppgitt.

---

For å lage en polynomfunksjon som en regresjonsmodell, kan du bruke RegPoly(data, polynomgrad).

Oppgave 1

Åpne CAS‑vindu

Tabellen nedenfor viser hvor mange bagetter en kantine har solgt hver av de siste sju ukene, og hvor stort overskudd salget har gitt.

Solgte bagetter	100	130	160	175	190	220	235
Overskudd (kroner)	1450	2300	3050	3365	3720	4140	4175

a

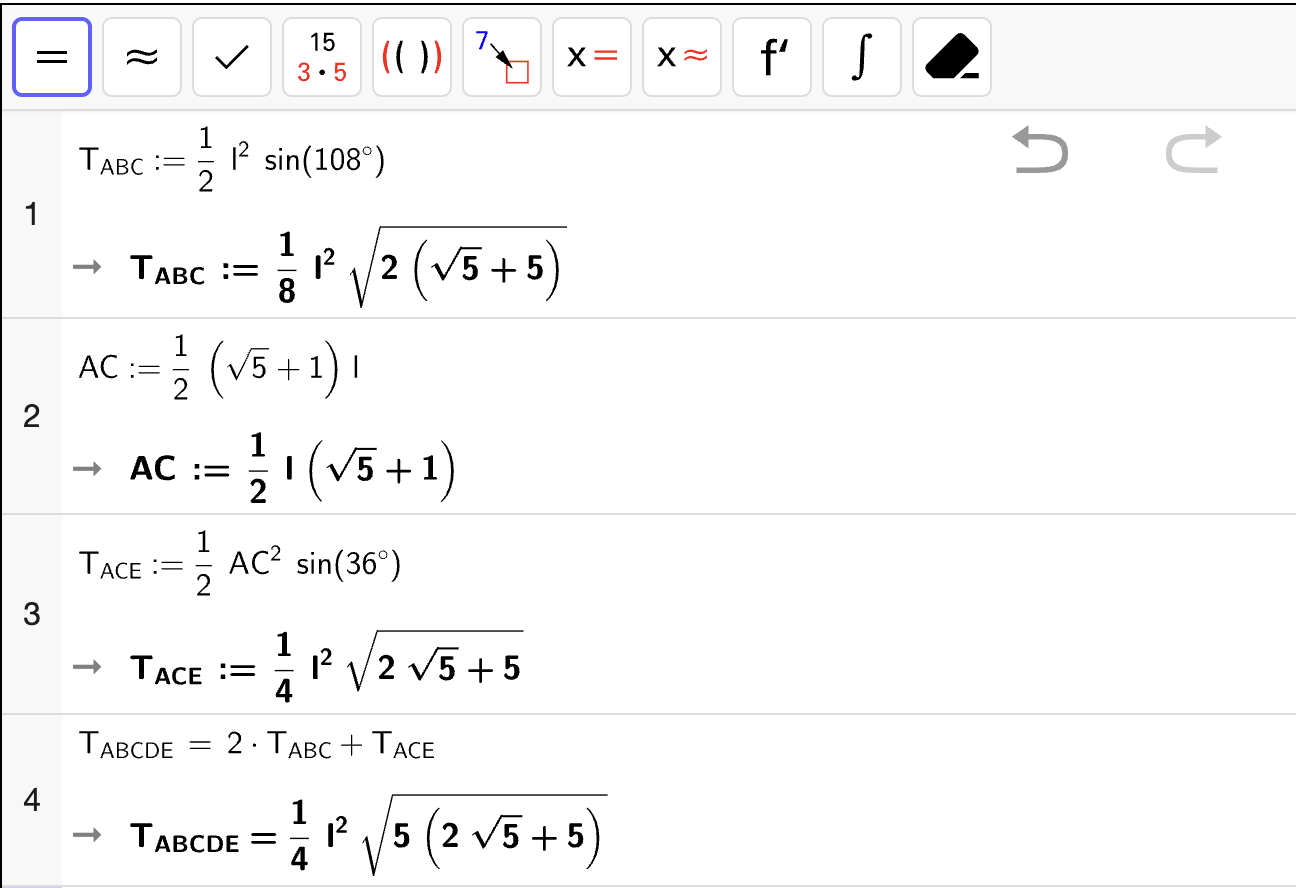
Bruk opplysningene ovenfor til å vise at funksjonen \(O\) gitt ved

\[ O(x) = -0.09x^2 + 51.04x - 2776.98 \]

er en god modell for hvor stort overskuddet en uke blir når kantinen produserer og selger \(x\) bagetter i løpet av uken.

Løsning

Vi bruker regresjon med en polynomfunksjon av grad \(2\) siden den oppgitte modellen er en andregradsfunksjon:

Vi kan altså se at

\[ O(x) = -0.09x^2 + 51.04x - 2776.98 \]

er en god modell ut ifra regresjonsanalysen og datapunktene vi har brukt.

b

Hvor mange bagetter må kantinen produsere og selge i løpet av en uke, ifølge modellen \(O\), for at overskuddet skal bli størst mulig?

Hvor stort blir dette overskuddet?

Løsning

Grafen til \(O\) vil ha et toppunkt siden \(O\) er en andregradsfunksjon og ledende koeffisient er negativ. Da vil overskuddet blir størst mulig når \(O'(x) = 0\). Vi løser likningen med CAS:

som betyr at \(O'(x) = 0\) når \(x \approx 283.56\). Kantina må derfor produsere og selges ca. 284 bagetter for at overskuddet skal bli størst mulig. Vi ser at overskuddet da er

\[ O(283.56) \approx 4459 \, \text{kr} \]

c

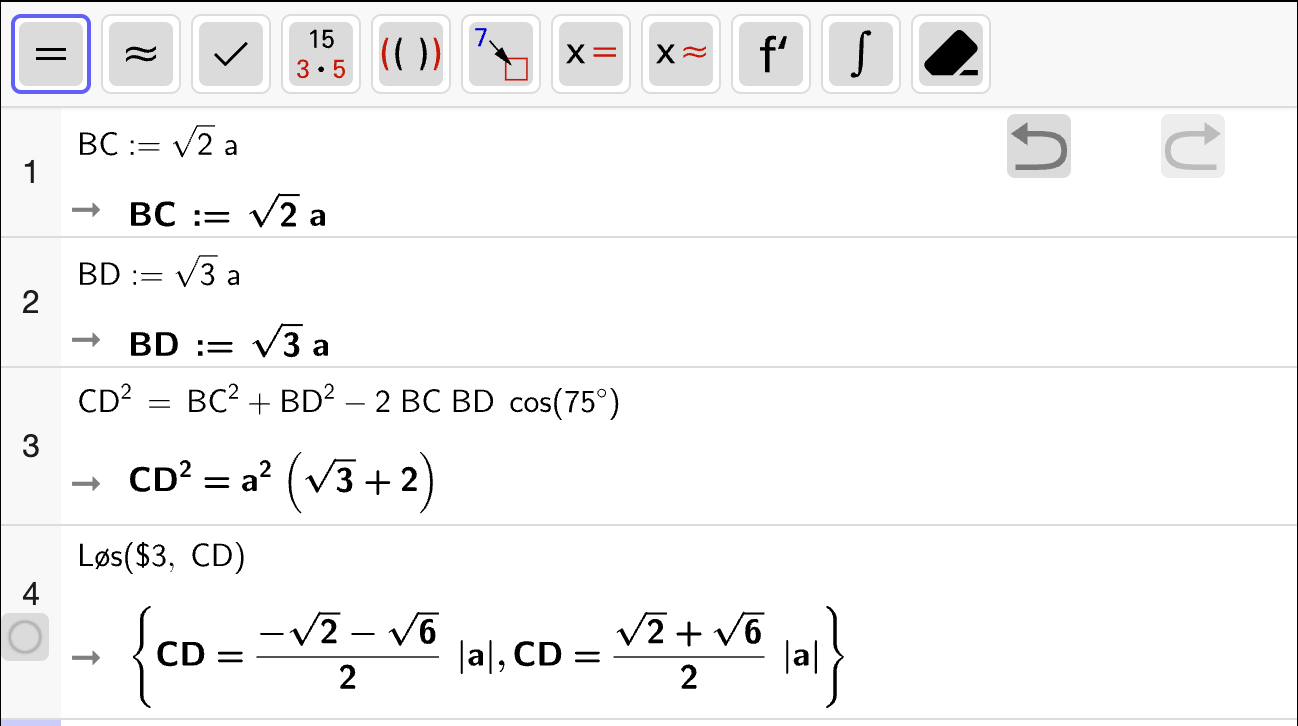
Bestem stigningstallet til den rette linjen som går gjennom punktene \((100, O(100))\) og \((200, O(200))\). Gi en praktisk tolkning av svaret du får.

Løsning

Vi bestemmer stigningstallet til linja gjennom punktene \((100, O(100))\) og \((200, O(200))\) ved å regne ut den gjennomsnittlige vekstfarten til \(O\) i intervallet \([100, 200]\). Dette gjør vi direkte med CAS:

som gir oss ca. 24 kr per bagett. Den praktiske tolkning av tallet er at dersom kantina øker antall bagetter de produserer og selger fra \(100\) til \(200\), så vil overskuddet øke med ca \(24\) kr per bagett i gjennomsnitt.

d

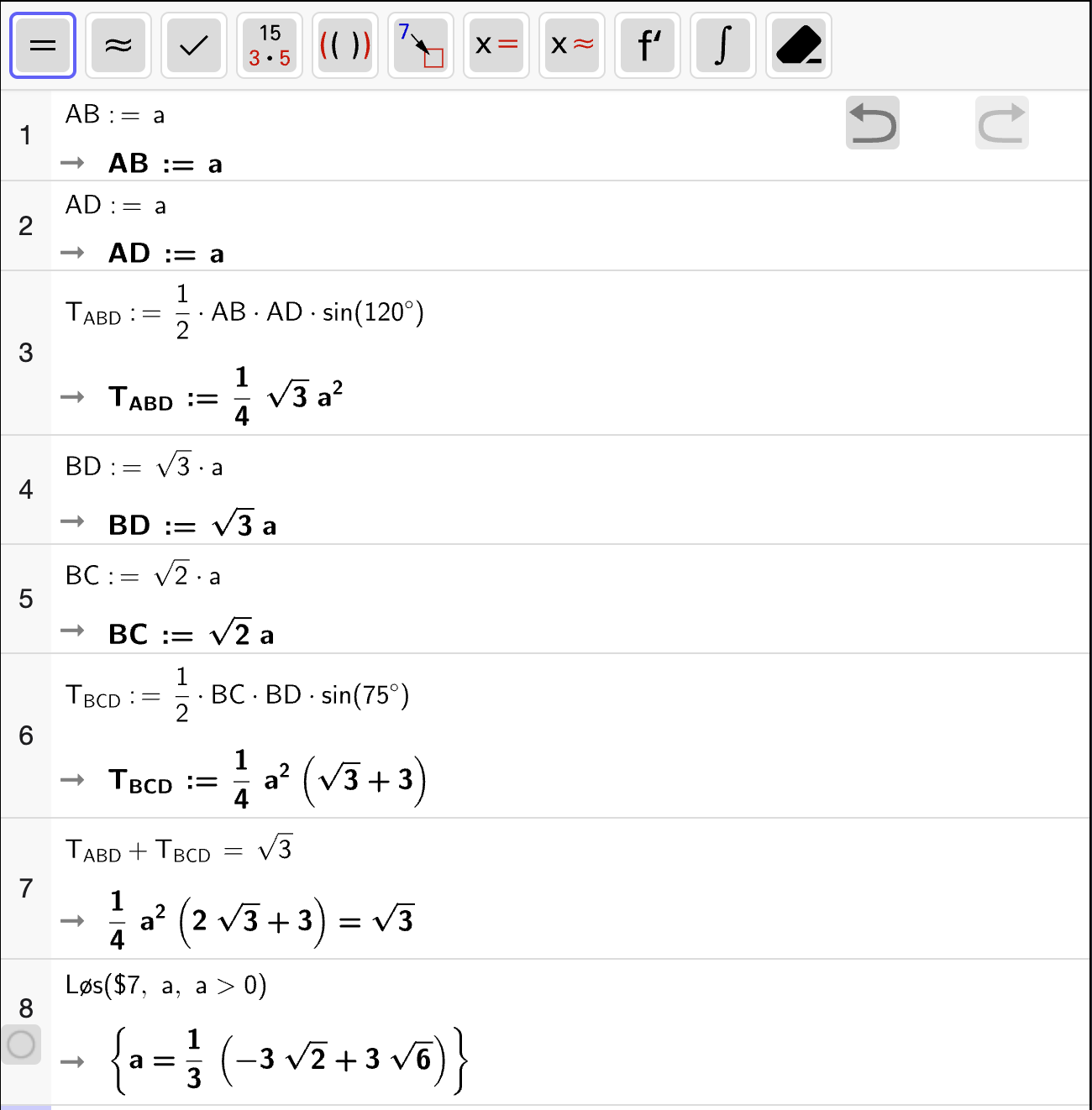
Bestem den momentane vekstfarten når \(x = 235\). Gi en praktisk tolkning av svaret du får.

Løsning

Den momentane vekstfarten til \(O\) i \(x = 235\) er \(O'(235)\). Vi regner ut dette med CAS:

som gir at \(O'(235) \approx 8.74\) kr per bagett. Den praktiske tolkningen av dette tallet er at dersom kantina øker antall bagetter de produserer og selger fra \(235\) til \(236\), så vil overskuddet øke med ca \(8.74\) kr.

---

Oppgave 2

Tabellen nedenfor viser antallet registrerte tilfeller av kikhoste i Norge noen måneder i perioden januar 2023 - oktober 2024.

Måned	Januar 2023	Mai 2023	Oktober 2023	Februar 2024	August 2024	Oktober 2024
Antall registrerte tilfeller	29	93	164	284	1035	1657

La \(x\) være antall måneder etter desember 2022, det vil si at \(x = 1\) tilsvarer januar 2023, \(x = 3\) tilsvarer mars 2023, og så videre.

a

Bruk opplysningene ovenfor til å vise at funksjonen \(K\) gitt ved

\[ K(x) = 27.8 \cdot 1.2^x \]

er en god modell for antall registrerte tilfeller av kikhoste i Norge i perioden januar 2023 - oktober 2024.

Løsning

Vi legger inn verdiene for \(x\) og \(K(x)\) i et regneark:

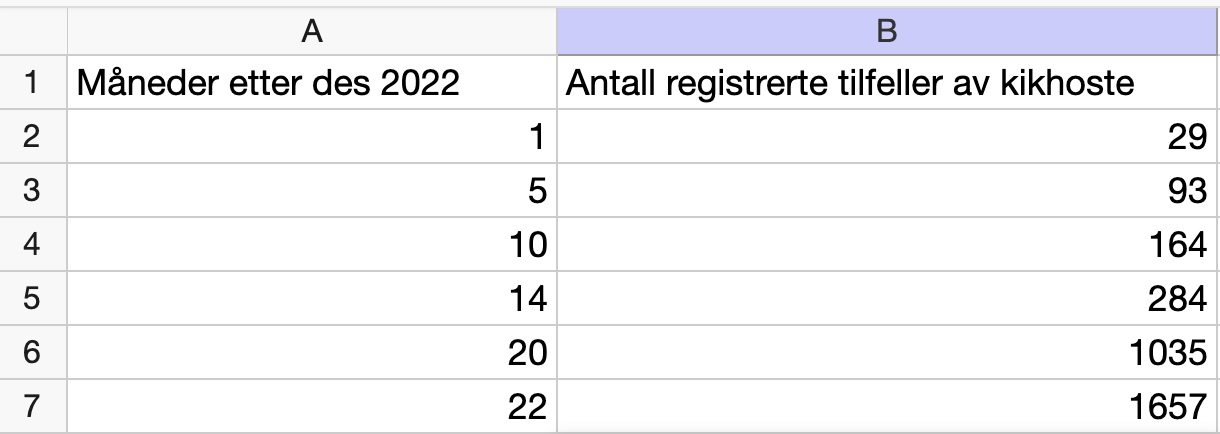
deretter utfører vi regresjon med en eksponentiell modell:

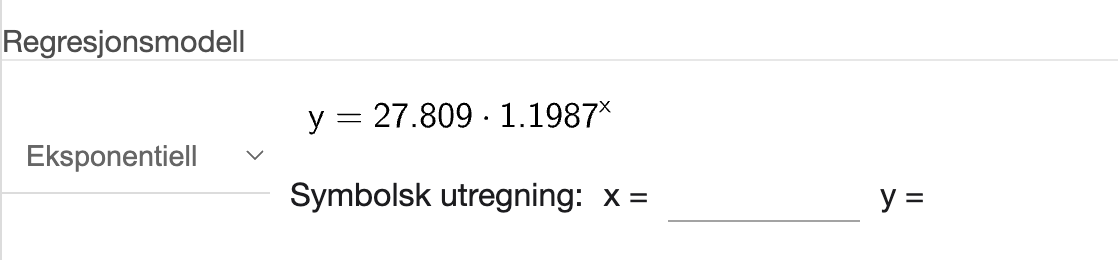
Fra skjermbilde ovenfor, kan vi se at modellen vi får er:

\[ K(x) = 27.809 \cdot 1.1987^x \approx 27.8 \cdot 1.2^x. \]

Dermed har vi vist at det oppgitte uttrykket for \(K(x)\) er en god modell for antall registrerte tilfeller av kikhoste i Norge i perioden januar 2023 - oktober 2024 der \(x\) er antall måneder etter desember 2022.

b

Bestem stigningstallet til den rette linjen som gjennom punktene \((4, K(4))\) og \((21, K(21))\).
Gi en praktisk tolkning av svaret du får.

Løsning

Vi bruker uttrykket for \(K(x)\) som er oppgitt i oppgaven. Stigningstallet til linja som går gjennom punktene \((4, K(4))\) og \((21, K(21))\) svarer til den gjennomsnittlige vekstfarten til \(K(x)\) i intervallet \([4, 21]\) som vi kan bestemme slik:

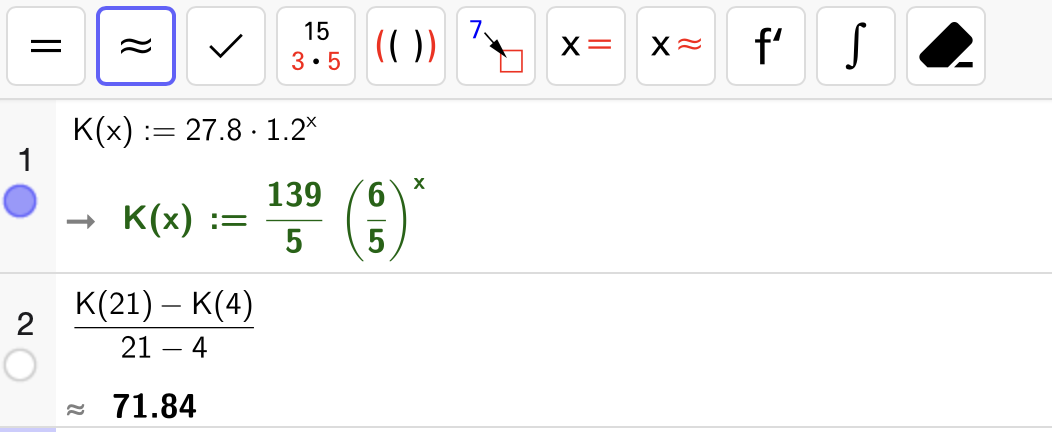
I celle 2 ser vi at stigningstallet er omtrent \(71.84\). Den praktiske tolkningen av dette er at antallet registrerte tilfeller av kikhoste økte i gjennomsnitt med ca. \(72\) tilfeller per måned i perioden fra april 2023 til september 2024 siden \(x = 4\) tilsvarer april 2023 og \(x = 21\) tilsvarer september 2024.

c

Hvor mange tilfeller av kikhoste vil bli registrert i Norge i mai 2025 ifølge modellen?

Fasit

Ifølge modellen blir det registrert omtrent \(5499\) tilfeller av kikhoste i Norge i mai 2025.

Løsning

Vi kan tolke problemet som at vi skal bestemme \(K(x)\) i mai 2025, som vi kan gjøre ved å sette

\[ x = \underbrace{5}_{\text{første mai måned}} + \underbrace{12}_{\text{antall måneder i et år}}\cdot \underbrace{2}_{\text{2 år senere}} = 29 \]

Vi regner ut med CAS:

Dermed vil modellen gi at antall registrerte tilfeller av kikhoste i Norge i mai 2025 er omtrent \(K(29) \approx 5499\).

---

Oppgave 3

En fabrikk har en vanntank. Vannet i tanken skal tappes ut.

Anta at funksjonen \(V\) gitt ved

\[ V(x) = 2000 - 2000\cdot \left(1 - \dfrac{x}{40}\right)^2 \, , \quad 0 \leq x \leq 40 \]

kan brukes som en modell for hvor mange liter vann \(V(x)\) som er tappet ut av tanken \(x\) minutter etter tappingen startet.

a

Bestem \(V(0)\). Gi en praktisk tolkning av svaret.

Løsning

Vi bestemmer \(V(0)\) ved å bruke CAS:

Altså er \(V(0) = 0\) som forteller oss at når vi setter i gang å tappe ut vann, så har vi tappet ut \(0\) liter med vann.

b

Bestem verdimengden til \(V\).

Fasit

\[ V(x) \in [0, 2000] \]

Løsning

Fra den praktiske situasjonen, vil det være naturlig at verdimengden er \(V(x) \in [0, V_\mathrm{maks}]\) for et maksimalt volum \(V_\mathrm{maks}\). For å bestemme dette kan vi regne ut verdien til \(V(x)\) i endepunktene \(x\in \{0, 40\}\). Vi regner ut for det sistenevnte punktet med CAS og finner:

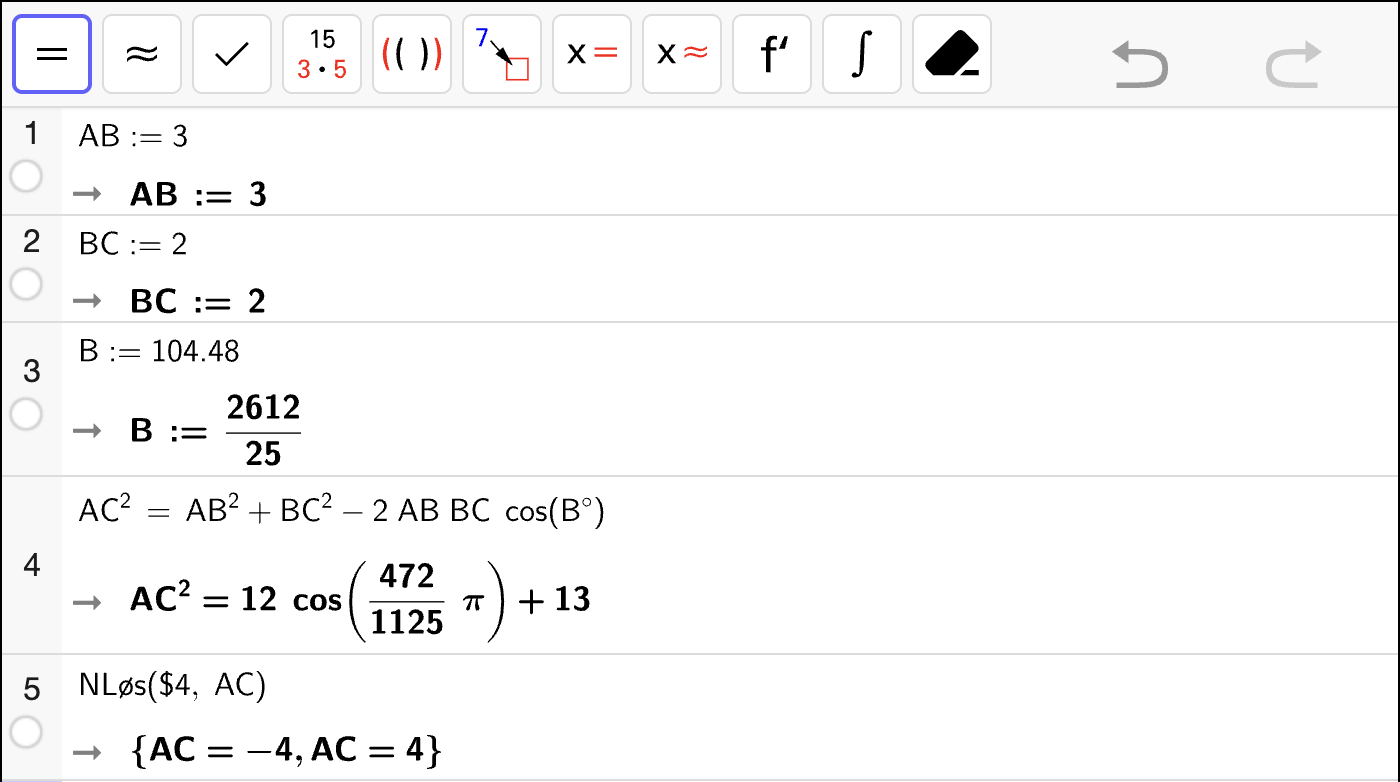
som betyr at \(V(0) = 0\) og \(V(40) = 2000\). Dermed vil verdimengden kunne beskrives som

\[ V(x) \in [0, 2000] \]

som forteller oss ta vi til sammen har 2000 liter med vann i tanken.

c

Hvor lang tid vil det ta før halvparten av vannet er tappet ut av tanken?

Fasit

\(11.72\) minutter.

Løsning

For å avgjøre hvor lang tid det tar før halvparten av vannet er tappet ut, løser vi likningen

\[ V(x) = \dfrac{2000}{2} = 1000 \]

siden vi fant at det til sammen var 2000 liter med vann i tanken i oppgave b. Vi løser likningen med CAS:

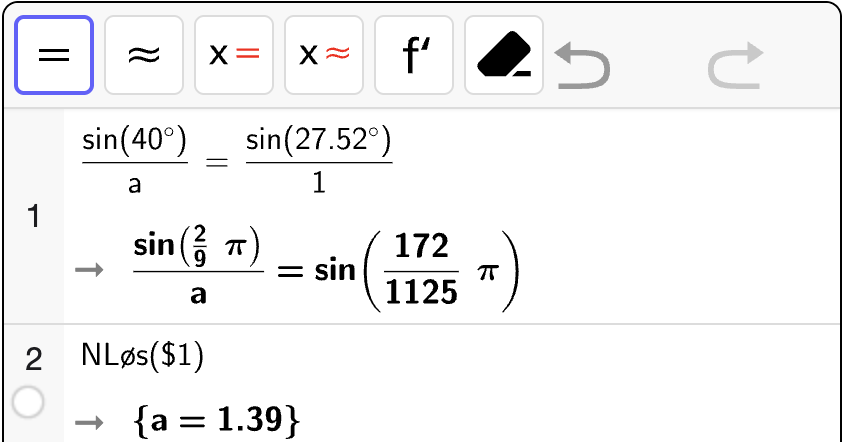
Her får vi to løsninger, men det er bare løsningen \(x \in [0, 40]\) som er meningsfull, som betyr at det tar \(11.72\) minutter før halvparten av vannet er tappet ut av tanken.

d

Bestem stigningstallet til den rette linjen som går gjennom punktene \((0, V(0))\) og \((30, V(30))\). Gi en praktisk tolkning av svaret du får.

Fasit

\(62.5\) liter per minutt tappes ut i gjennomsnitt de første 30 minuttene av tappingen.

Løsning

Stigningstallet til den rette linjen gjennom \((0, V(0))\) og \((30, V(30))\) svarer til den gjennomsnittlige vekstfarten til \(V(x)\) i intervallet \([0, 30]\). Vi regner ut dette med CAS:

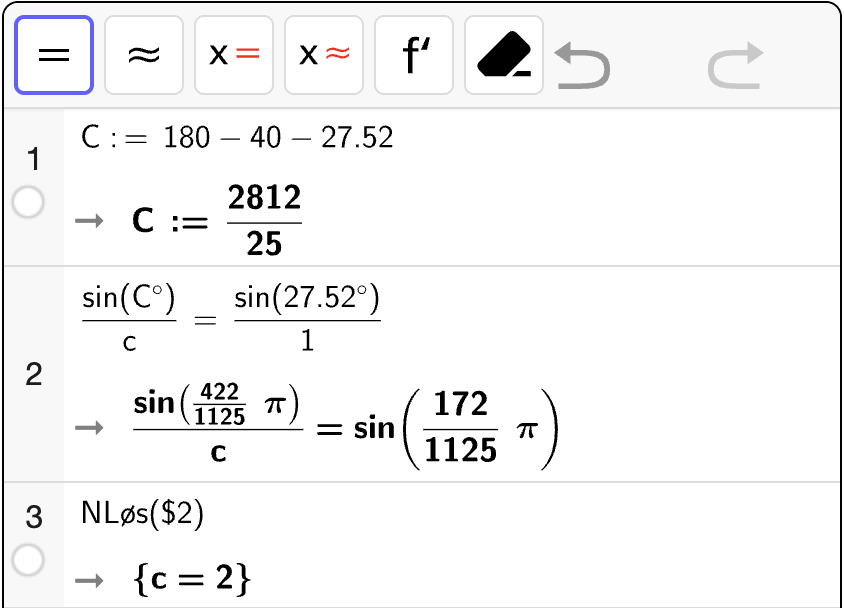
som betyr at stigningstallet til linja er \(62.5\) liter per minutt. Den praktiske tolkningen av svaret er at det tappes ut \(62.5\) liter per minutt i gjennomsnitt de første 30 minuttene av tappingen.

e

Undersøk om det noen gang vil tappes ut mer enn 105 liter vann i løpet av ett minutt.

Løsning

Den praktiske tolkningen av den momentane vekstfarten \(V'(x)\) er at den forteller oss omtrent hvor mye volumet med vann endrer dersom vi øker verdien av \(x\) med \(1\). Med andre ord

\[ V'(x) \approx V(x + 1) - V(x) \]

som betyr at det er tilnærmet verdi for hvor mye vann som tappes ut i løpet av ett minutt. Siden spørsmålet handler om det tappes ut mer enn \(105\) liter, betyr det at vi lurer på om

\[ V'(x) < -105 \]

for noen \(x \in [0, 40]\). Vi løser ulikheten med CAS:

\[ V'(x) < -105 \liff x > 82 \]

som ikke ligger innenfor definisjonsmengden. Med andre ord finner vi at det aldri tappes ut mer enn \(105\) liter vann i løpet av ett minutt.

---

Oppgave 4

En gruppe statistikere har sett på hvordan folketallet i et område har endret seg siden 1960, og laget en modell \(F\) gitt ved

\[ F(x) = \dfrac{1}{1000}\cdot \left(0.027 x^3 - 5.8 x^2 + 220x + 7900\right), \quad x \in [0, 80] \]

for folketallet \(F(x)\) tusen innbyggere i området \(x\) år etter 1960.

a

Vis hvordan du på to ulike måter kan bestemme når folketallet var høyest ifølge modellen.

Løsning

Metode 1: Løse \(F'(x) = 0\)
Siden løsningene av \(F'(x) = 0\) gir ekstremalpunktene som vil være punkter når folketallet enten er lavest eller høyest, kan vi løse denne likningen for å avgjøre når folketallet var høyest. Vi gjør dette med CAS:

Her får vi to kandidater

\[ x \approx 22.5 \or x \approx 120.71. \]

Men kun den første kandidaten ligger innenfor definisjonsmengden \(D_F = [0, 80]\). Vi kan undersøke om det er toppunkt ved å regne ut \(F(x)\) i to “nabopunkter” til \(x = 22.5\) og sjekker om \(F(22.5)\) er større enn begge. Vi gjør utregningen med CAS:

som forteller oss at

\[ F(22.5) > F(20) \and F(22.5) > F(25) \]

så \(x = 22.5\) svarer til et toppunkt. Dermed er det høyeste folketallet i området \(x = 22.5\) år etter 1960 som tilsvarer i år 1982.

Metode 2: Finne toppunktet grafisk
Vi kan også bruke den grafiske representasjonen til \(F\) og bestemme toppunktet med en graftegner. Se figuren nedenfor.

Fig. 31.1 viser grafen til \(F\) der \(y\)-aksen viser folketallet i tusen innbyggere og \(x\)-aksen viser antall år etter 1960.

Her har vi brukt følgende kommando i Geogebra for å bestemme koordinatene til toppunktet:

som forteller oss at koordinatene til toppunktet er \((22.5, 10.22)\) som betyr at folketallet var høyest når \(x = 22.5\) år etter 1960 som tilsvarer i år 1982.

b

Bestem stigningstallet til den rette linjen som går gjennom punktene \((30, F(30))\) og \((70, F(70))\). Gi en praktisk tolkning av dette stigningstallet.

Løsning

Stigningstallet til den rette linjen som går gjennom \((30, F(30))\) og \((70, F(70))\) er den gjennomsnittlige vekstfarten til \(F\) i intervallet \([30, 70]\). Vi regner ut dette med CAS:

Vi ser at stigningstallet til linja er ca. \(-0.15\) som betyr at folketallet synker med ca. \(150\) innbyggere per år i gjennomsnitt i perioden fra 1990 til 2030, iføle modellen.

c

Når vil folketallet avta raskest ifølge modellen?

Løsning

Folketallet vil avta raskest når den momentane vekstfarten \(F'(x)\) er minst mulig og negativ. Vi må altså lete etter bunnpunktet til \(F'(x)\). Vi kan gjøre dette ved å løse likningen \(F''(x) = 0\). Det vil si, vi deriverer den deriverte \(F'\) for å finne ut hvor mye \(F'\) endrer seg, og så finner vi bunnpunktet til \(F'\) for å bestemme når \(F''(x) = 0\). Vi gjør dette med CAS:

som betyr at når \(x \approx 71.6\), altså i år 2031, vil folketallet avta raskest ifølge modellen. Vi kan være sikre på at dette er punktet hvor \(F'(x)\) er minst mulig og negativ fordi grafen til \(F\) synker mest her ved å referere tilbake til grafen til \(F\) fra oppgave a. Grafen til \(F\) synker etter at \(x = 22.5\) frem til \(x = 80\) og \(F'(x)\) er negativ i hele dette intervallet. Tangenten til grafen til \(F\) vil være “brattest” i \(x = 71.6\), og siden stigningstallet er negativt, vil det svare til når folketallet avtar raskest ifølge modellen.

---

Oppgave 5

Funksjonen \(P\) gitt ved

\[ P(x) = 3600 \cdot 0.85^x + 600 \]

er en modell som viser hvor mange personer som abonnerte på papirutgaven av en avis \(x\) år etter 2010.

a

Vis hvordan du på to ulike måter kan finne ut hvor mange person som abonnerte på papirutgaven av avisen i 2010.

Løsning

1. Metode 1: Regne ut \(P(0)\)
   Vi kan bruke funksjonsuttrykket og regne ut \(P(0)\) siden \(x = 0\) tilsvarer å 2010. Vi bruker CAS til å utføre dette:

2. Metode 2: Finne skjæringen med \(y\)-aksen
   Vi bruker den grafiske representasjonen til \(P\) og bestemmer skjæringen med \(y\)-aksen med en graftegner. Se figuren nedenfor.

I utgangspunktet bruker vi bare kommandoen:

som forteller oss at punktet \((0, 4200)\) ligger på grafen til \(P\). Dermed er det 4200 personer som abonnerte på papirutgaven når \(x = 0\) som tilsvarer i år 2010.

b

Bestem stigningstallet til den rette linjen som går gjennom punktene \((4, P(4))\) og \((14, P(14))\). Gi en praktisk tolkning av svaret du får.

Løsning

Stigningstallet til den rette linjen som går gjennom \((4, P(4))\) og \((14, P(14))\) er den gjennomsnittlige vekstfarten til \(P\) i intervallet \([4, 14]\). Vi regner ut dette med CAS:

Altså er stigningstallet til linja ca. \(-151\). Den praktiske tolkningen er at antall abonnenter papirutgaven av avisen synker med 151 abonnenter per år i gjennomsnitt, i perioden fra 2014 til 2024.

c

Bestem den momentane vekstfarten når \(x = 10\). Gi en praktisk tolkning av svaret du får.

Løsning

Den momentane vekstfarten til \(P\) når \(x = 10\), er gitt ved \(P'(10)\). Vi regner ut dette med CAS:

som betyr at

\[ P'(10) \approx -116 \]

Den praktiske tolkningen av dette tallet er at det er det blir ca. 116 færre abonnenter fra år \(x = 10\) til \(x = 11\) som betyr at i løpet av år 2020, så vil det være ca. 116 person som kansellerer abonnementet sitt på papirutgaven av avisen.

d

I 2019 abonnerte 1000 personer på den digitale utgaven av avisen. Antallet personer som abonnerte på den digitale utgaven, økte med \(5.5 \%\) hvert år fra 2019 til 2024.

I hvilket år var det for første gang flere personer som abonnerte på den digitale utgaven av avisen enn på papirutgaven?

Løsning

Vi kan sette opp en modell \(D\) som gir antall abonnenter \(D(t)\) på den digitale utgaven \(t\) år etter 2019 slik at \(t = 0\) svarer til år 2019. Siden det er prosentvis økning på \(5.5 \%\) per år fra en startverdi på \(1000\) abonnenter i 2019, vil modellen være en eksponentiell modell på formen

\[ D(t) = \underbrace{1000}_{\text{startverdi}} \cdot \underbrace{1.055^t}_{\mathrm{vekstfaktor}} \]

For å kunne sammenligne \(D(t)\) med \(P(x)\), er det hjelpsomt å bytte variabel i én av modellene så vi kan sammenligne funksjonsverdiene direkte. Her kan vi for eksempel bytte variabel i \(D(t)\) til \(x\) slik at vi får en modell \(D(x)\) som gir antall abonnenter på den digitale utgaven av avisen \(x\) år etter 2010. Men samtidig må vi huske på at denne modellen kun er gyldig fra og med år 2019, altså når \(x \geq 9\). Det betyr at vi kan skrive sammenhengen mellom \(t\) og \(x\) som

\[ t = x - 9 \]

så lenge \(x \geq 9\) siden \(x = 9\) vil gi \(t = 0\), \(x = 10\) vil gi \(t = 1\) osv.

Da kan vi skrive om \(D(t)\) til \(D(x)\) ved å bytte variabelen slik vi har definert over:

\[ D(x) = 1000 \cdot 1.055^{x - 9} \]

der modellen kun gir mening for \(x \geq 9\) siden dette er fra og med år 2019. Med denne modellen, kan vi nå undersøke når antall papirabonnenter \(P(x)\) er mindre enn antall digitale abonnenter \(D(x)\) ved å løse ulikheten

\[ P(x) < D(x) \]

som vi gjør med CAS:

Altså vil antall papirabonnenter bli lavere enn antall digitale abonnenter når \(x > 11.58\) som betyr at det i løpet av år 2021 blir flere digitale abonnenter enn papirabonnenter.

---

---

Oppgave 6

Lufttrykk måles ofte i hektopascal (hPa). Jo høyere over havet vi befinner oss, jo lavere er lufttrykket. Lufttrykket ved havets overflate er ca. 1000 hPa.

Når lufttrykket er lavere enn 1000 hPa, vil kokepunktet for vann være lavere enn \(100 \degree \mathrm{C}\). Se tabellen nedenfor.

Lufttrykk \(\left(\mathrm{hPa}\right)\)	Kokepunkt for vann \(\left(\degree \mathrm{C}\right)\)
\(1000\)	\(100\)
\(500\)	\(81.4\)
\(200\)	\(60.1\)
\(80\)	\(41.5\)
\(40\)	\(29\)

a

Bestem en modell \(K\) på formen

\[ K(x) = a \cdot x^b \]

som tilnærmet viser sammenhengen mellom lufttrykket \(x\) hPa og kokepunktet \(K(x) \, \degree \mathrm{C}\).

Løsning

Først fyller vi inn datapunktene i et regneark:

deretter bruker vi regresjonsanalyse og velger potens som modellklasse:

Modellen vår \(K\) er derfor gitt ved

\[ K(x) = 7.56 \cdot x^{0.38} \]

b

Nedenfor vises en samtale mellom to elever.

Ari

Et egg blir ikke hardkokt dersom temperaturen i vannet er lavere enn \(85 \, \degree\mathrm{C}\). Betyr det at det ikke går an å få egg hardkokte på et høyt fjell?

Lisa

Det kommer vel an på hvor høyt fjellet er?

Ari

Jeg vil lage en modell som viser hvor høyt lufttrykket er \(x\) kilometer over havets overflate. Jeg har lært at lufttrykket minker med ca. \(12 \, \%\) per km.

Lisa

Jeg har lært at lufttrykket halveres for hver \(5.5\) km. Jeg vil ta utgangspunkt i dette og lage en modell på samme form som den du lager, Ari.

Lag modellen til Ari og Lisa.

Løsning

Modellen til Ari er en eksponentiell modell der vekstfaktoren er \(0.88\) siden det er \(12 \%\) nedgang per kilometer. Vi kaller modellen for \(A\). Da har vi at

\[ A(x) = 1000 \cdot 0.88^x \]

siden \(x\) er antall kilometer over havet og lufttrykket er \(1000 hPa\) ved havnivå.

Modellen til Lisa er også en eksponentiell modell der vi vet at lufttrykket halveres for hver \(5.5\) km. Vi lar \(L\) være modellen til Lisa. Da har vi at

\[ L(x) = 1000 \cdot b^x \]

Siden lufttrykket halveres for hver \(5.5\) km, betyr det at

\[ L(5.5) = 500. \]

Vi må bestemme \(b\) slik at dette stemmer. Vi gjør det med CAS:

Vi ser at \(b \approx 0.88\) akkurat som i Ari sin modell. Det er altså ingen nevneverdig forskjell mellom de to modellene, de er bare beskrevet på forskjellig måte.

c

Omtrent hvor høyt over havet er det mulig å få egg hardkokte?

Løsning

Vi finner først ut hvilket lufttrykk \(x\) som gir \(K(x) = 85\). Vi løser likningen med CAS:

som betyr at vi må ha et lufttrykk på omtrent \(574.76\) hPa. Vi kan så bestemme ved hvilken høyde over havet dette lufttrykket er ved å bruke Ari sin modell i CAS:

som forteller oss at kokepunktet er på \(85 \degree \mathrm{C}\) når vi er omtrent \(4.3\) km over havet. Dermed er dette den størst høyden vi kan være på for å kunne lage hardkokte egg.

---

Oppgave 7

Åpne CAS‑vindu

En båt skal reise fra en øy \(A\) til en øy \(C\).
Båten skal kjøre innom land på en kystlinje på et punkt \(B\) for å hente ferskvann. Punktet kan være hvor som helst langs kystlinjen. Båten skal reise en så kort som mulig avstand for å spare drivstoff.

Kystlinjen er \(9\) km lang. Øy \(A\) ligger \(2\) km fra land og øy \(C\) ligger \(4\) km fra land. Se figuren nedenfor.

En strandkiosk \(S\) er plassert på starten av kystlinja.

a

Bestem lengden båten må kjøre fra \(A\) til \(C\) dersom den går i land \(1\) km fra strandkiosken.

b

Lag en modell \(L\) som gir lengden \(L(x)\) som båten må kjøre dersom den går i land en avstand \(x\) fra strandkiosken.

c

Bestem hvor langt unna strandkiosken båten må gå i land for å få kortest mulig reisevei fra \(A\) til \(C\).

---

Oppgave 8

En sylinder med et hull i bunnen vil tappe ut vann når hullet er åpent.

Den horisontale avstanden vannstrålen beveger seg \(S\) meter når vannstanden er \(x\) meter over bunnen av sylinderen. I tabellen nedenfor vises et datamateriale for dette.

\(x\) (meter)	\(8\)	\(6\)	\(5\)	\(3\)	\(2\)
\(S\) (meter)	\(5.66\)	\(4.90\)	\(4.47\)	\(3.46\)	\(2.83\)

a

Lag en modell på formen

\[ S(x) = a \cdot x^b \]

som viser hvor mange meter \(S(x)\) vannstrålen beveger seg horisontalt når vannstanden er \(x\) meter over bunnen av sylinderen.

b

Etter at hullet ble åpnet, varierte høyden til vannstanden med tiden slik at den kan beskrives av en modell på formen

\[ h(t) = k\cdot(t - r)^2 \]

Når hullet i bunnen ble åpnet var vannstanden \(10\) meter over bunnen. Tanken ble halvfull etter \(7\) sekunder.

Bestem \(k\) og \(r\). Gi en praktisk tolkning av konstanten \(r\).

c

Hvor lang tid tar det før lengden av strålen og høyden på vannstanden er like?

---

Oppgave 9

Anna skal reise fra en holme som ligger \(8\) km fra strandkanten. \(12\) km fra det punktet på stranden som ligger nærmest holmen, ligger det en hytte. Se figuren nedenfor.

Anna kan ro med en fart på \(2\) km/t og gå med en fart på \(6\) km/t.

a

Bestem hvor lang tid Anna bruker til hytta dersom hun ror i land \(6\) km fra det punktet på stranden som ligger nærmest holmen.

Fasit

\[ T = 6 \, \mathrm{t} \]

Løsning

Vi bruker Pytagoras’ setning til å regne ut hvor langt Anna må ro for å komme i land \(6\) km fra det punktet på stranden som ligger nærmest holmen. Da får vi at:

\[ L_\mathrm{robåt} = \sqrt{6^2 + 8^2} \, \mathrm{km} = \sqrt{100} \, \mathrm{km} = 10 \, \mathrm{km}. \]

Siden Anna ror med en fart på \(2\) km/t, bruker hun tiden

\[ T_\mathrm{robåt} = \frac{L_\mathrm{robåt}}{2 \, \mathrm{km/t}} = \frac{10 \, \mathrm{km}}{2 \, \mathrm{km/t}} = 5 \, \mathrm{t} \]

til å ro til stranden. Hun må deretter gå \(12 - 6 = 6\) km til hytta. Siden hun går med en fart på \(6\) km/t, bruker hun tiden

\[ T_\mathrm{gåtur} = \frac{6 \, \mathrm{km}}{6 \, \mathrm{km/t}} = 1 \, \mathrm{t} \]

til å gå til hytta. Den totale tiden hun bruker til hytta blir derfor

\[ T = T_\mathrm{robåt} + T_\mathrm{gåtur} = 5 \, \mathrm{t} + 1 \, \mathrm{t} = 6 \, \mathrm{t}. \]

b

Lag en modell \(T\) som viser mange timer \(T(x)\) Anna bruker på å reise til hytta dersom hun ror i land \(x\) km fra det punktet på stranden som ligger nærmest holmen.

Fasit

\[ T(x) = \dfrac{\sqrt{x^2 + 6^2}}{2} + \dfrac{12 - x}{6} \]

Løsning

Hvis Anna ror i land \(x\) km fra det punktet på stranden som ligger nærmest holmen, må hun ro en avstand på

\[ L_\mathrm{robåt}(x) = \sqrt{x^2 + 8^2} \]

Anna ror med en fart på \(2\) km/t, så tiden hun bruker til å ro blir

\[ T_\mathrm{robåt}(x) = \frac{L_\mathrm{robåt}(x)}{2} = \frac{\sqrt{x^2 + 8^2}}{2}. \]

Siden avstanden er 12 km fra punktet på strandlinja nærmest holmen bort til hytta, så må hun gå

\[ L_\mathrm{gåtur}(x) = 12 - x \]

kilometer til hytta. Anna går med en fart på \(6\) km/t, så tiden hun bruker til å gå blir

\[ T_\mathrm{gåtur}(x) = \frac{L_\mathrm{gåtur}(x)}{6} = \frac{12 - x}{6}. \]

Dermed vil en modell for tiden Anna bruker til hytta når hun ror i land \(x\) km fra det punktet på stranden som ligger nærmest holmen være gitt ved

\[ T(x) = T_\mathrm{robåt}(x) + T_\mathrm{gåtur}(x) = \frac{\sqrt{x^2 + 8^2}}{2} + \frac{12 - x}{6}. \]

c

Bestem hvor Anna må gå i land for at hun skal bruke minst mulig tid på å reise til hytta.
Hva er den kortest tiden Anna kan bruke?

Fasit

• Anna må gå i land ved \(x \approx 2.83 \, \mathrm{km}\) for å få kortest mulig reisetid.

• Anna bruker da \(T \approx 5.77 \, \mathrm{t}\) på reisen.

Løsning

For å finne ut hvor Anna må gå i land for at hun skal bruke minst mulig tid på å reise til hytta, løser vi likningen \(T'(x) = 0\) med CAS for å finne \(x\)-koordinaten til et eventuelt bunnpunkt for \(T\):

Dermed vil Anna bruke minst mulig tid dersom hun går i land ved

\[ x = 2 \sqrt{2} \, \mathrm{km} \approx 2.83 \, \mathrm{km}. \]

Da bruker hun ca. \(5.77\) timer på reisen.

Vi bør dobbeltsjekke at dette svarer til et bunnpunkt ved å regne ut \(T(x)\) i endepunktene og sjekke at verdiene vi får er høyere:

• Hvis Anna ror båten direkte til nærmeste punkt på stranden, bruker hun \(T(0) = 6\) timer.

• Hvis Anna ror båten hele veien til hytta, bruker hun \(T(12) \approx 7.21\) timer.

Konklusjon:

• Anna må gå i land ved \(x \approx 2.83 \, \mathrm{km}\) for å få kortest mulig reisetid.

• Anna bruker da \(T \approx 5.77 \, \mathrm{t}\) på reisen.

---

Oppgave 10

Åpne CAS‑vindu

En takrenne skal lages i form av et åpent trapes ved å brette to sidekanter fra et flatt rektangel slik at alle sidelengder i takrenna er \(10\) cm og takrennen har en høyde på \(x\) cm. Se figuren nedenfor.

a

Bestem tverrsnittsarealet \(T\) av takrenna dersom høyden av takrenna er \(6\) cm.

Fasit

\[ T = 60 \, \mathrm{cm^2}. \]

b

Lag en modell \(T\) som gir tverrsnittsarealet \(T(x)\) i \(\mathrm{cm}^2\) når takrenna er \(x\) cm høy.

Fasit

\[ T(x) = 10x + x\sqrt{100 - x^2} \]

c

Bestem hvilken høyde som lar mest mulig vann strømme gjennom takrenna til enhver tid.

Fasit

\[ x = 5\sqrt{3} \, \mathrm{cm} \approx 8.66 \, \mathrm{cm} \]

---

Oppgave 11

Else skal gjerde inn tre områder for å lage en grønnsakshage. Det største området skal ha form som et rektangel og de to minste som likebeinte rettvinklede trekanter. Se figuren ovenfor.

Else skal sette opp gjerde langs alle linjestykkene vist i figuren ovenfor.
Hun har til sammen 100 m gjerde som hun vil bruke.

a

Hvor stor blir arealet av grønnsakhagen dersom hun velger at katetene i trekantene skal være \(8\) meter?

Fasit

\[ A = 245.5 \, \mathrm{m}^2 \]

Løsning

Først må vi bestemme hvor lange linjestykkene \(y\) i figuren er. Vi vet at \(x = 8\) meter. Til sammen summerer linjestykkene til \(L = 100\) meter. Vi kan skrive den samlede lengden av linjestykkene som

\[ L = \underbrace{2x}_{\mathrm{kateter}} + \underbrace{2x + 2y}_{\mathrm{rektangel}} + \underbrace{2\sqrt{2}x}_{\mathrm{hypotenuser}} = 100 \]

der vi har brukt Pytagoras’ setning til å finne at begge hypotenusene i de rettvinklede trekantene må være

\[ h^2 = x^2 + x^2 \limplies h = \sqrt{2}x. \]

Vi kan først løse likningen for \(y\) slik at vi kan regne ut \(y\) for en hver verdi av \(x\):

\[ 4x + 2y + 2\sqrt{2}x = 100 \liff 2x + y + \sqrt{2}x = 50 \]

som gir

\[ y = 50 - (2 + \sqrt{2})x. \]

Det samlede arealet til grønnsakhagen blir

\[\begin{align*} A &= A_{\mathrm{rektangel}} + 2A_{\mathrm{trekant}} \\ \\ &= xy + 2 \cdot \frac{1}{2}x^2 \\ \\ &= x\left(50 - (2 + \sqrt{2})x\right) + x^2 \\ \\ &= 50x - (2 + \sqrt{2})x^2 + x^2 \\ \\ &= 50x - (1 + \sqrt{2})x^2 \end{align*}\]

Vi kan definere en funksjon \(A(x)\) i CAS og regne ut arealet for \(x = 8\):

som betyr at arealet av grønnsakhagen er omtrent \(A = 245.5 \, \mathrm{m}^2\) dersom katetene i trekantene er \(8\) meter lange.

b

Lag en oversikt som viser hvordan arealet av grønnsakhagen endrer seg dersom hun velger andre lengder på katetene. Av oversikten skal Else kunne se omtrent hvor lange katetene må være for at arealet av grønnsakhagen skal bli størst mulig.

Løsning

Vi bruker en grafisk framstilling av arealet \(A(x)\) for å se hvordan arealet endrer seg med lengden på katetene. Vi kan bruke Geogebra-vinduet til å lage grafen til \(A\) siden vi allerede har definert \(A(x)\) i CAS.

Fig. 31.2 viser en grafisk fremstilling av arealet \(A(x) \, \mathrm{m}^2\) på \(y\)-aksen når katetene i trekanten er \(x\) meter lange.

Fra den grafiske framstillingen kan vi se at arealet er størst når katetene i trekanten er omtrent \(x = 10\) meter lange fordi dette svarer til et toppunkt på grafen til \(A\).

c

Lag en modell \(A\) som Else kan bruke for å regne ut arealet \(A(x)\) av grønnsakhagen for ulike verdier av \(x\).

Fasit

\[ A(x) = 50x - (1 + \sqrt{2})x^2. \]

Løsning

Vi har allerede laget denne modellen i oppgave a som er gitt ved

\[ A(x) = 50x - (1 + \sqrt{2})x^2. \]

d

Bruk modellen til å finne den lengden av katetene som vil gi det største arealet.

Fasit

\[ x = (25\sqrt{2} - 25) \, \mathrm{m} \approx 10.36 \, \mathrm{m}. \]

Løsning

For å bestemme den kateten som gir størst mulig areal, bruker vi CAS og løser \(A'(x) = 0\) for å bestemme \(x\)-koordinaten til toppunktet til \(A\):

som betyr at arealet er størst når katetene i trekantene er

\[ x = (25\sqrt{2} - 25) \, \mathrm{m} \approx 10.36 \, \mathrm{m}. \]

Men vet vi at dette er et toppunkt? Ja, for den ledende koeffisienten til \(A(x)\) er negativ, så vi legger’n død – og vi hadde strengt tatt grafen som viste det i oppgave b også.

e

Bestem modellens gyldighetsområde.

Fasit

\[ 0 < x < \dfrac{50}{\sqrt{2} + 2} \]

Løsning

Modellen er gyldig så lenge \(A(x) > 0\) og \(y > 0\). Vi løser den første ulikheten i CAS:

Altså er \(A(x) > 0\) når

\[ x \in \left\langle 0, 50 \sqrt{2} - 50 \right\rangle. \]

Men vi må også sjekke at \(y > 0\). Fra a vet vi at

\[ y = 50 - (2 + \sqrt{2})x \]

så vi løser ulikheten \(y > 0\) i CAS:

Kombinerer vi de to løsningene, ser vi at modellen er gyldig så lenge

\[ 0 < x < \dfrac{50}{\sqrt{2} + 2} \]

---

Oppgave 12

Isabel er industridesigner. Hun arbeider med et design på bokser med form som sylindre.

Formel for å regne ut volumet av en boks med radius \(r\) og høyde \(h\) er

\[ V = \pi \cdot r^2 \cdot h \]

Formel for å regne ut arealet av overflaten av boksen er

\[ O = \pi \cdot r^2 + 2\cdot \pi \cdot r \cdot h \]

Isabel lurer på hvor stor radius hun bør velge og hvor høye boksene må være, når hver boks skal ha

• et volum \(V\) på \(450 \, \mathrm{cm}^3\)

• minst mulige overflate \(O\)

Isabel ser at når hun har gitt volum og radius, kan hun regne ut høyden ved å bruke formelen \(V = \pi \cdot r^2 \cdot h\)

a

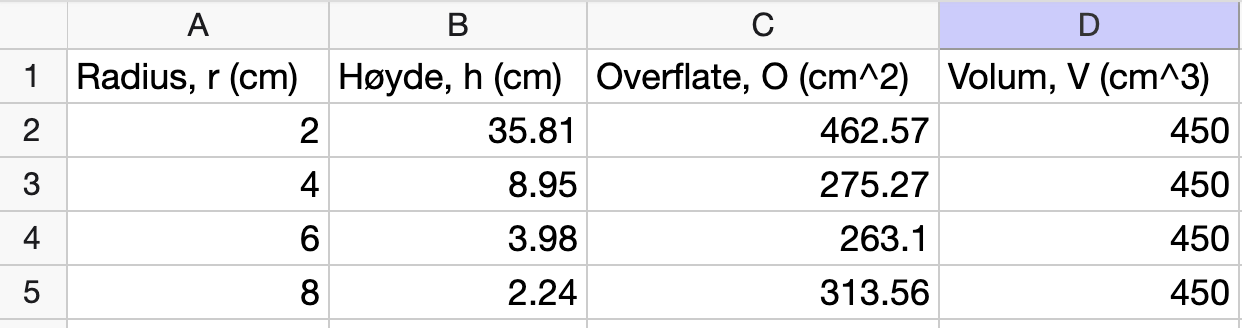
Lag en oversikt som vist nedenfor. Gjør beregninger og fyll inn verdiene som mangler.

Radius, \(r\) (cm)	Høyde, \(h\) (cm)	Overflate, \(O\) (cm\(^2\))	Volum, \(V\) (cm\(^3\))
2	35.8	462.6	450
4			450
6			450
8			450

Løsning

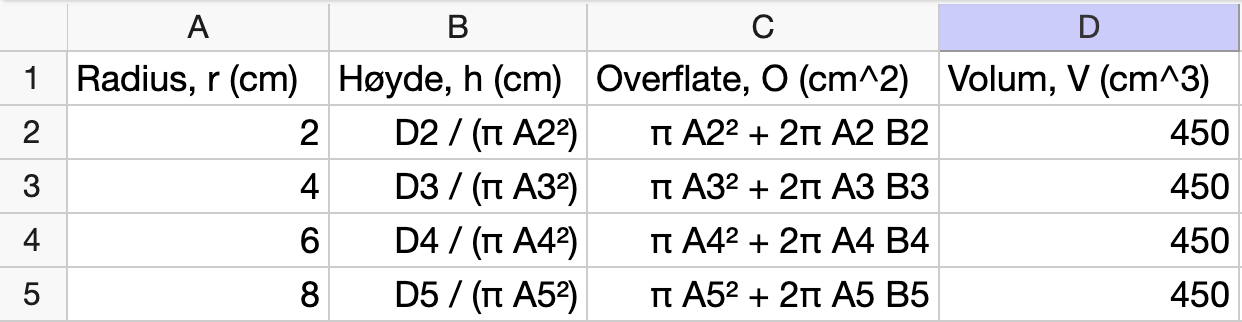
Vi kan skrive om formelen for volum slik at vi kan bestemme høyden \(h\) gitt et volum \(V\) og en radius \(r\) som:

\[ V = \pi \cdot r^2 \cdot h \liff h = \dfrac{V}{\pi \cdot r^2} \]

Deretter lager vi et regneark der vi fyller ut tabellen:

Nedenfor vises en oversikt over formlene som er brukt i regnearket:

b

Sett opp et funksjonsuttrykk Isabel kan bruke, og lag en grafisk framstilling som viser sammenhengen mellom radius og overflate.

Løsning

Vi kan lage et funksjonsuttrykk \(O(r)\) for overflaten \(O\) av boksen for en gitt høyde \(r\). Volumet \(V = 450\), så vi kan sette opp et likningssystem for å bestemme \(O(r)\). Vi løser likningssystemet med CAS:

som betyr at vi kan skrive

\[ O(r) = \dfrac{\pi r^3 + 900}{r} \and h = \dfrac{450}{\pi r^2}. \]

Deretter kan vi lage en grafisk framstilling av funksjonen \(O(r)\):

c

Hvor står må radius i boksene være for at overflaten skal bli minst mulig?
Hvor stor blir overflaten da?

Løsning

For å bestemme hvilken radius som gir minst mulig overflate, så kan vi løse likningen

\[ O'(r) = 0 \]

Deretter kan vi regne ut \(O(r)\) i dette punktet. Vi gjør dette med CAS:

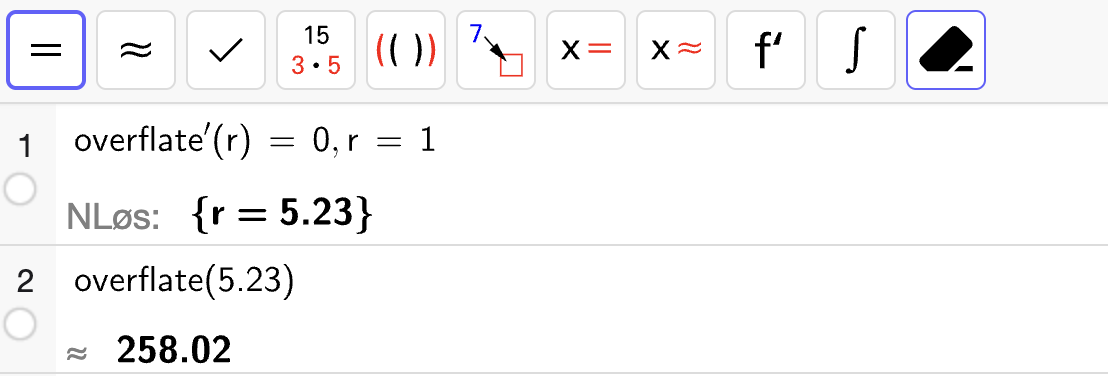
Ut ifra den grafiske framstillingen fra b kan vi være sikre på at løsningen her gir et bunnpunkt og dermed den minste overflaten. Vi har da at boksen har minst overflate dersom

\[ r \approx 5.23 \, \mathrm{cm} \]

som gir en overflate på ca. \(258 \, \mathrm{cm}^2\).