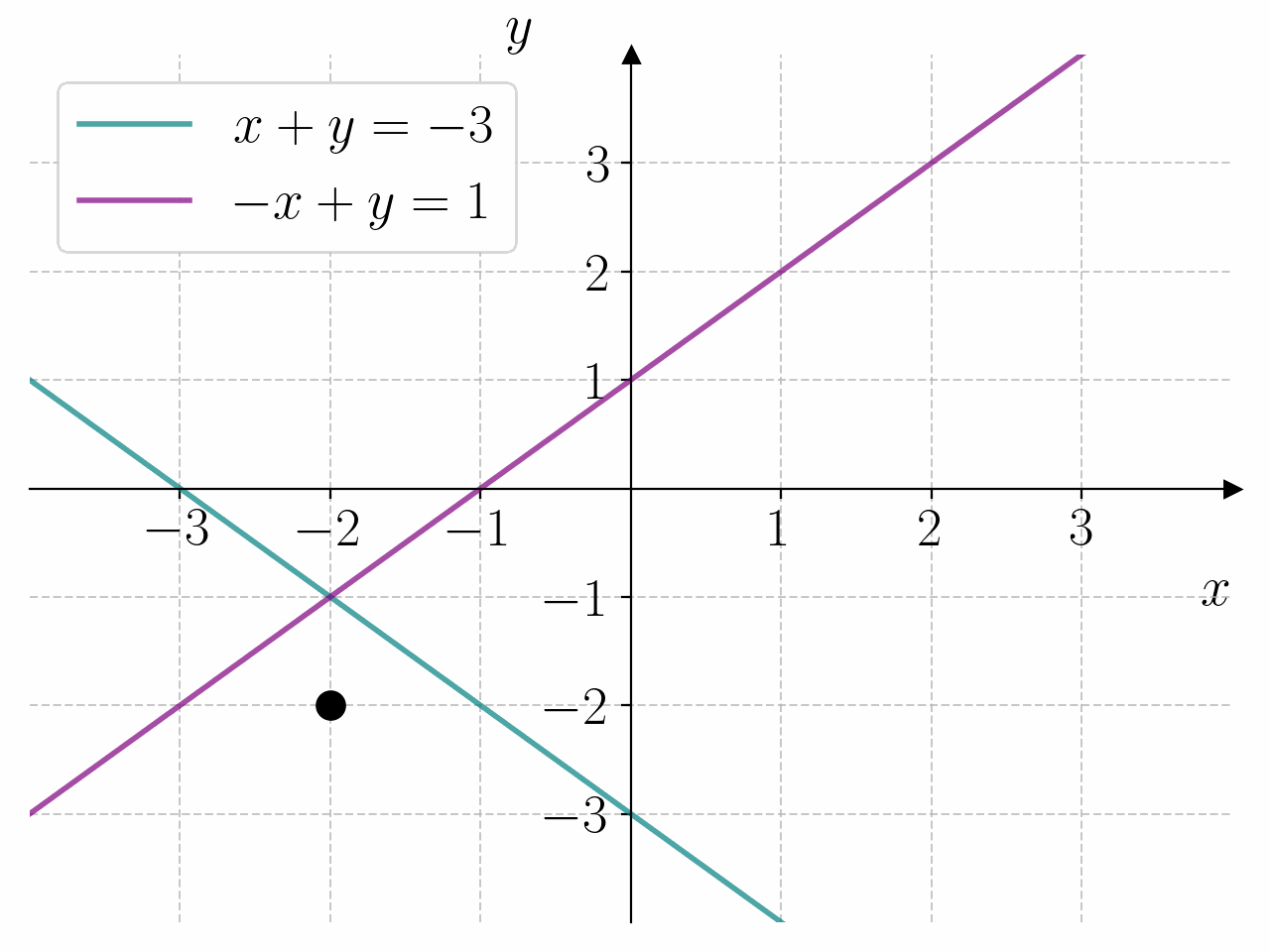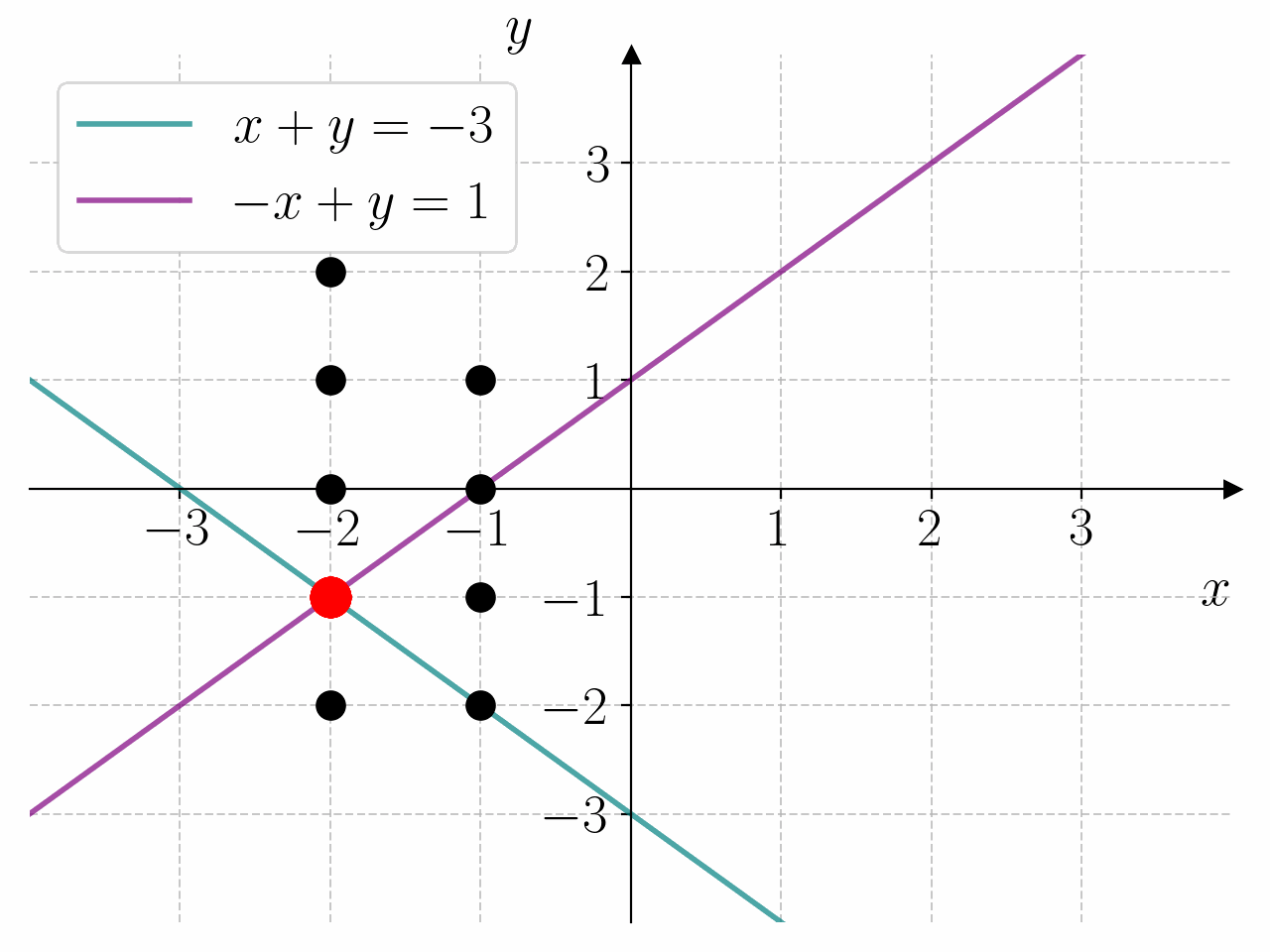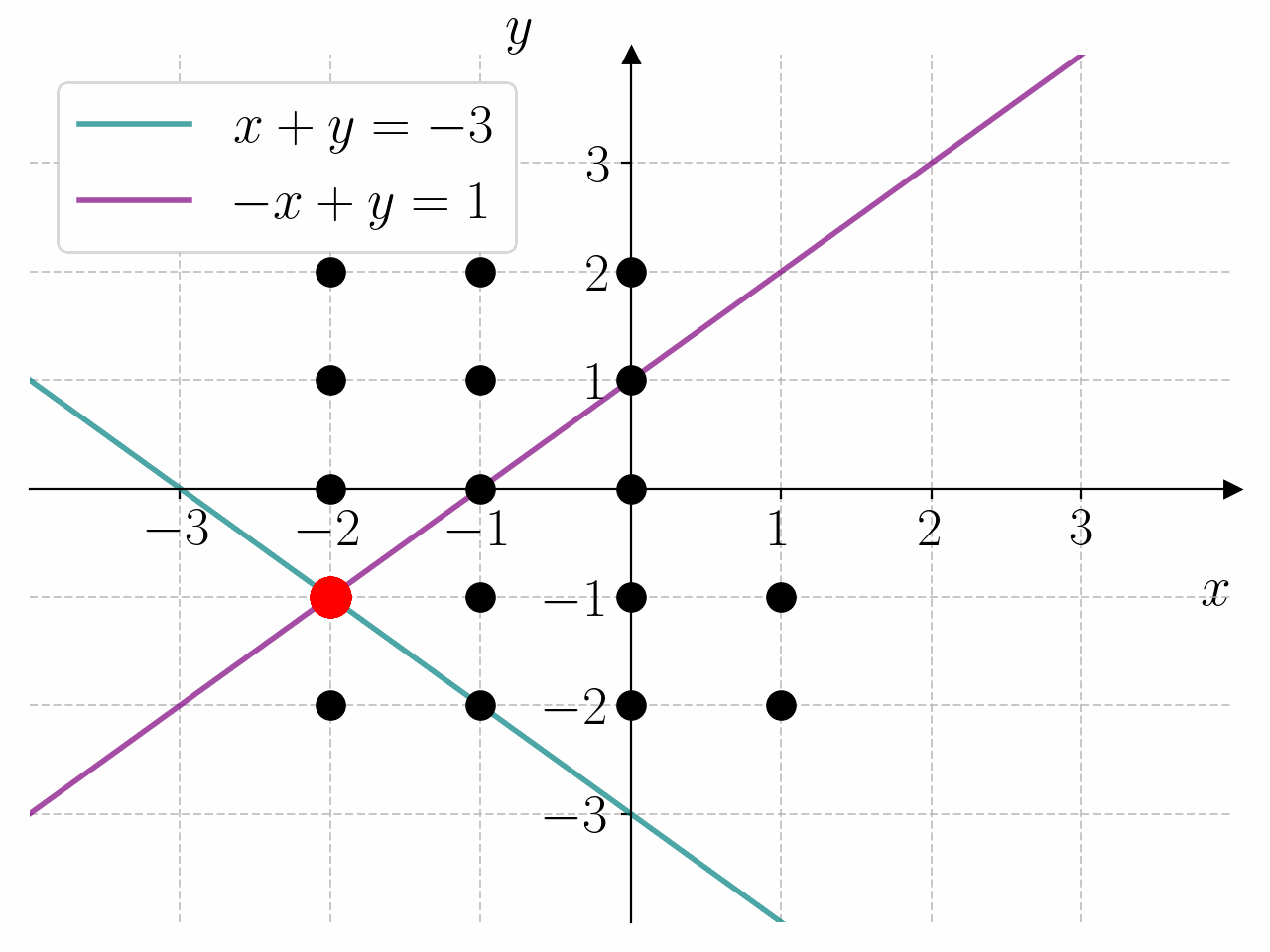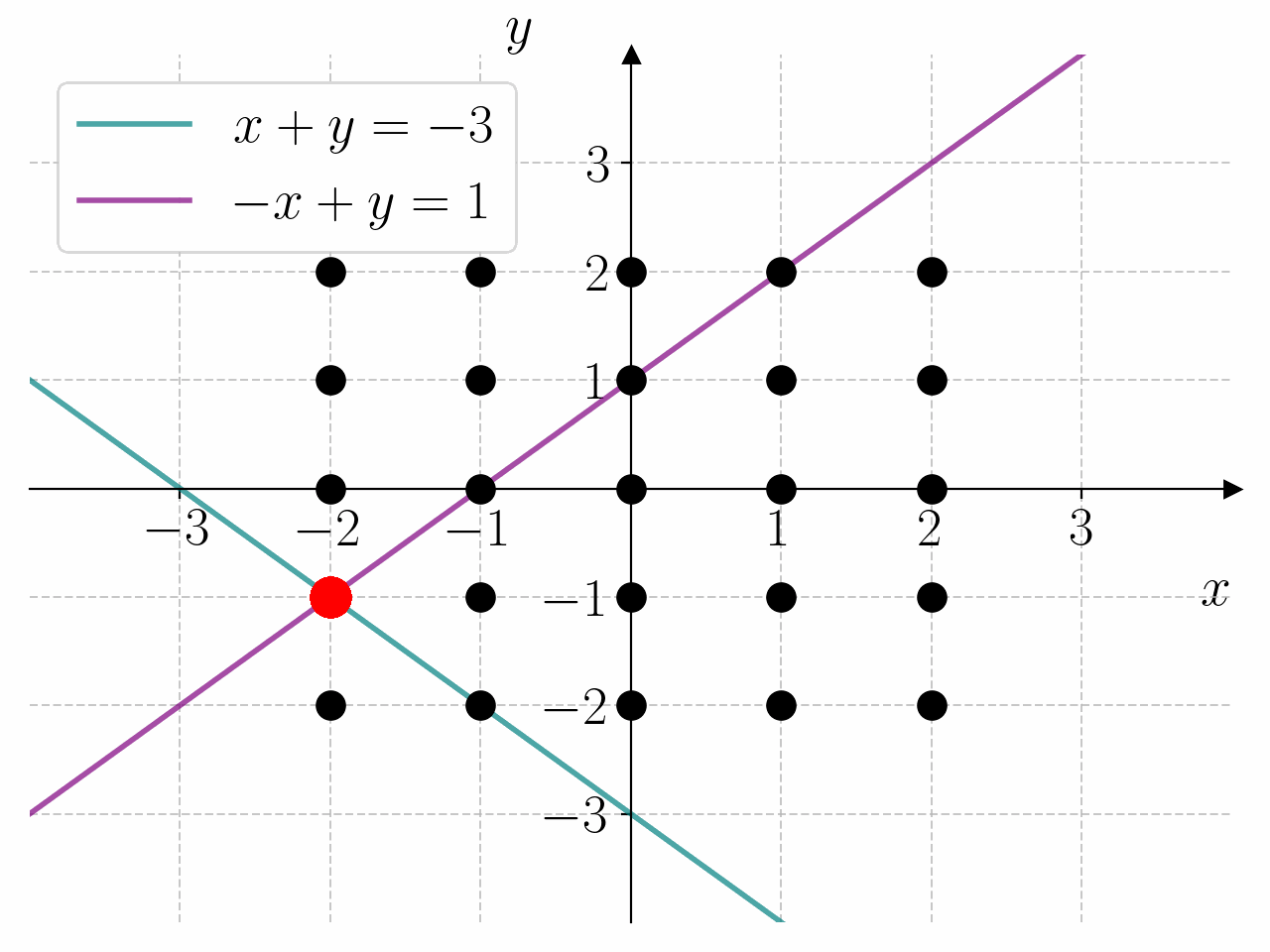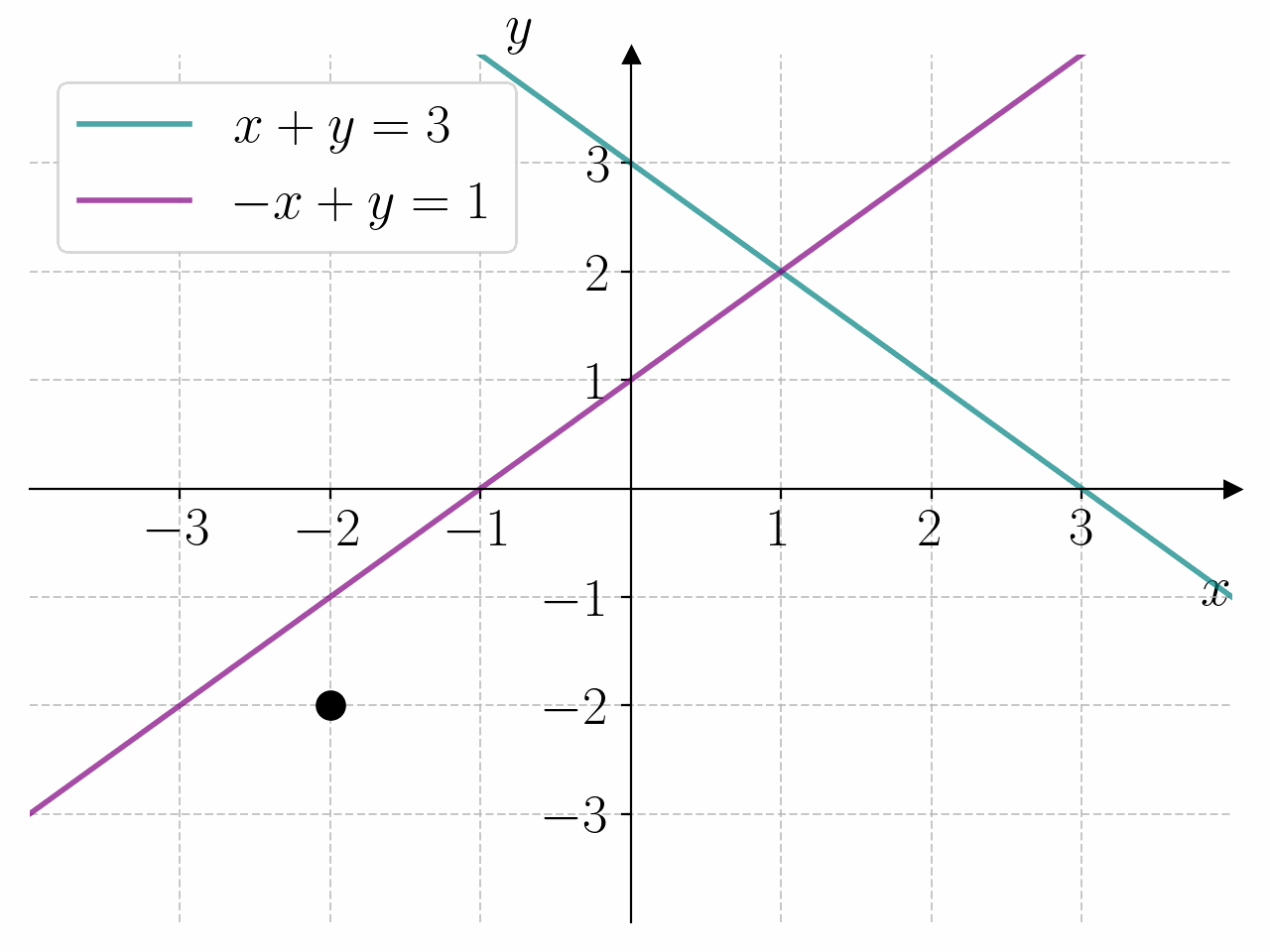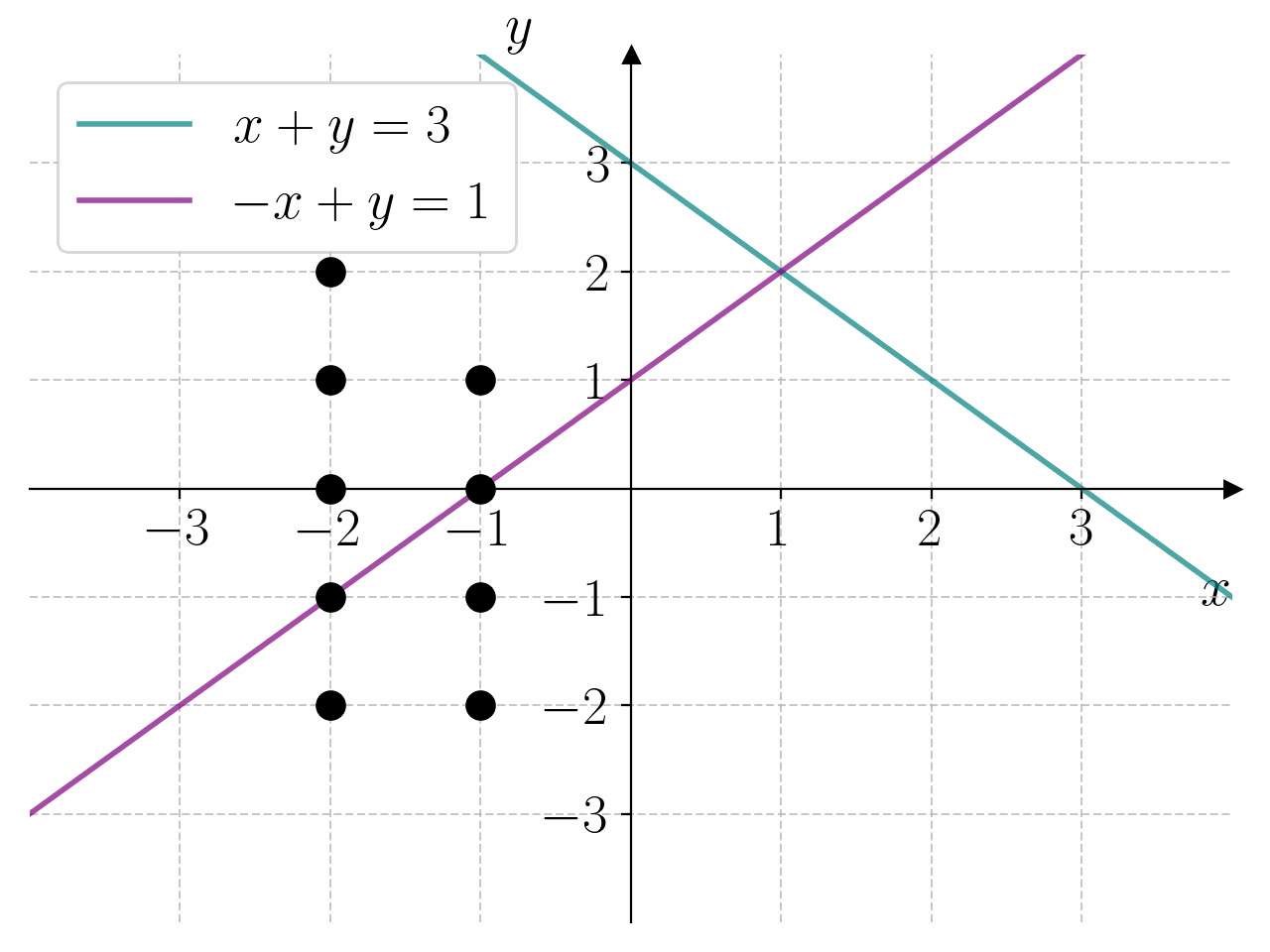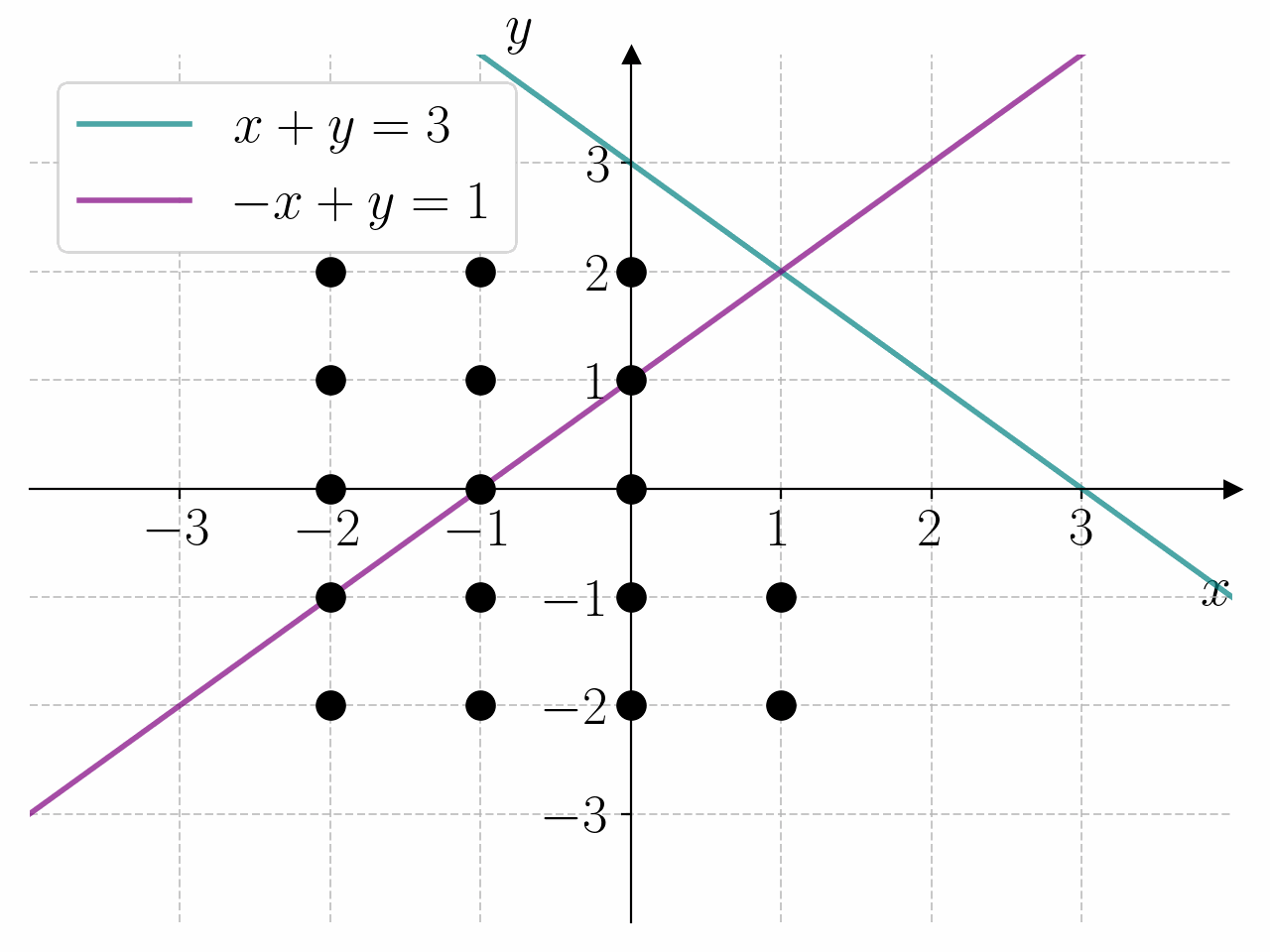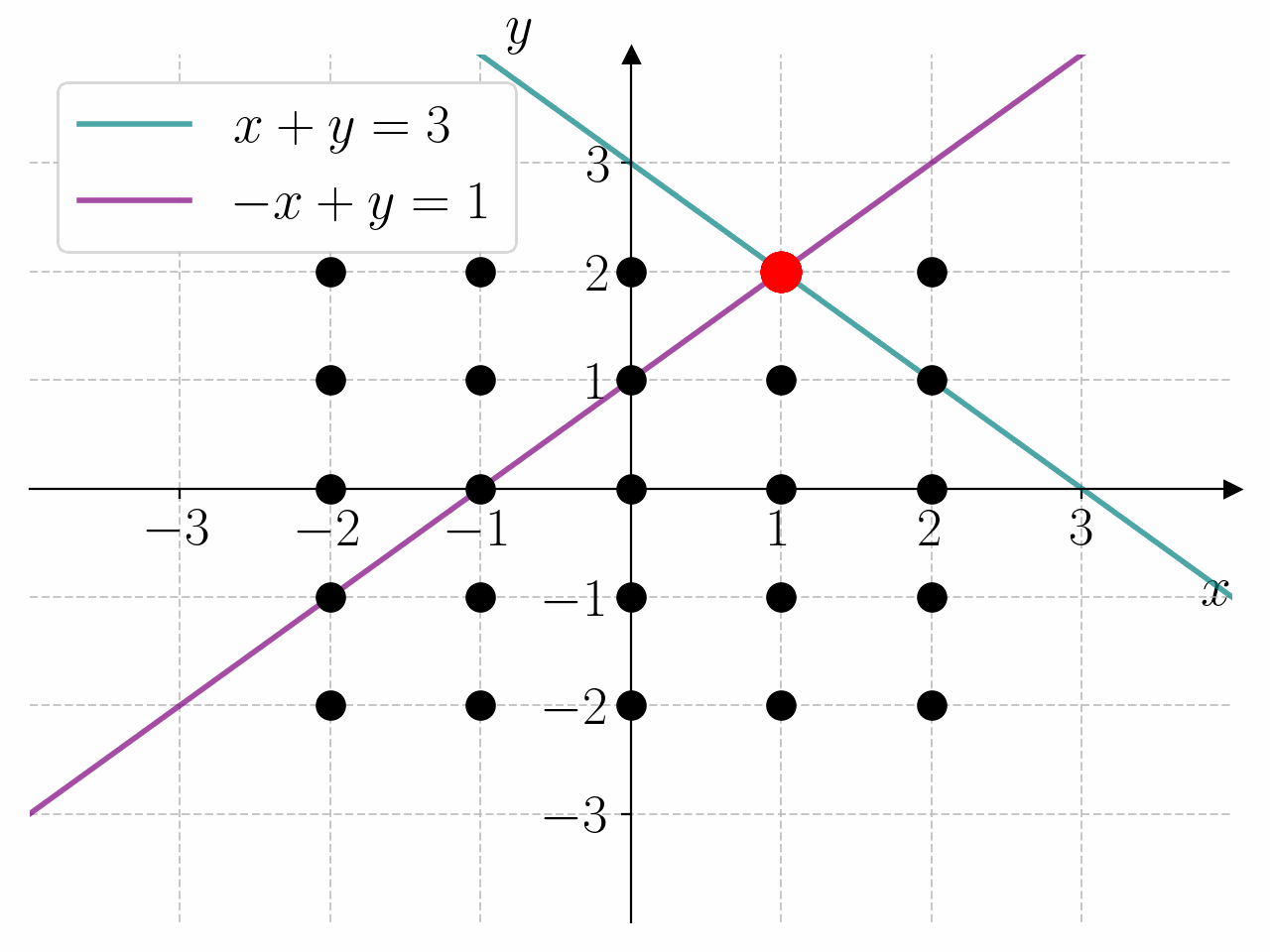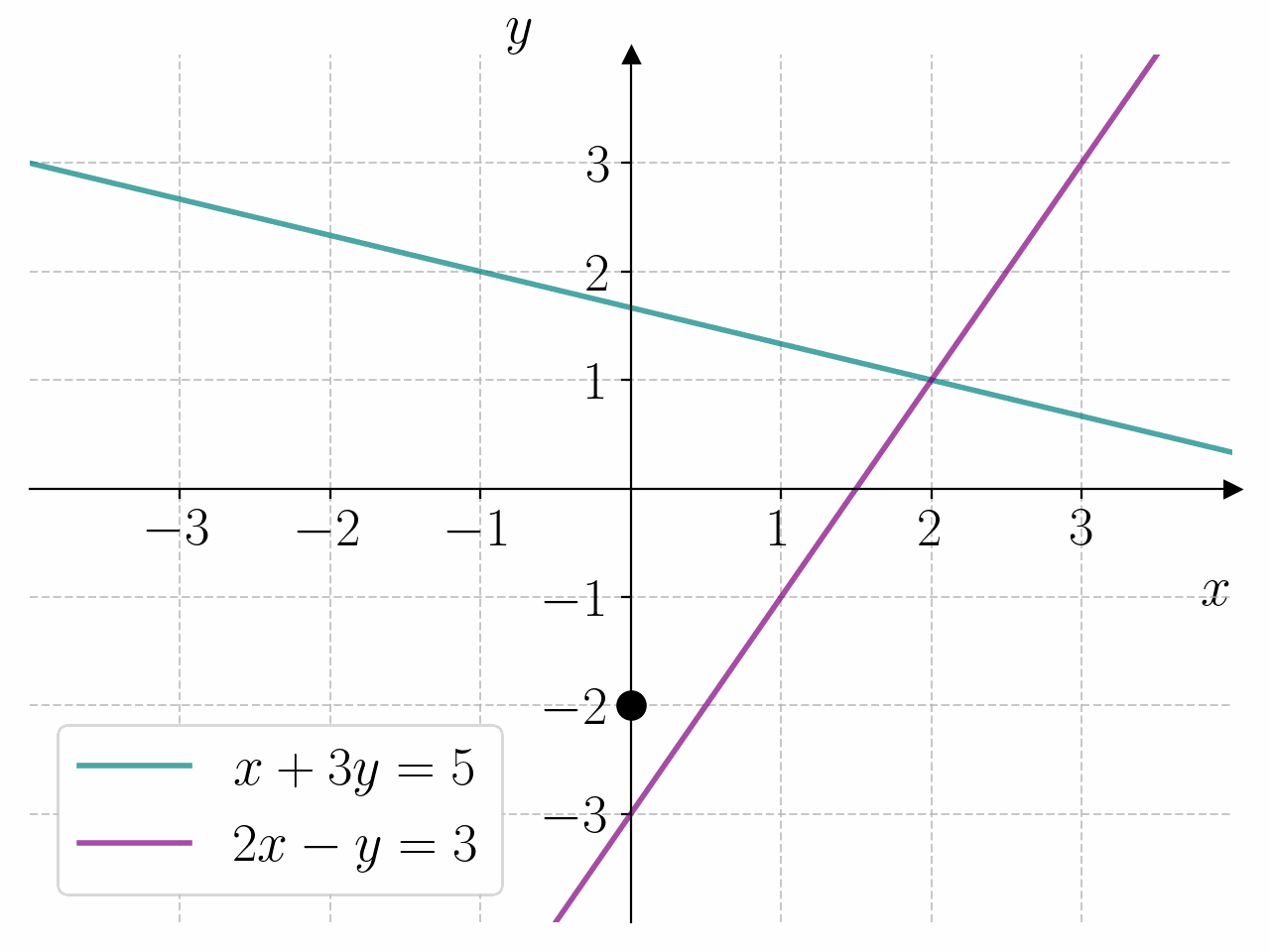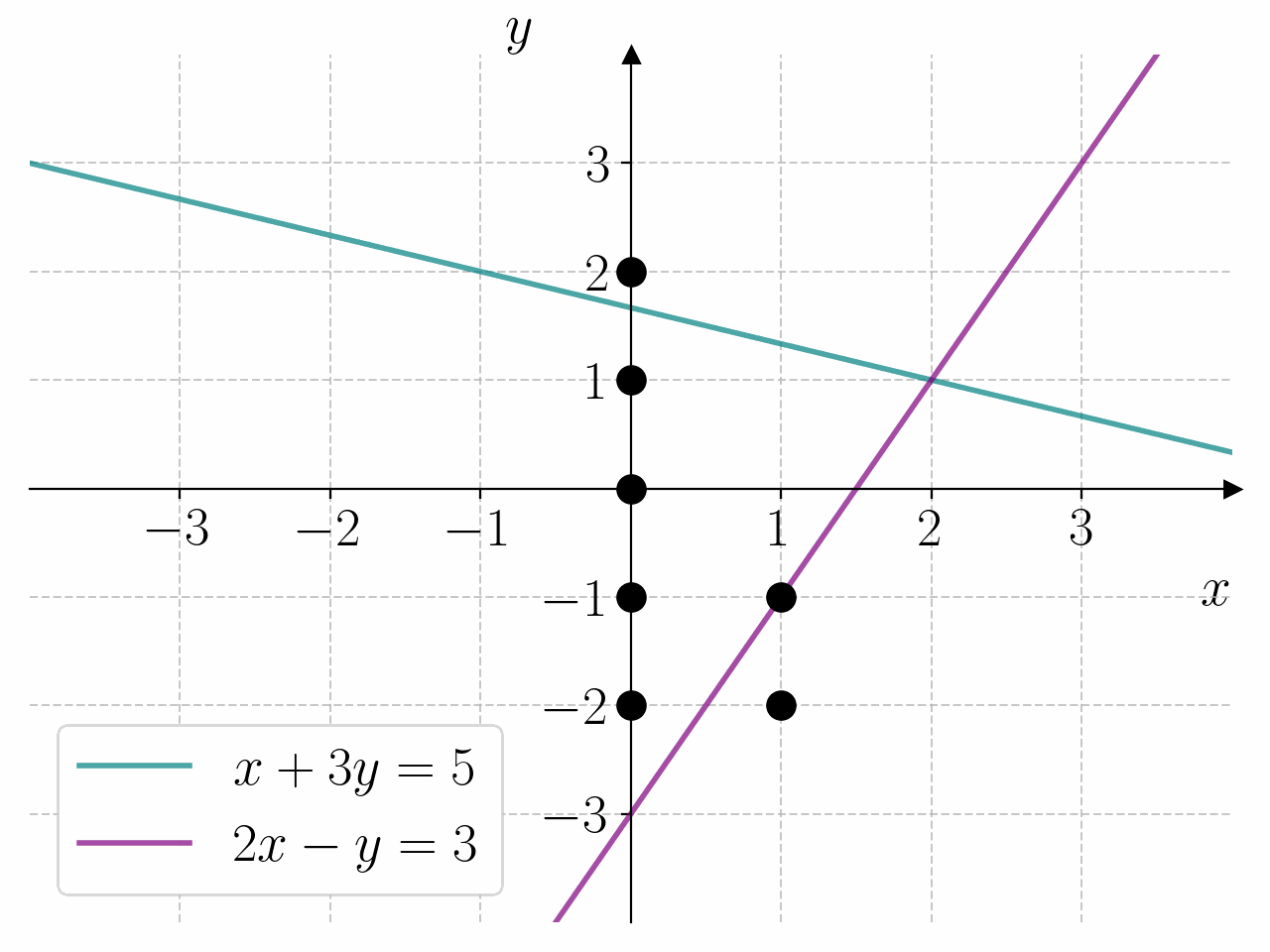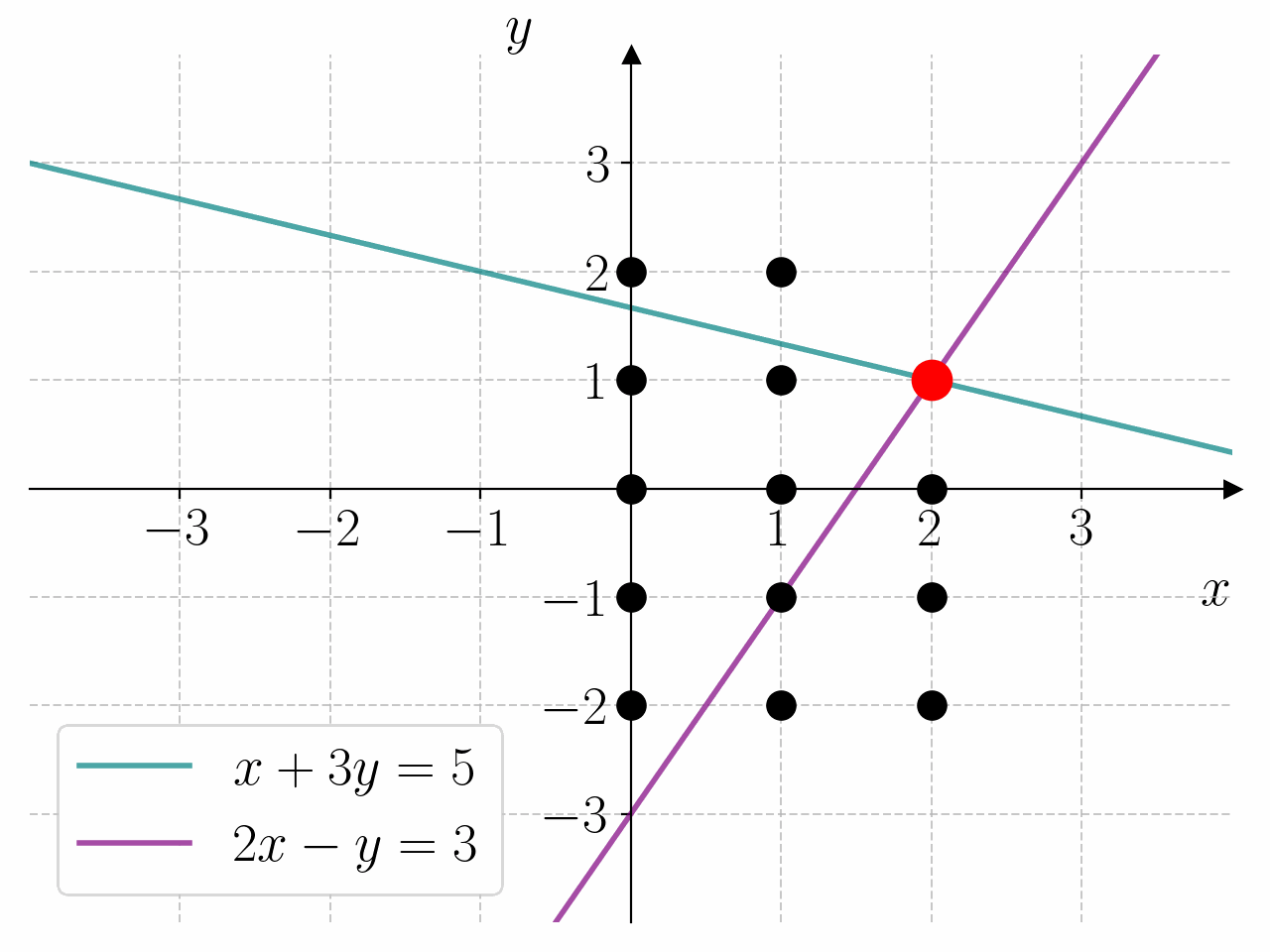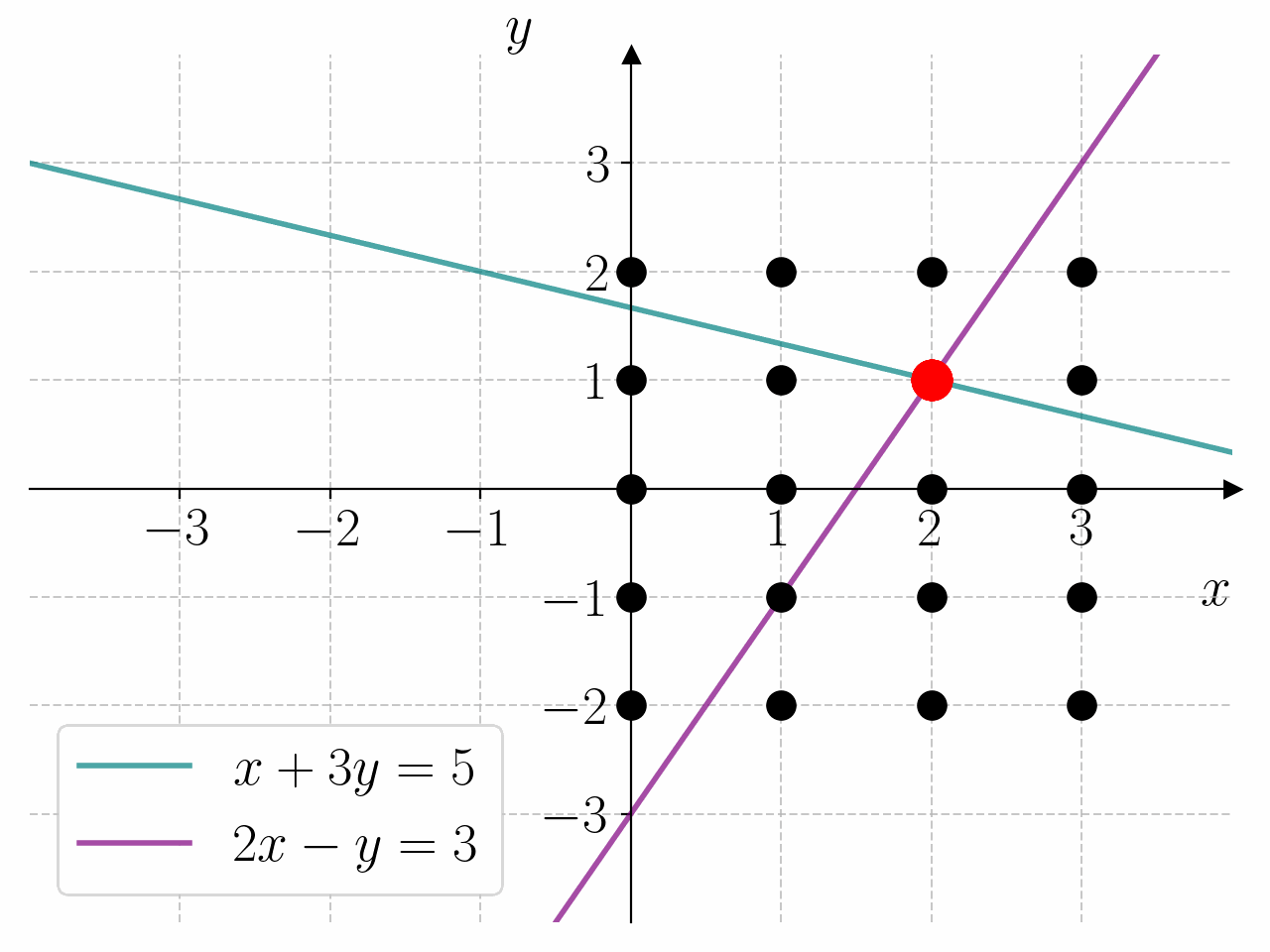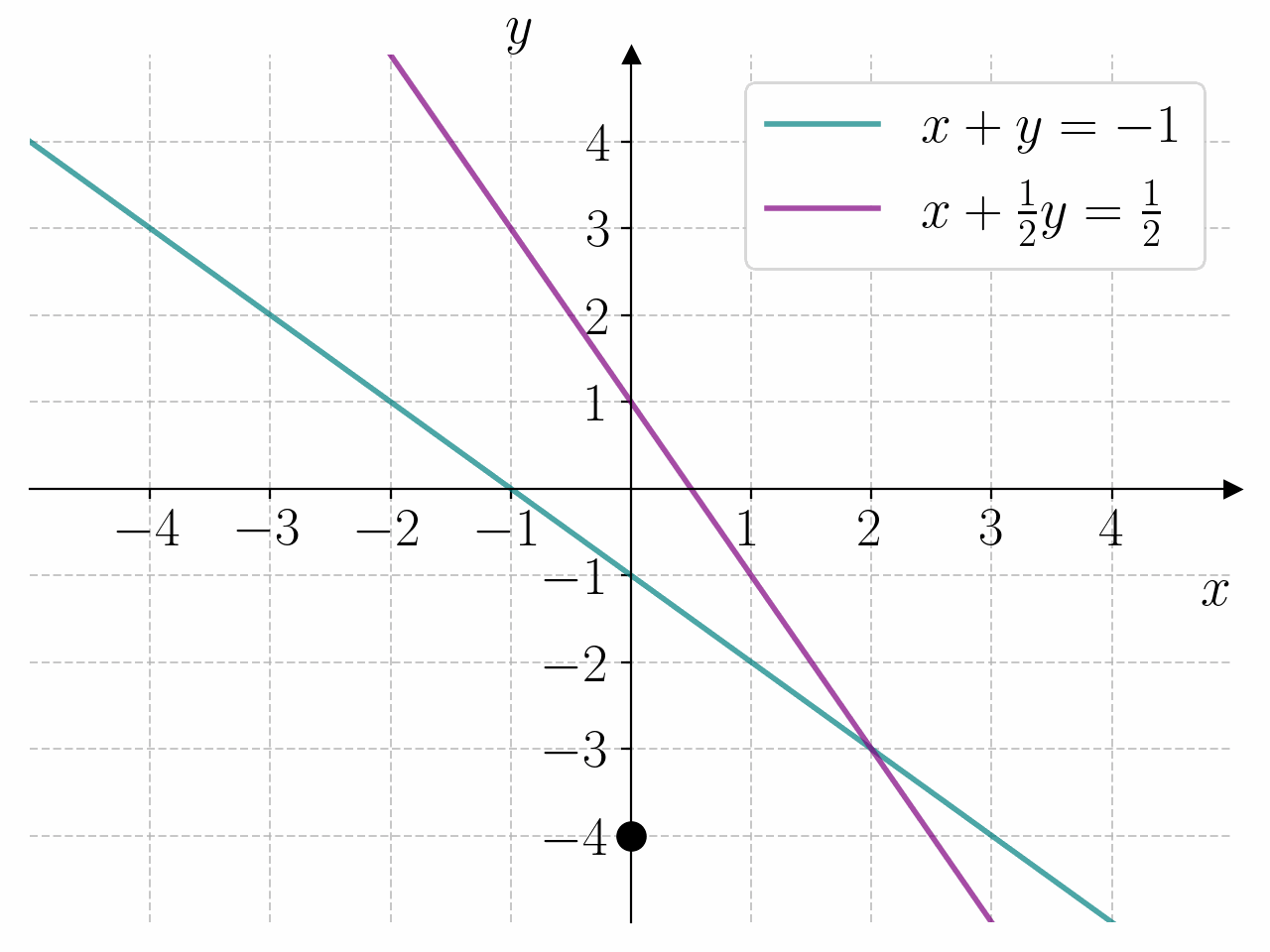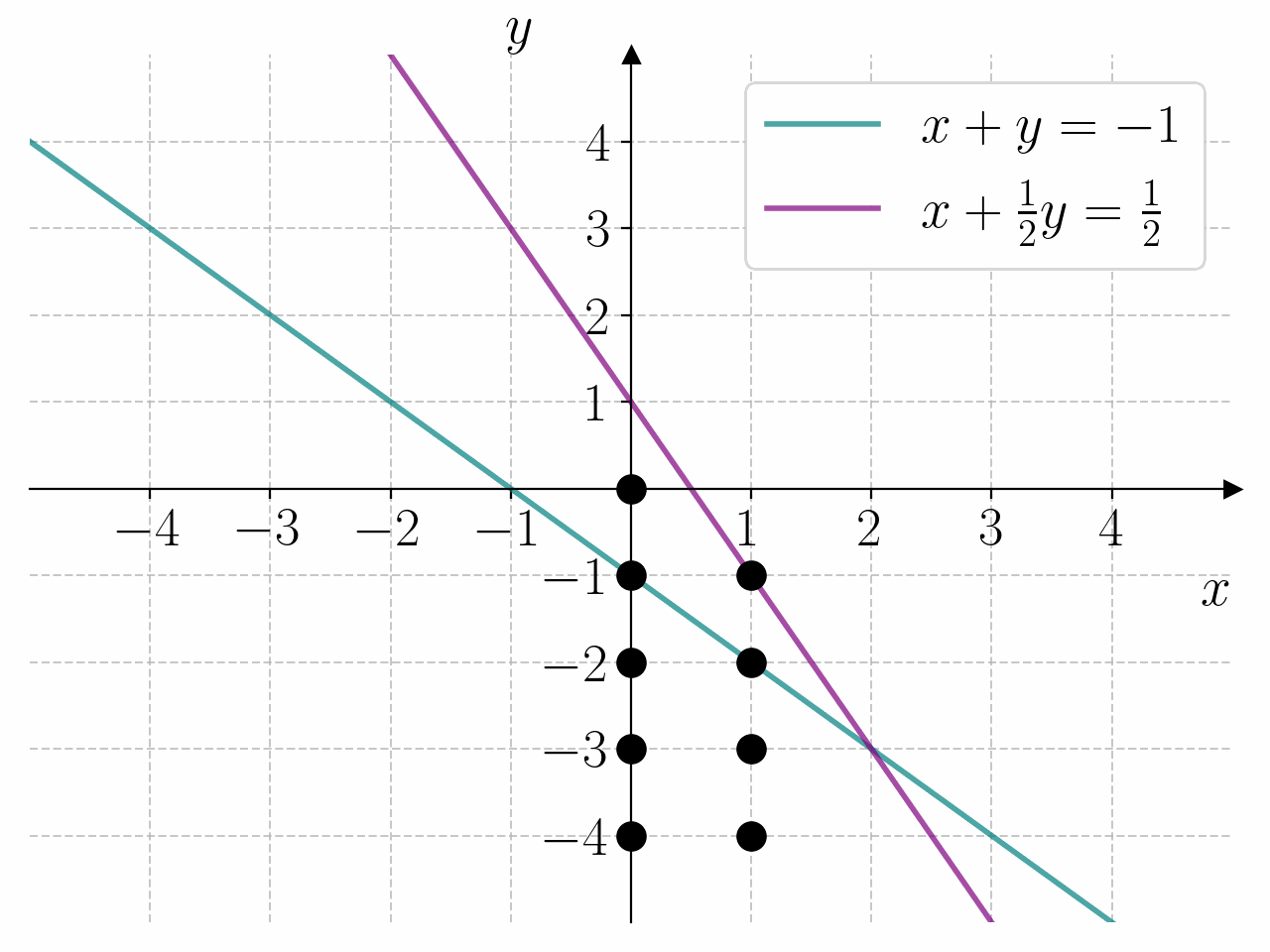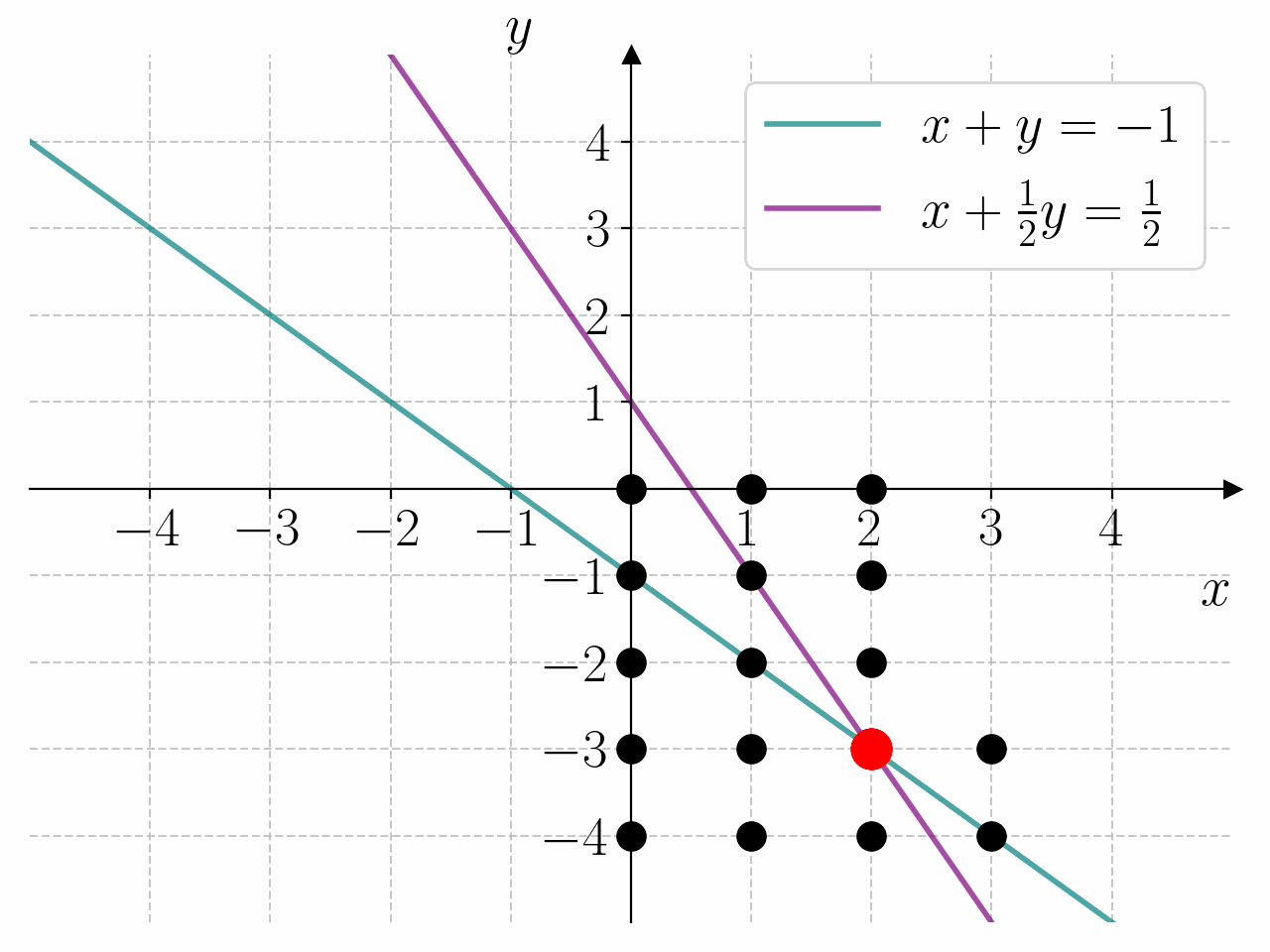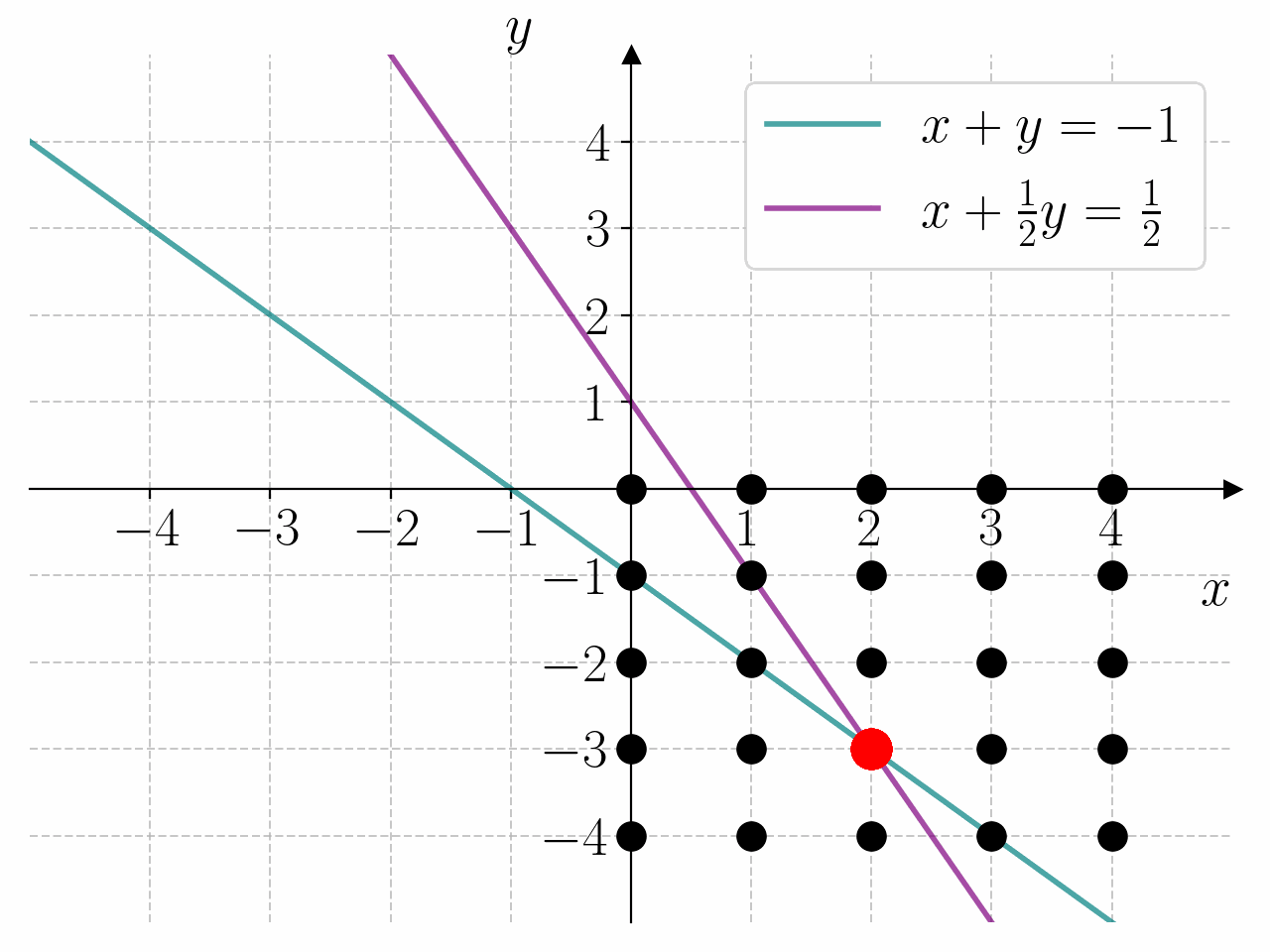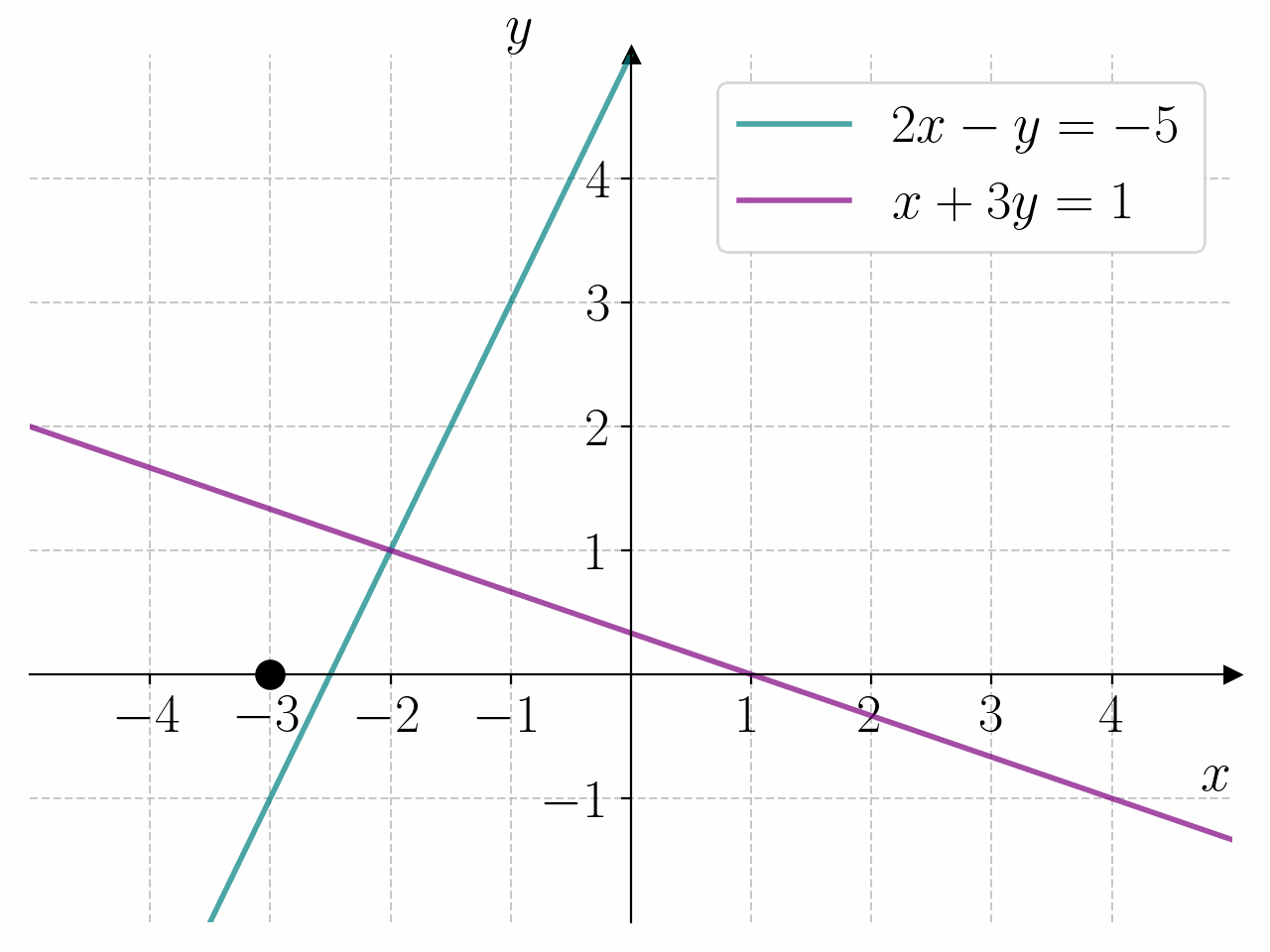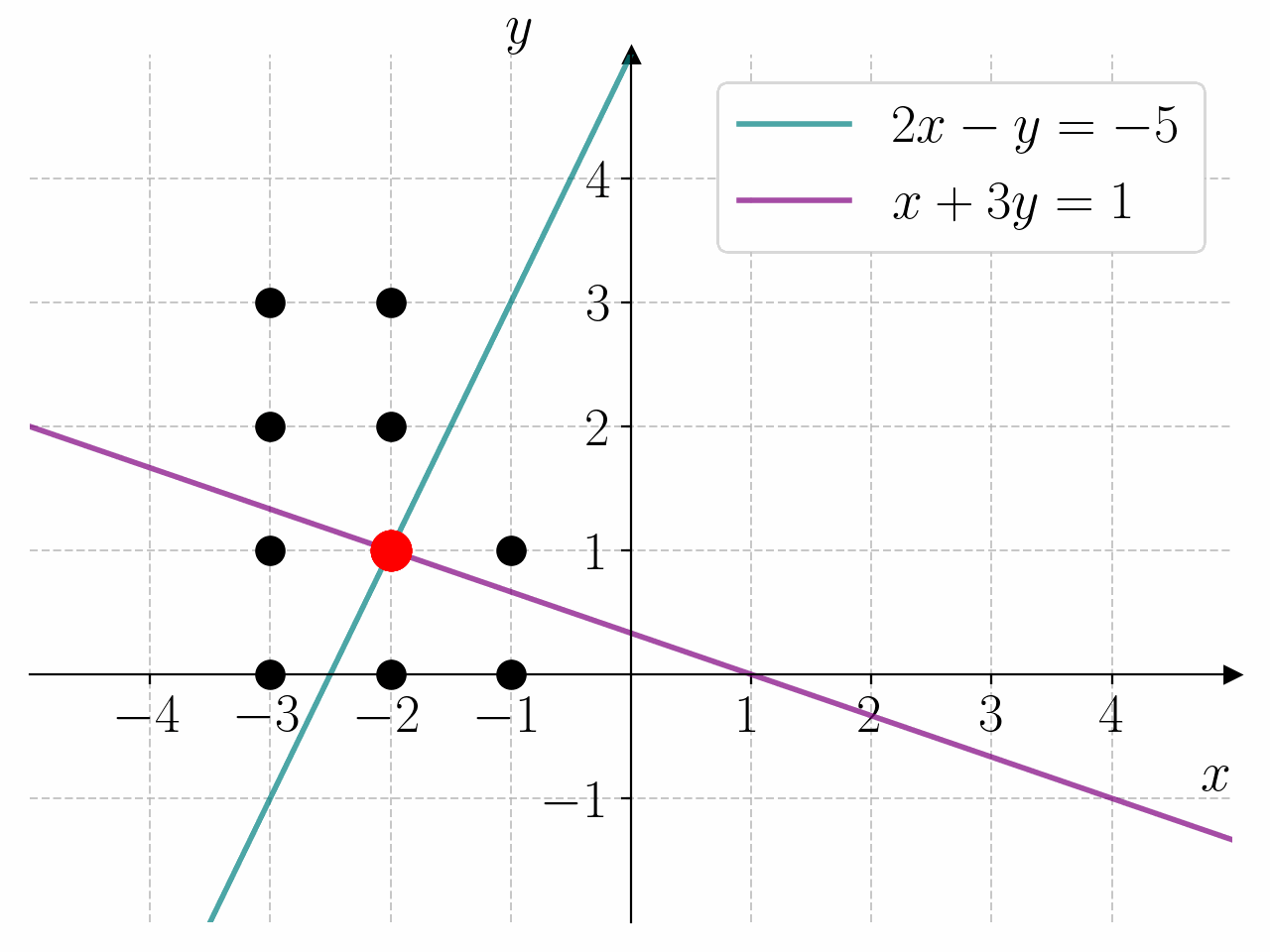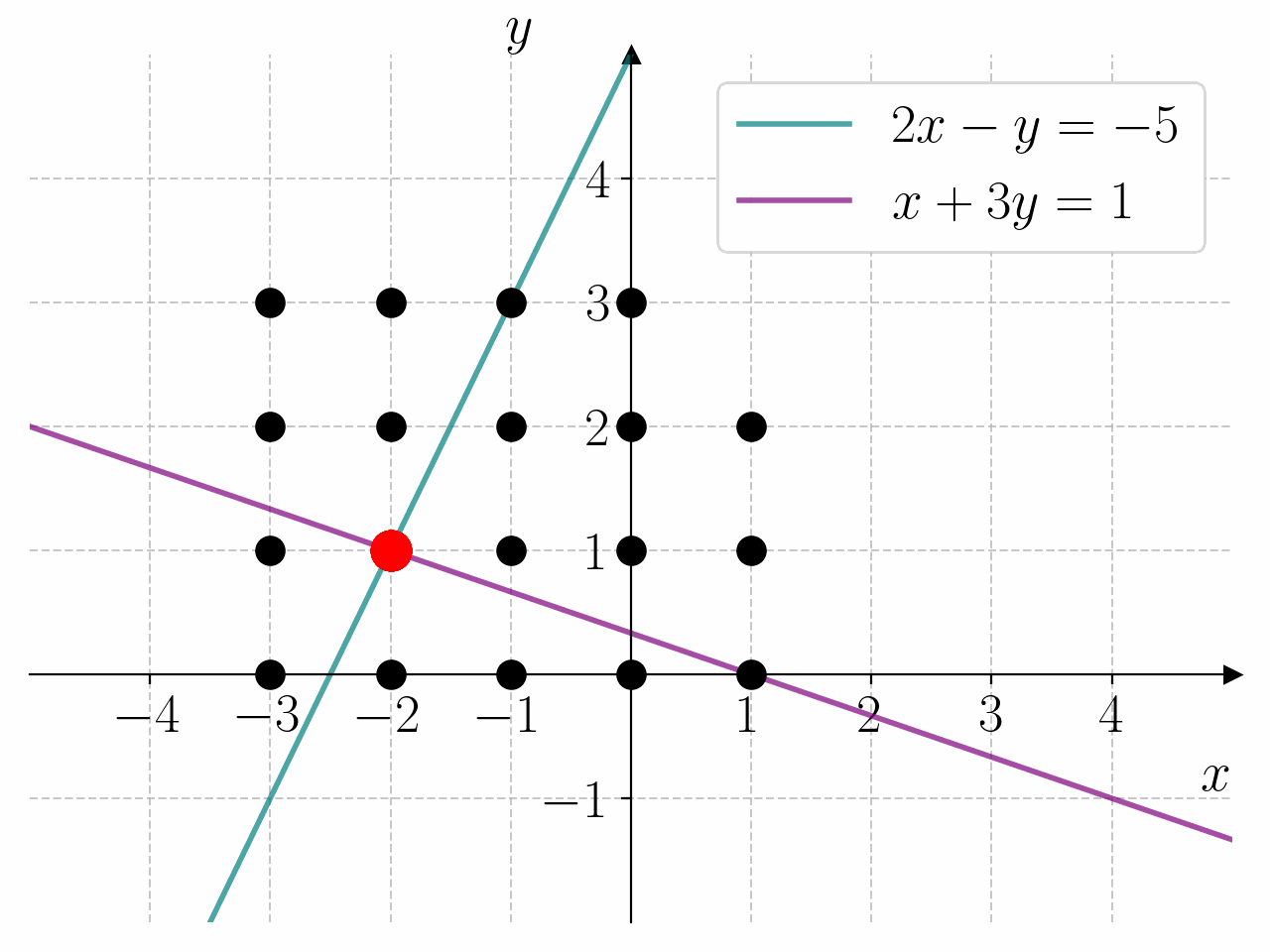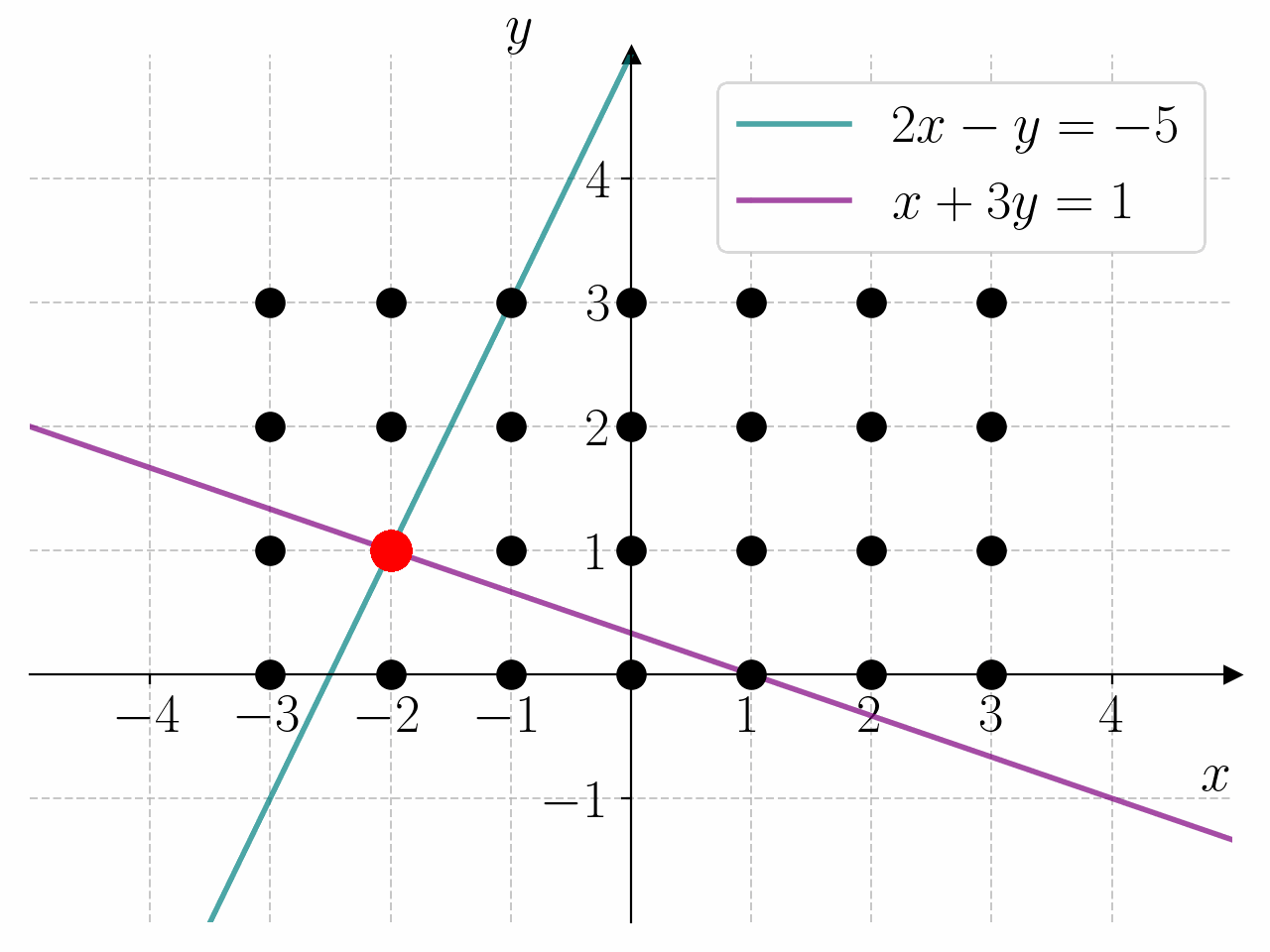Programmering av likningssystemer

5.3. Programmering av likningssystemer#

Læringsmål

Målet etter dette delkapittelet er at du skal:

  • Kunne lese, tolke og endre på programkode som løser lineære likningssystemer.

  • Kunne lese, tolke og lage nøstede for-løkker for å lage punkter i et rutenett og bruke dette til å løse likningssystemer.

Numerisk løsning av likningssystemer#

Akkurat som at det finnes likninger som ikke har noen analytisk løsning, finnes det også likningssystemer der dette er tilfellet. I andre tilfeller vil vi ha likningssystemer med så mange likninger og variabler at å løse dem uten datamaskin er en håpløs oppgave.

Her skal vi se på hvordan vi kan bruke programmering til å finne løsninger til lineære likningssystemer.

Repetisjon#

Først bør vi starte med å få repetert det viktigste vi trenger for å løse likningssystemer med programmering.

Repetisjon 1:

Her kommer en quiz om for-løkker, funksjoner i Python og løsning av likninger med programmering.

Ta quizen!

Svar på så mange spørsmål du kan før tiden er ute! ⏳

Løsning av likningssystemer med programmering#

Utforsk 1: strategi 1

I mange tilfeller kan vi skrive om et likningssystem fra dens generelle form til en form som svarer til to lineære funksjoner. Da kan vi tolke likningssystemet som at vi skal bestemme koordinatene til skjæringspunktet \((x, y)\) mellom grafene til de to funksjonene.

Eksempel

\[ 5x + y = 2 \quad \land \quad 3x - y = 2 \]

kan skrives om ved å løse begge likninger for \(y\) til:

\[ y = \underbrace{-5x + 2}_{\displaystyle f(x)} \quad \land \quad y = \underbrace{3x - 2}_{\displaystyle g(x)} \]

Løsningen av likningssystemet er da bare koordinatene til skjæringspunktet mellom grafene til \(f\) og \(g\).

Et likningssystem er gitt ved

\[ x + 2y = 5 \quad \land \quad 4x + y = 6 \]

Skriv om likningssystemet til formen

\[ y = ax + b \quad \land \quad y = cx + d \]

Hvilke to lineære funksjoner inngår i likningssystemet?

Fasit

\[ y = -\dfrac{1}{2}x + \dfrac{5}{2} \quad \land \quad y = -4x + 6 \]

Under vises et uferdig program som skal løse likningssystemet fra deloppgave a.

Fyll inn koden som mangler og kjør programmet for å bestemme løsningen av likningssystemet.

Sjekk svaret ved å sammenligne med figuren her når du er klar!

../../../../_images/utforsk_1.svg

Fig. 5.7 viser linjene i likningssystemet \(x + 2y = 5 \, \land \, 4x + y = 6\)#

Fasit

1def f(x):
2    return -x / 2 + 5 / 2
3
4def g(x):
5    return -4 * x + 6
6
7for x in range(-5, 6):
8    if f(x) == g(x):
9        print(x, f(x))

Utskriften blir

1 2.0

som betyr at løsningen av likningssystemet er

\[ x = 1 \, \land \, y = 2 \]

Utforsk 2

Her skal du utforske en strategi som vi kaller for gridsøk.

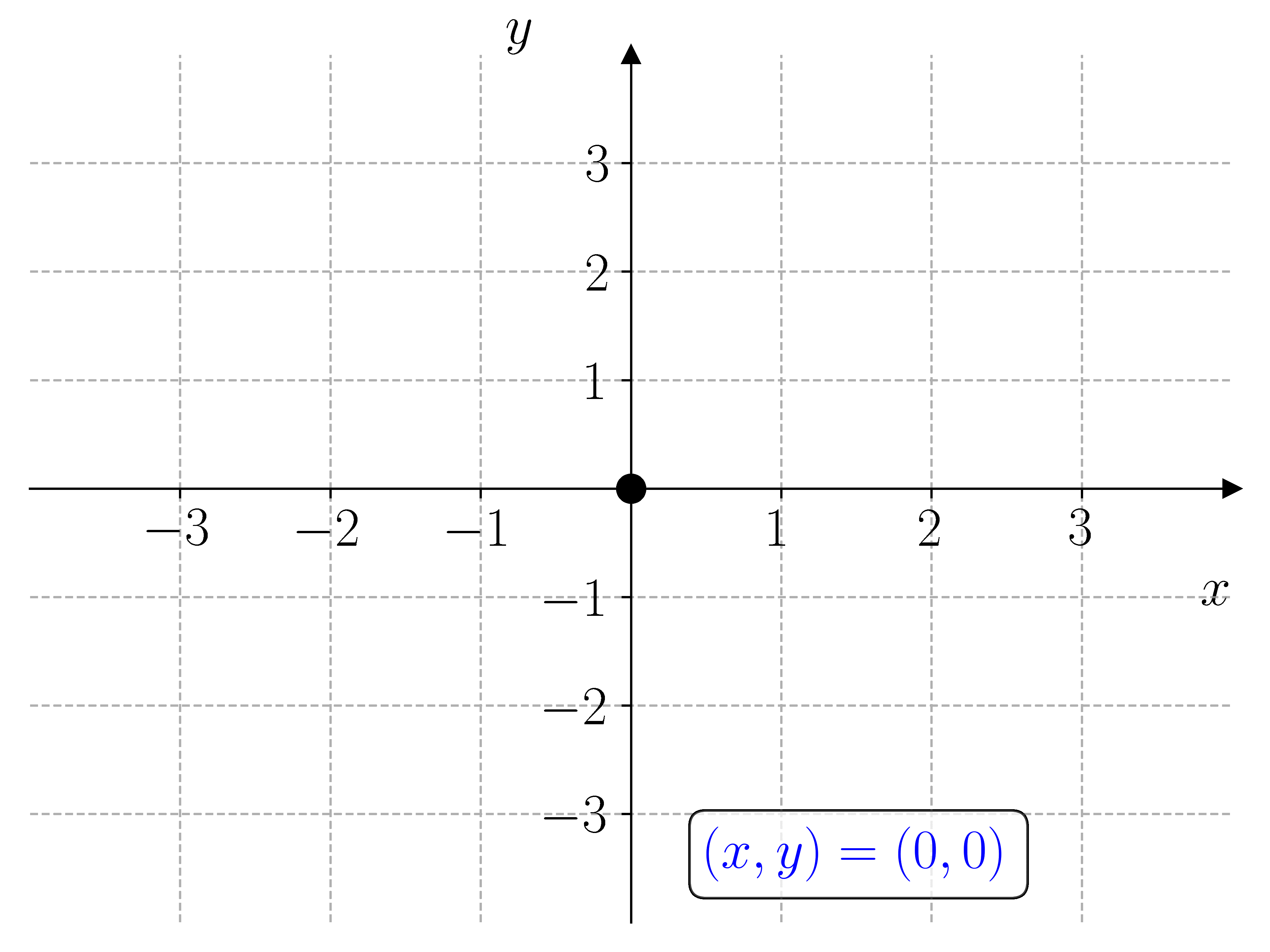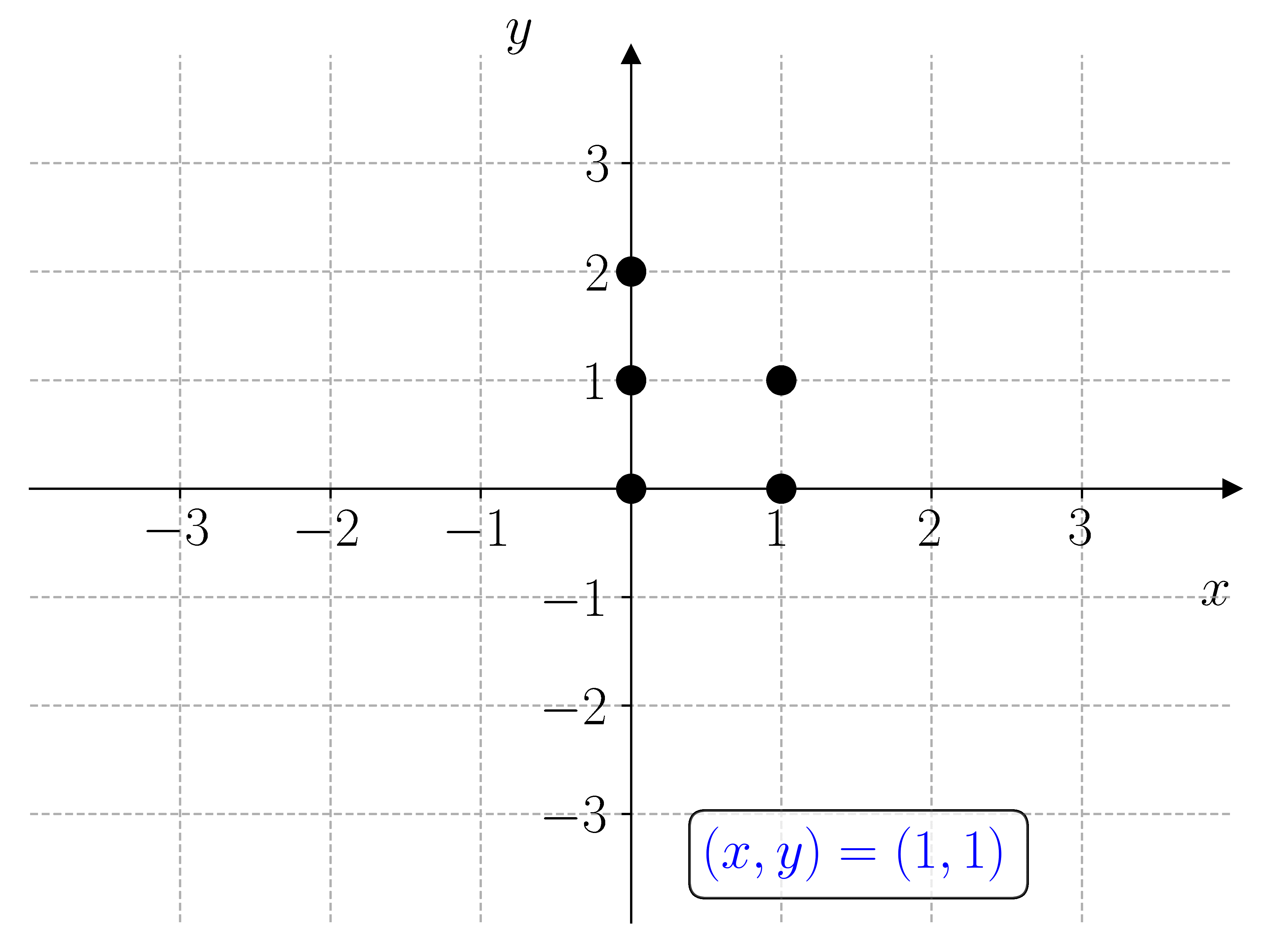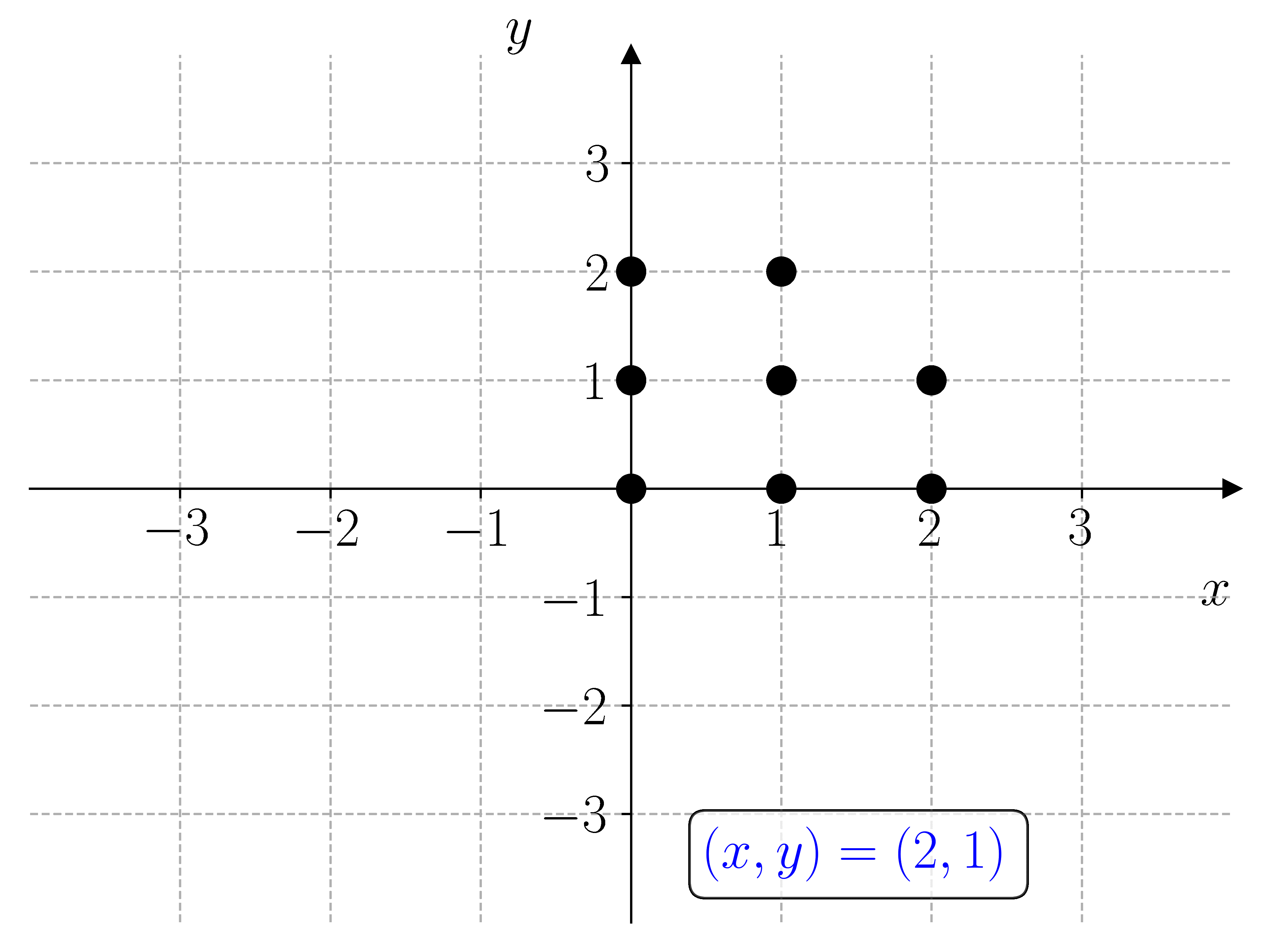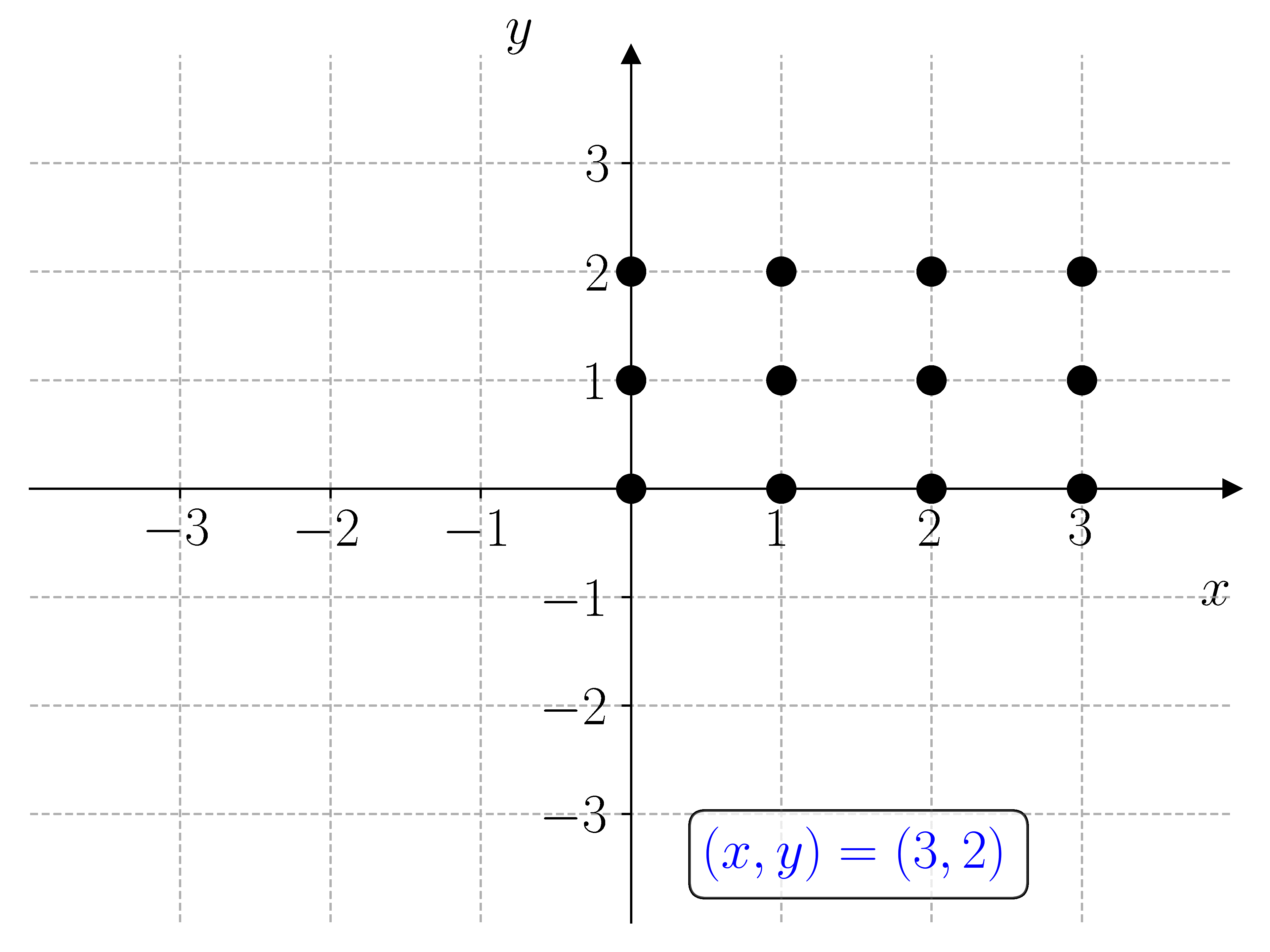
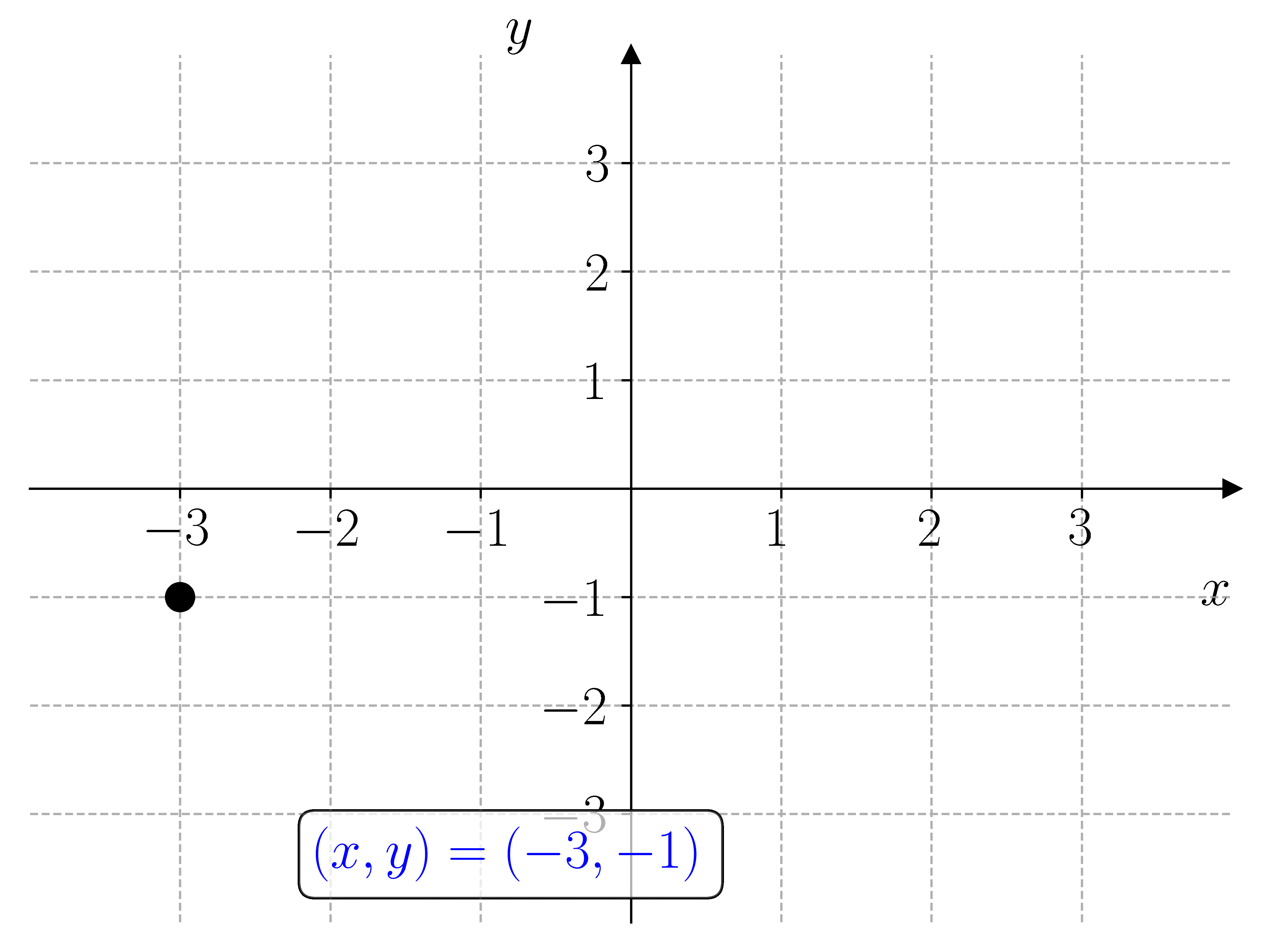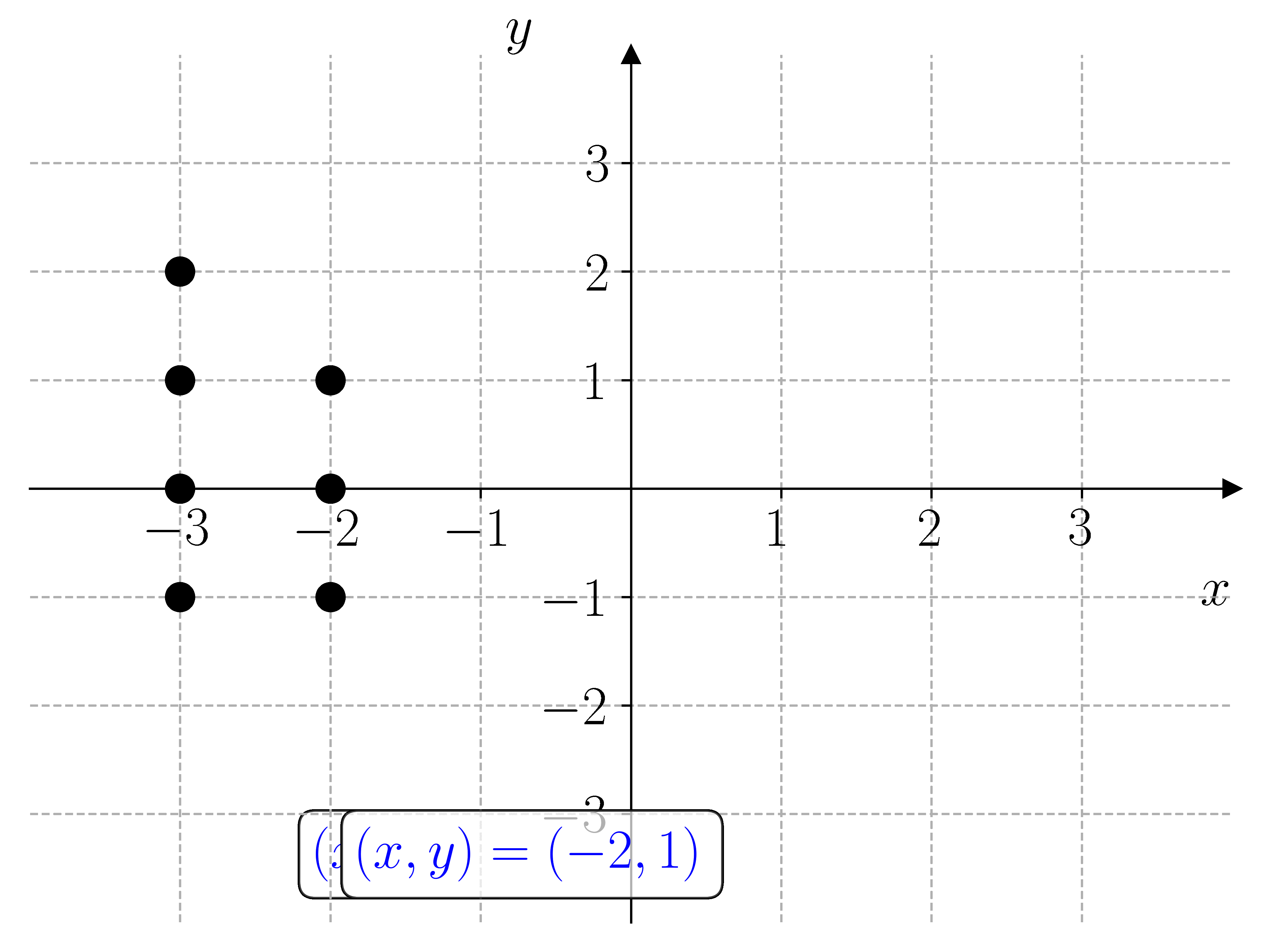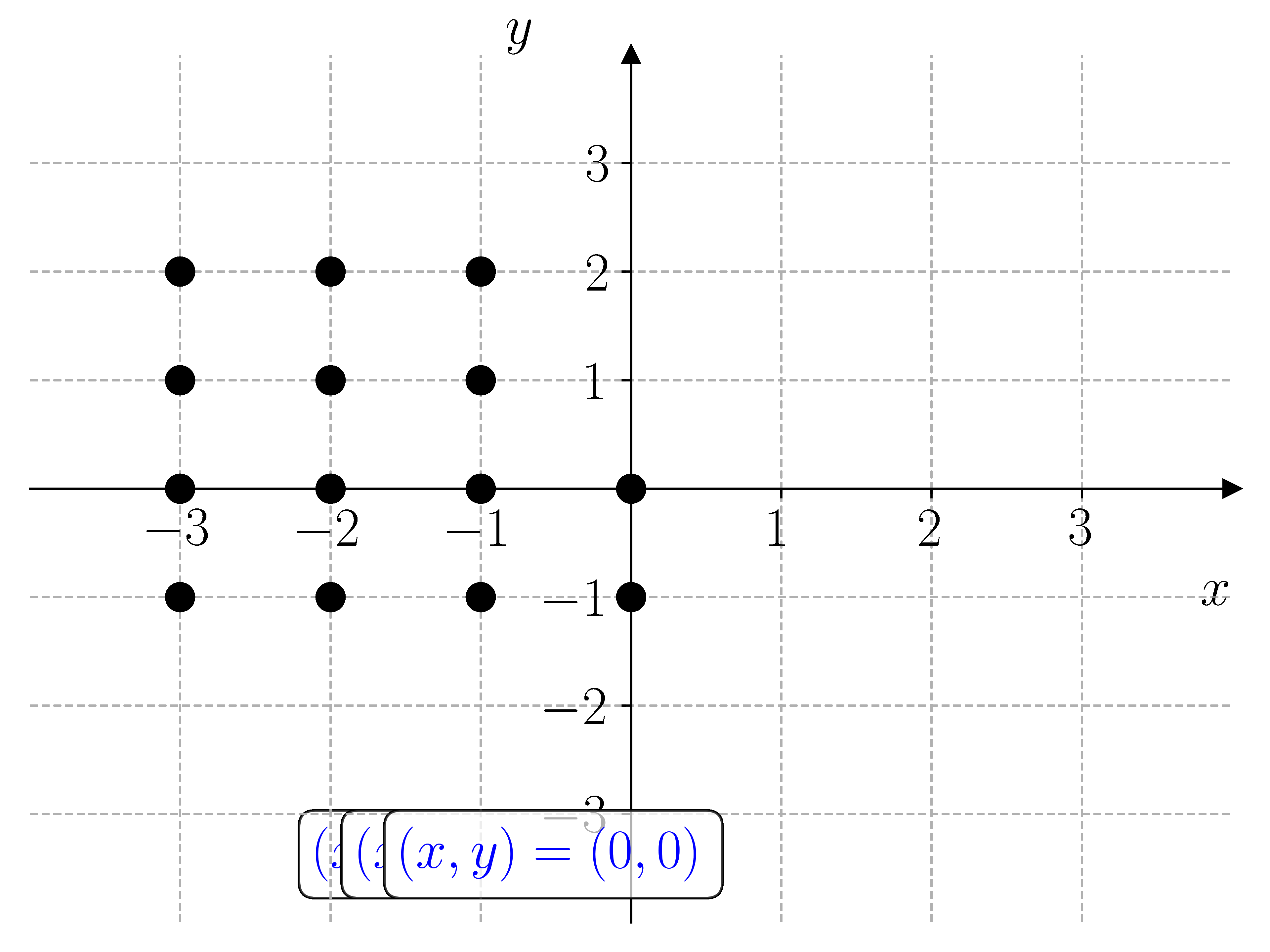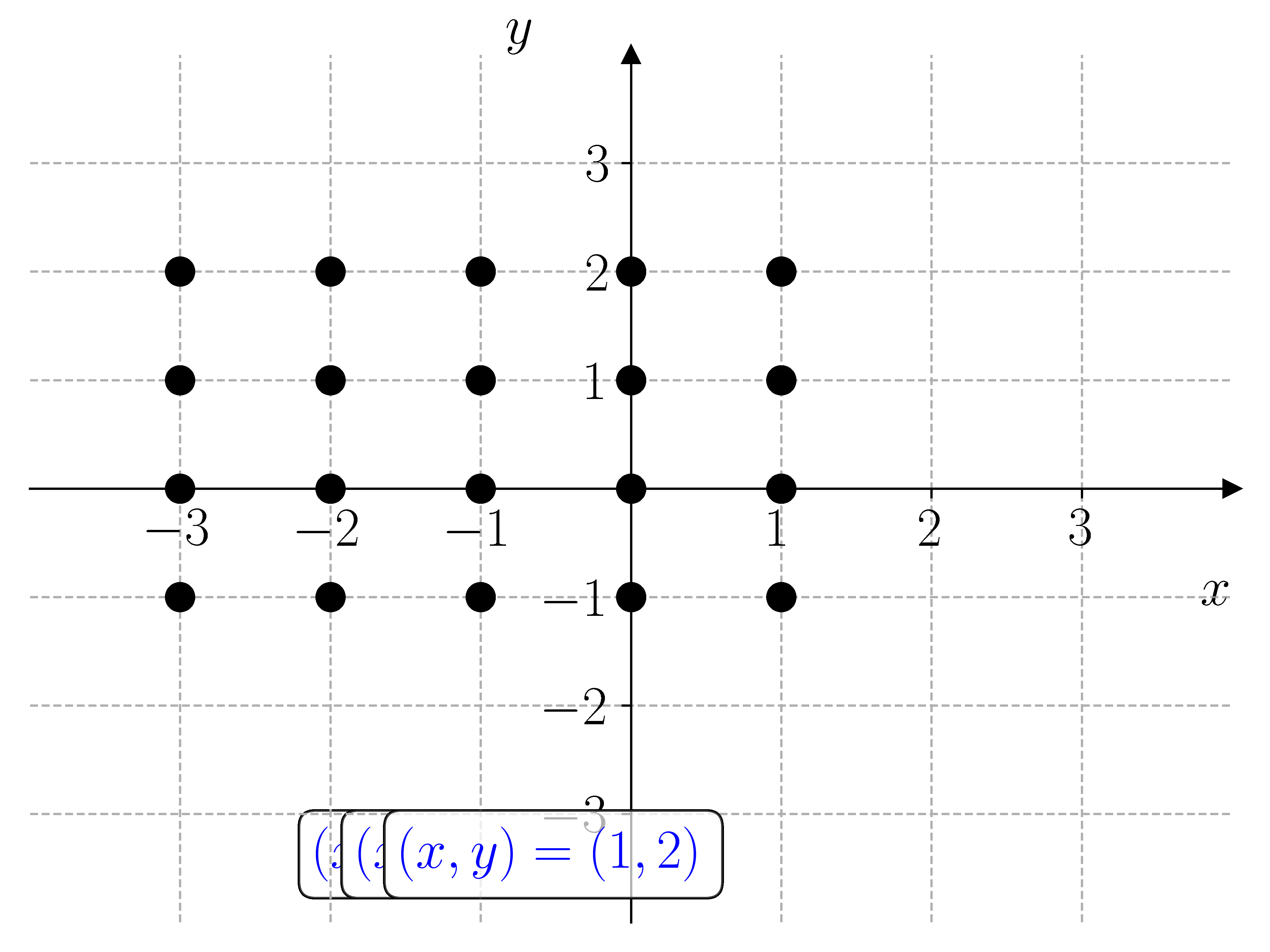
I prinsippet kan vi løse et hvert likningssystem ved å lage et rutenett med punkter \((x, y)\) i \(xy\)-planet og sjekke hvilke punkter som oppfyller likningssystemet. For å gjøre dette må vi lage nøstede for-løkker. Dette er for-løkker som ligger inne i hverandre. Den første for-løkken lager punktene \(x\), og den andre for-løkken lager punktene \(y\).

Nedenfor vises et program og en animasjon som henger sammen. Undersøk på hvilken måte.

Programkode

Animasjon

../../../../_images/animasjon.gif

Nedenfor vises et program og en animasjon som henger sammen. Undersøk på hvilken måte.

Programkode

Animasjon

../../../../_images/animasjon1.gif

Underveisoppgave 1

Ta quizen!

Utforsk 3: strategi 2

Her skal vi se hvordan vi kan bruke gridsøk til å finne løsningen av likningssystemer.

Vi trenger en måte å sjekke om et likningssystem er oppfylt for et punkt \((x, y)\). Med andre ord, vi må kunne sjekke om to likninger er sanne samtidig.

Under vises det tre eksemplekoder der man sjekker om et likningssystem er oppfylt for et bestemt punkt \((x, y)\). For hvert kodeeksempel:

  • Les kodeeksempelet og løs likningssystemet (med valgfri metode) programmet sjekker.

  • Forutsi om programmet skriver ut True eller False.

  • Skriv inn forutsigelsen din og sjekk svaret ditt!

⚠️ Merk at nøkkelordet and = \(\land\) (og samtidig)

⚠️ Merk at nøkkelordet and = \(\land\) (og samtidig)

⚠️ Merk at nøkkelordet and = \(\land\) (og samtidig)

For å få programmet til å si ifra for oss når det finner en løsning, kan vi bruke en if-setning som sjekker om begge likningene er sanne, og deretter skriver ut svaret!

  • Les eksemplene under og kjør programmene.

  • Kan du forklare sammenhengen mellom utskriften og animasjonen?

Programkode

Animasjon

../../../../_images/animasjon_1.gif

Programkode

Animasjon

../../../../_images/animasjon_2.gif

I oppgavene under må du fylle inn programmet med riktig likningssystem i if-setningen for å bestemme løsningen.

Bruk programmet til å bestemme løsningen av likningssystemet

\[ 3x + 2y = 7 \quad \land \quad x - y = 4 \]

Fasit

Programkode:

1for x in range(-5, 6):
2    for y in range(-5, 6):
3        if 3*x + 2*y == 7 and x - y == 4:
4            print(f"{x = } \t {y = }")

som gir utskriften

x = 3 	 y = -1

som betyr at

\[ 3x + 2y = 7 \quad \land \quad x - y = 4 \quad \iff \quad x = 3 \quad \land \quad y = -1 \]

Bruk programmet til å bestemme løsningen av likningssystemet

\[ x + 2y = 4 \quad \land \quad -2x + y = -3 \]

Fasit

Programkode:

1for x in range(-5, 6):
2    for y in range(-5, 6):
3        if x + 2*y == 4 and -2*x + y == -3:
4            print(f"{x = } \t {y = }")

som gir utskriften

x = 2 	 y = 1

som betyr at

\[ x + 2y = 4 \quad \land \quad -2x + y = -3 \quad \iff \quad x = 2 \quad \land \quad y = 1 \]

Bruk programmet til å bestemme løsningen av likningssystemet

\[ 3x + 4y = -10 \quad \land \quad \dfrac{1}{2}x + y = -2 \]

Fasit

Programkode:

1for x in range(-5, 6):
2    for y in range(-5, 6):
3        if 3*x + 4*y == -10 and x/2 + y == -2:
4            print(f"{x = } \t {y = }")

som gir utskriften

x = -2 	 y = -1

som betyr at

\[ 3x + 4y = -10 \quad \land \quad \dfrac{1}{2}x + y = -2 \quad \iff \quad x = -2 \quad \land \quad y = -1 \]

I programmene under må du:

  • Fylle inn likningssystemene i if-setningen.

  • Bestemme riktig range i for-løkkene slik at programmet lager de samme punktene \((x, y)\) som vises i tilhørende animasjonene.

Bruk programmet under til å bestemme løsningen av likningssystemet

\[ x + 3y = 5 \quad \land \quad 2x - y = 3 \]

Programkode

Animasjon

../../../../_images/oppgave_1_animasjon.gif

Fasit

1for x in range(0, 4):
2    for y in range(-2, 3):
3        if x + 3*y == 5 and 2*x - y == 3:
4            print(f"{x = } \t {y = }")

Bruk programmet under til å bestemme løsningen av likningssystemet

\[ x + y = -1 \quad \land \quad x + \dfrac{1}{2}y = \dfrac{1}{2} \]

Programkode

Animasjon

../../../../_images/oppgave_2_animasjon.gif

Fasit

1for x in range(0, 5):
2    for y in range(-4, 1):
3        if x + y == -1 and x + y/2 == 1/2:     
4            print(f"{x = } \t {y = }")

Bruk programmet under til å bestemme løsningen av likningssystemet

\[ 2x - y = -5 \quad \land \quad x + 3y = 1 \]

Programkode

Animasjon

../../../../_images/oppgave_3_animasjon.gif

Fasit

1for x in range(-3, 4): 
2    for y in range(0, 4):
3        if 2*x - y == -5 and x + 3*y == 1:
4            print(f"{x = } \t {y = }")

Utforsk 4: anvendelse

Her skal vi se hvordan vi kan anvende gridsøk til å bestemme funksjonsuttrykket til lineære funksjoner. I dette tilfellet er det ikke lenger \(x\) og \(y\) som er variablene i likningssystemet, men koeffisientene \(a\) og \(b\) til den lineære funksjonen.

I eksemplene under viser vi hvordan vi kan bruke gridsøk til å bestemme koeffisientene \(a\) og \(b\) til en lineær funksjon \(f(x) = ax + b\) som går gjennom to gitte punkter.

  • Les programmene og sjekk at du kan forklare sammenhengen mellom innholdet i programmet og likningene den lineære funksjonen må oppfylle.

  • Bruk utskriften av programmet til å bestemme funksjonsuttrykket til funksjonen.

Et lineær funksjon \(f(x) = ax + b\) går gjennom punktene \((-1, -5)\) og \((1, 1)\). Dette gir likningssystemet

\[ f(-1) = -5 \quad \land \quad f(1) = 1 \]
\[ -a + b = -5 \quad \land \quad a + b = 1 \]

Programkode:

Fasit

\[ f(x) = 3x - 2 \]

En lineær funksjon \(g(x) = ax + b\) går gjennom punktene \((-3, 5)\) og \((-2, 4)\). Dette gir likningssystemet

\[ g(-3) = 5 \quad \land \quad g(-2) = 4 \]
\[ -3a + b = 5 \quad \land \quad -2a + b = 4 \]

Programkode:

Fasit

\[ g(x) = -x + 2 \]

En lineær funksjon \(h(x) = ax + b\) går gjennom punktene \((-2, -5)\) og \((3, 10)\). Dette gir likningssystemet

\[ h(-2) = -5 \quad \land \quad h(3) = 10 \]
\[ -2a + b = -5 \quad \land \quad 3a + b = 10 \]

Programkode:

Fasit

\[ h(x) = 3x + 1 \]

I oppgavene under skal du sette opp likningssystemet for koeffisientene til de lineære funksjonene og fylle inn i programmet for å bestemme funksjonsuttrykket.

En lineær funksjon \(f(x) = ax + b\) går gjennom punktene \((-1, -6)\) og \((3, 10)\).

  1. Sett opp et likningssystem for koeffisientene til \(f\).

  2. Fyll ut programmet under og bruk det til å bestemme \(f(x)\).

Fasit

\[ -a + b = -6 \quad \land \quad 3a + b = 10 \]
1for a in range(-5, 6):
2    for b in range(-5, 6):
3        if -a + b == -6 and 3*a + b == 10:
4            print(f"{a = } \t {b = }")

Utskrift:

a = 4 	 b = -2
\[ f(x) = 4x - 2 \]

En lineær funksjon \(g(x) = ax + b\) går gjennom punktene \((1, 1)\) og \((4, -5)\).

  1. Sett opp et likningssystem for koeffisientene til \(g\).

  2. Fyll ut programmet under og bruk det til å bestemme \(g(x)\).

Fasit

\[ a + b = 1 \quad \land \quad 4a + b = -5 \]
1for a in range(-5, 6):
2    for b in range(-5, 6):
3        if a + b == 1 and 4*a + b == -5:
4            print(f"{a = } \t {b = }")

Utskrift:

a = -2 	 b = 3
\[ g(x) = -2x + 3 \]

En lineær funksjon \(h(x) = ax + b\) går gjennom punktene \((-3, 13)\) og \((7, -17)\).

  1. Sett opp et likningssystem for koeffisientene til \(h\).

  2. Fyll ut programmet under og bruk det til å bestemme \(h(x)\).

Fasit

\[ -3a + b = 13 \quad \land \quad 7a + b = -17 \]
1for a in range(-5, 6):
2    for b in range(-5, 6):
3        if -3*a + b == 13 and 7*a + b == -17:
4            print(f"{a = } \t {b = }")

Utskrift:

a = -3 	 b = 4
\[ h(x) = -3x + 4 \]
Innhold