1.1. De naturlige tallene \(\mathbb{N}\) og heltallene \(\mathbb{Z}\)

Læringsmål

• Kunne beskrive naturlige tall.

• Kunne beskrive partall og oddetall og egenskaper ved disse.

• Kunne bestemme om et tall er et primtall og primtallsfaktorisere et naturlig tall.

Naturlige tall

De naturlige tallene er de positive heltallene \(1, 2, 3, \ldots\), og så videre. Vi bruker symbolet \(\mathbb{N}\) for å betegne alle naturlige tall og kaller det for mengden av de naturlige tallene. Vi kan bruke listenotasjon for å beskrive tallmengden på en enkel måte:

Notasjonen \(\{1, 2, 3, 4, 5, \ldots\}\) kalles for listenotasjon. Det betyr at vi lister opp de første elementene i mengden. Vi bruker “\(\ldots\)” for å vise at mønsteret fortsetter.

De naturlige tallene \(\mathbb{N}\)

De naturlige tallene er de positive heltallene \(1, 2, 3, \ldots\), og så videre. Vi betegner mengden av de naturlige tallene med symbolet \(\mathbb{N}\). Vi skriver

\[ \mathbb{N} = \{1, 2, 3, 4, 5, \ldots\} \]

Hvis et tall \(n\) er et naturlig tall, skriver vi \(n \in \mathbb{N}\) som vi leser som “\(n\) er et element i mengden av naturlige tall”.

Blant de naturlige tallene, kan vi dele dem inn i to mindre mengder: Partall og oddetall. Vi skal se på hvordan vi kan beskrive disse to mengdene.

Partall

Partallene kan listes opp som

\[ \mathrm{partall} = \{2, 4, 6, 8, 10, \ldots\} \]

Et tall er delelig med \(2\) dersom vi får et nytt naturlig tall etter vi har delt det på \(2\). For eksempel er \(6\) delelig med \(2\) fordi \(\dfrac{6}{2} = 3\), og \(3\) er et naturlig tall.

Det vi kan legge merke til er at alle partall er delelige med \(2\). Faktisk er det bare partall som er delelige med \(2\) blant de naturlige tallene.

Underveisoppgave 1

a

Ta utgangspunkt i de naturlige tallene

\[ \mathbb{N} = \{1, 2, 3, 4, 5, \ldots\} \]

og lag en formel \(P(n)\) for partallene uttrykt ved de naturlige tallene \(n \in \mathbb{N}\).
Formelen skal kunne brukes til å lage alle partallene ved hjelp av de naturlige tallene.

Fasit

\[ P(n) = 2 \cdot n \]

b

Hva slags tall får du dersom du plusser sammen to partall?

c

Hva slags tall får du dersom du ganger sammen to partall?

d

Hva slags tall får du dersom du regner ut \(a^2\) der \(a\) er et partall?

Oddetall

Oddetallene kan listes opp som

\[ \mathrm{oddetall} = \{1, 3, 5, 7, 9, \ldots\} \]

Oddetall på en annen side er ikke delelige med \(2\). Beskrivelsen av oddetall kan vi få ved å ta utgangspunkt i beskrivelsen av partall.

Underveisoppgave 2

a

Gang et naturlig tall med \(2\). Hva må du trekke fra for å få det nærmeste oddetallet?

Løsning

For å få det nærmeste oddetallet må vi trekke fra \(1\). Hvis vi for eksempel ganger \(3\) med \(2\), så får vi \(6\). Trekker vi fra \(1\), så får vi \(5\).

b

Kan du lage en generell formel for oddetallene uttrykt ved de naturlige tallene \(n \in \mathbb{N}\)?

Løsning

Oddetallene kan skrives som \(2\cdot n - 1\) der \(n \in \mathbb{N}\).

Primtall

De første primtallene er

\[ 2, 3, 5, 7, 11, 13, 17, 19, 23, \ldots \]

Man har prøvd å finne en generell sammenheng for primtallene helt siden man oppdaget dem. Men det er fortsatt ingen formel for dem, og vi kommer kanskje aldri til å finne en.

Et primtall \(p\) er et naturlig tall som kun er delelig med \(1\) og seg selv. Dette er kjennetegnet på alle primtall. Det finnes ingen generell formel for primtall, så man må sjekke hvert enkelt tall for å finne ut om det er et primtall eller ikke. I oppgavene vil du møte på en strategi du kan bruke for å avgjøre om et tall er et primtall ved å gjøre færrest mulig tester.

Primtallsfaktorisering

Alle naturlige tall kan primtallsfaktoriseres. Det vil si at vi skriver om et naturlig tall som et produkt av primtall. For eksempel har vi

\[ 12 = 2 \cdot 2 \cdot 3 = 2^2 \cdot 3 \]

En oversiktlig strategi for å utføre denne faktoriseringen er å bruke trefaktorisering. Det vil si at vi starter fra et naturlig tall og så lager vi et faktortre der endepunktet til hver gren i treet er en primtallsfaktor i tallet. Nedenfor ser du et eksempel på dette.

Eksempel 1

Vi skal trefaktorisere tallet \(60\). Vi gjør dette ved å dele opp tallet i primtall steg-for-steg fra lavest til størst primtall:

1. Vi begynner med det minste primtallet \(2\). Siden \(60\) er et partall, er det delelig med \(2\). For å få \(60\) må vi gange \(2\) med \(30\). Vi skriver derfor \(30\) i treet som en gren til nedenfor-til-høyre for \(60\).

2. Neste tall er \(30\). Dette er også et partall, så vi kan dele det på \(2\) igjen. Vi får da \(15\) som vi skriver i treet som en gren til nedenfor-til-høyre for \(30\).

3. Nå har vi \(15\). Dette er ikke delelig med \(2\), så vi går videre til neste primtall, som er \(3\). Siden \(15\) er delelig med \(3\), kan vi dele det på \(3\) og få \(5\). Vi skriver dette i treet som en gren til nedenfor-til-høyre for \(15\)

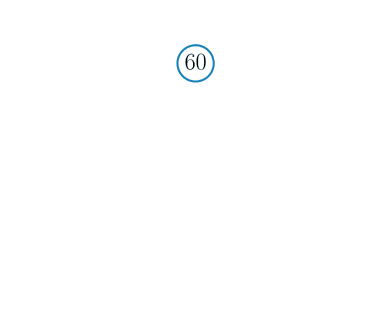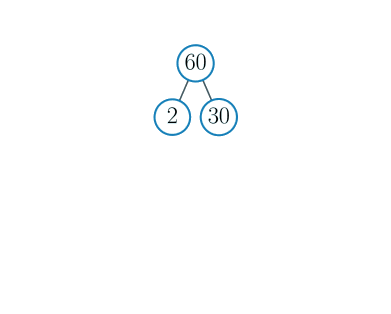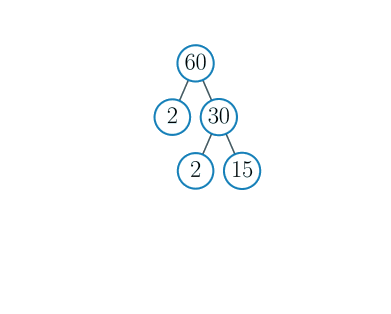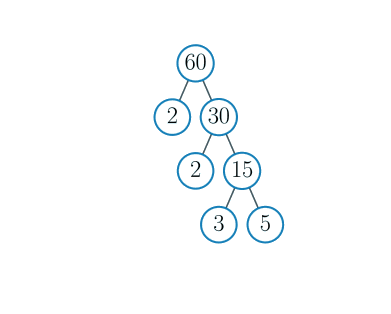
4. Nå har vi bare \(5\) igjen, og dette er et primtall. Vi kan ikke dele det videre, så treet stopper her.

Det ferdigbygde treet er vist til høyre.

I treet vårt til høyre kan vi se at faktorene til \(60\) blir enden på hver gren i treet slik at vi til slutt kan skrive ned

\[ 60 = 2 \cdot 2 \cdot 3 \cdot 5 \]

---

Underveisoppgave 3

Bruk trefaktorisering til å primtallsfaktorisere \(72\).

Løsning

Fra faktortreet til høyre, kan vi primtallsfaktorisere \(72\) som

\[ 72 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \]

Heltallene

Symbolet \(\subset\) leses som “er en delmengde av”.

Heltallene \(\mathbb{Z}\)

Heltallene er alle mulige hele tall og betegnes med symbolet \(\mathbb{Z}\). De kan listes opp som

\[ \mathbb{Z} = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\} \]

Vi kan merke oss at alle de naturlige tallene også er hele tall. Vi skriver derfor at \(\mathbb{N} \subset \mathbb{Z}\), som leses som “mengden av naturlige tall er en delmengde av mengden av hele tall”.